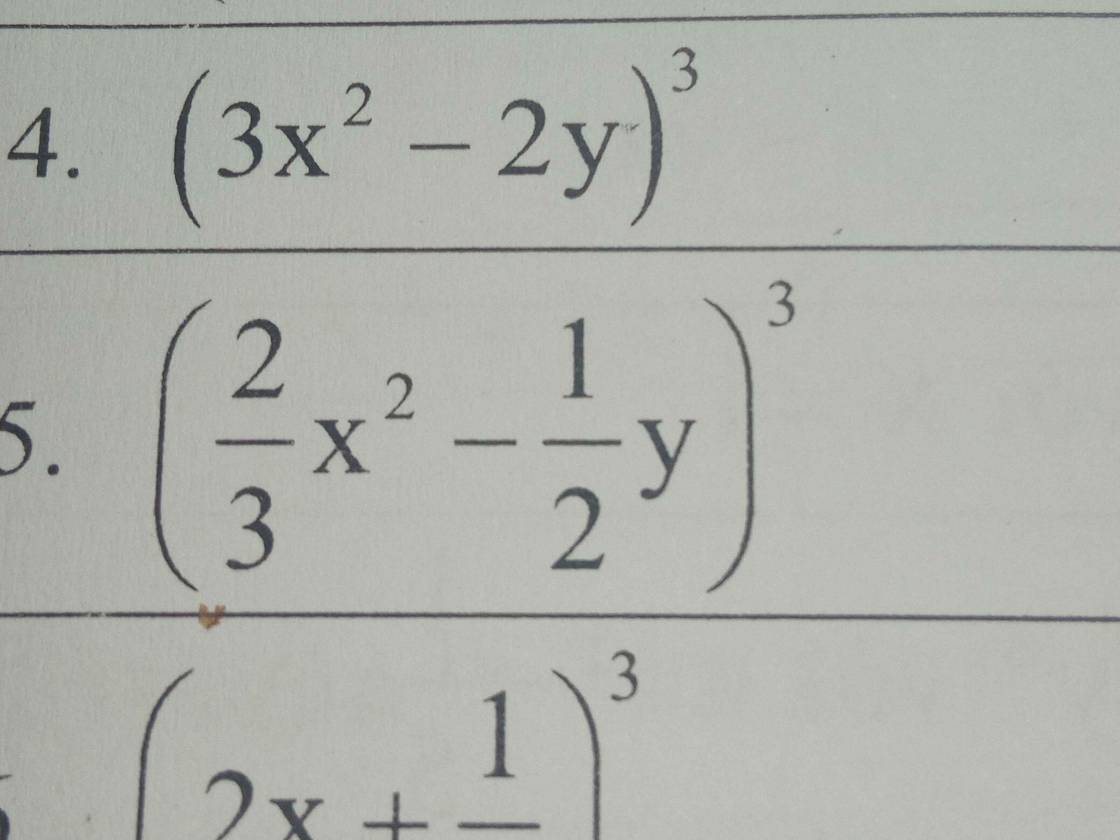giải hộ câu 5nha
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
PD
0
20 tháng 7 2022
Ta có :
\(\dfrac{ab+bc+ca}{xy+yz+zx}=\dfrac{ab}{xy}=\dfrac{bc}{yz}=\dfrac{ca}{zx}\)
\(\Rightarrow\dfrac{a}{x}.\dfrac{b}{y}=\dfrac{b}{y}.\dfrac{c}{z}=\dfrac{c}{z}.\dfrac{a}{x}\)
Mà \(\dfrac{a}{x}=\dfrac{b}{y}=\dfrac{c}{z}\)
\(\Rightarrow\dfrac{a^2}{x^2}=\dfrac{b^2}{y^2}=\dfrac{c^2}{z^2}=\dfrac{a^2+b^2+c^2}{x^2+y^2+z^2}\left(\text{Đ}PCM\right)\)
20 tháng 7 2022
\(ab\left(a^2-b^2\right)+bc\left(b^2-c^2\right)+ca\left(c^2-a^2\right)\)
\(=a^3b-ab^3+b^3c-bc^3+c^3a-ca^3\)
\(=a^3\left(b-c\right)+b^3\left(c-a\right)+c^3\left(a-b\right)\)
\(=a^3\left(b-a+a-c\right)+b^3\left(c-a\right)+c^3\left(a-b\right)\)
\(=\left(a-b\right)\left(c^3-a^3\right)+\left(c-a\right)\left(b^3-a^3\right)\)
\(=\left(a-b\right)\left(c-a\right)\left(c^2+ca+a^2\right)-\left(c-a\right)\left(a-b\right)\left(a^2+ab+b^2\right)\)
\(=\left(a-b\right)\left(c-a\right)\left(c^2+ca+a^2-a^2-ab-b^2\right)\)
\(=\left(a-b\right)\left(c-a\right)\left(c^2+ca-ab-b^2\right)\)
\(=\left(a-b\right)\left(c-a\right)\left[-a\left(b-c\right)-\left(b-c\right)\left(b+c\right)\right]\)
\(=-\left(a-b\right)\left(b-c\right)\left(c-a\right)\left(a+b+c\right)\)
K
3
DT
Dang Tung
CTVHS
19 tháng 7 2022
\(16x^2+8x+100=\left(4x\right)^2+2.4x.1+1^2+99\\ =\left(4x+1\right)^2+99>=99>0\left(DPCM\right)\)
19 tháng 7 2022
\(16x^2+8x+100>0\)
\(\Leftrightarrow\left(4x\right)^2+2.4x.1+1+99>0\)
\(\Leftrightarrow\left(4x+1\right)^2+99>0\left(\forall x\in R\right)\)
2
CC
0
TM
2
19 tháng 7 2022
\(\left(2x+1\right)^2-4.\left(x+2\right)=9\)
\(\Leftrightarrow4x^2+4x+1-4x-8=9\)
\(\Leftrightarrow4x^2=16\)
\(\Leftrightarrow x^2=4\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)
vậy...............
19 tháng 7 2022
\(\left(2x+1\right)^2-4\left(x+2\right)=9\)
\(\Leftrightarrow4x^2+4x+1-4x-8=9\)
\(\Leftrightarrow4x^2-7-9=0\)
\(\Leftrightarrow4x^2-16=0\)
\(\Leftrightarrow x^2=4\)
\(\Leftrightarrow x=\pm2\)