Hình lập phương A có cạnh dài gấp 5 lần hình lập phương B. Thể tích hình lập phương A gấp thể tích hình lập phương B...............lần
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(\dfrac{5}{12}=\dfrac{5\times11}{12\times11}=\dfrac{55}{132}\)
\(\dfrac{6}{11}=\dfrac{6\times12}{11\times12}=\dfrac{72}{132}\)

3 - 4x(25 - 2x) = 8x² + x - 300
3 - 100x + 8x² = 8x² + x - 300
-100x + 8x² - 8x² - x = -300 - 3
-101x = -303
x = -303 : (-101)
x = 3
Vậy S = {3}

ĐKXĐ: \(x\notin\left\{0;3;-3;-\dfrac{3}{2}\right\}\)
\(\dfrac{x^2-6}{x-3}+\dfrac{x^2+3x}{2x+3}\left(\dfrac{x}{x^2-9}-\dfrac{x+3}{x\left(x-3\right)}\right)\)
\(=\dfrac{x^2-6}{x-3}+\dfrac{x\left(x+3\right)}{2x+3}\cdot\left(\dfrac{x}{\left(x-3\right)\left(x+3\right)}-\dfrac{x+3}{x\left(x-3\right)}\right)\)
\(=\dfrac{x^2-6}{x-3}+\dfrac{x\left(x+3\right)}{2x+3}\cdot\dfrac{x^2-\left(x+3\right)^2}{x\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{x^2-6}{x-3}+\dfrac{x^2-x^2-6x-9}{\left(2x+3\right)\left(x-3\right)}\)
\(=\dfrac{x^2-6}{x-3}-\dfrac{3}{x-3}=\dfrac{x^2-9}{x-3}=x+3\)

a: Xét ΔCED vuông tại E và ΔCFD vuông tại F có
CD chung
\(\widehat{ECD}=\widehat{FCD}\)
Do đó: ΔCED=ΔCFD
=>CE=CF: DE=DF
Xét ΔCEK vuông tại E và ΔCFH vuông tại F có
CE=CF
\(\widehat{ECK}\) chung
Do đó: ΔCEK=ΔCFH
b: Xét ΔDEH vuông tại E và ΔDFK vuông tại F có
DE=DF
\(\widehat{EDH}=\widehat{FDK}\)
Do đó: ΔDEH=ΔDFK
=>DH=DK
=>D nằm trên đường trung trực của HK(1)
Ta có: CH=CK
=>C nằm trên đường trung trực của HK(2)
Ta có: MH=MK
=>M nằm trên đường trung trực của HK(3)
Từ (1),(2),(3) suy ra C,D,M thẳng hàng


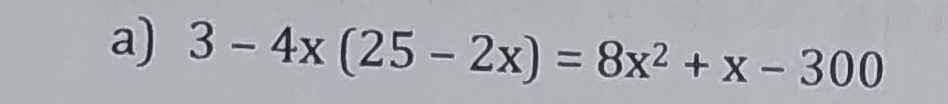
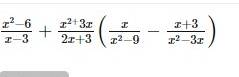 giúp tui zới mn oi bí quá
giúp tui zới mn oi bí quá
Tỉ số giữa thể tích hình lập phương A và hình lập phương B là:
53=125
=>Thể tích hình lập phương A gấp thể tích hình lập phương B là 125 lần