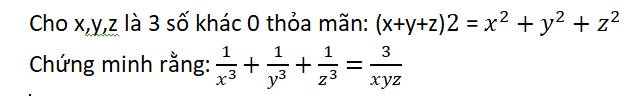mọi người cho mình xin cách giải với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(\left(x+y+z\right)^2=x^2+y^2+z^2\)
\(\Leftrightarrow x^2+y^2+z^2+2xy+2yz+2zx-x^2-y^2-z^2=0\)
\(\Leftrightarrow2\left(xy+yz+zx\right)=0\)
\(\Leftrightarrow xy+yz+zx=0\)
Đặt \(\dfrac{1}{x}=a;\dfrac{1}{y}=b;\dfrac{1}{z}=c\Rightarrow\dfrac{3}{xyz}=3abc\)
Lại có: \(xy+yz+zx=0\Rightarrow\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{ca}=0\)
\(\Leftrightarrow\dfrac{a+b+c}{abc}=0\Leftrightarrow a+b+c=0\)
Khi đó, xét hiệu: \(\dfrac{1}{x^3}+\dfrac{1}{y^3}+\dfrac{1}{z^3}-\dfrac{3}{xyz}\)
\(=a^3+b^3+c^3-3abc\)
\(=\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc\)
\(=\left(a+b+c\right)^3-3\left(a+b\right)c\left(a+b+c\right)-3ab\left(a+b+c\right)\)
\(=0\) (do \(a+b+c=0\))
\(\Rightarrow\dfrac{1}{x^3}+\dfrac{1}{y^3}+\dfrac{1}{z^3}=\dfrac{3}{xyz}\) (đpcm)
\(Toru\)



a: \(\text{Δ}=\left(2m+1\right)^2-4\cdot\left(m^2+\dfrac{1}{2}\right)\)
\(=4m^2+4m+1-4m^2-2=4m-1\)
Để phương trình có hai nghiệm phân biệt thì Δ>0
=>4m-1>0
=>m>1/4
b: Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2m+1\\x_1x_2=\dfrac{c}{a}=m^2+\dfrac{1}{2}\end{matrix}\right.\)
\(M=\left(x_1-1\right)\left(x_2-1\right)\)
\(=x_1x_2-\left(x_1+x_2\right)+1\)
\(=m^2+\dfrac{1}{2}-2m-1+1\)
\(=m^2-2m+\dfrac{1}{2}\)
\(=m^2-2m+1-\dfrac{1}{2}=\left(m-1\right)^2-\dfrac{1}{2}>=-\dfrac{1}{2}\forall m\)
Dấu '=' xảy ra khi m-1=0
=>m=1(nhận