Bài 1:

a, \(\dfrac{2}{3}\) + \(\dfrac{1}{5}\). \(\dfrac{10}{7}\)

= \(\dfrac{2}{3}\) + \(\dfrac{2}{7}\) 

= \(\dfrac{20}{21}\)

b, \(\dfrac{7}{12}\) - \(\dfrac{27}{7}\). \(\dfrac{1}{18}\)

= \(\dfrac{7}{12}\) - \(\dfrac{3}{14}\)

= \(\dfrac{31}{84}\)

c, \(\dfrac{3}{10}\). \(\dfrac{-5}{6}\) - \(\dfrac{1}{8}\)

= - \(\dfrac{1}{4}\) - \(\dfrac{1}{8}\)

= - \(\dfrac{3}{8}\)

d, - \(\dfrac{4}{9}\): \(\dfrac{8}{3}\) + \(\dfrac{1}{18}\)

= - \(\dfrac{1}{6}\) + \(\dfrac{1}{18}\)

= - \(\dfrac{1}{9}\)

e,  {[(\(\dfrac{1}{2}\) - \(\dfrac{2}{3}\))² : 2 ] - 1}. \(\dfrac{4}{5}\)

= {[ (-\(\dfrac{1}{6}\))² : 2] - 1}. \(\dfrac{4}{5}\)

= { [\(\dfrac{1}{36}\) : 2] - 1}. \(\dfrac{4}{5}\)

= { \(\dfrac{1}{72}\) - 1}. \(\dfrac{4}{5}\)

=- \(\dfrac{71}{72}\).\(\dfrac{4}{5}\)

= -\(\dfrac{71}{90}\)

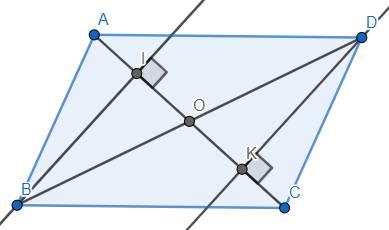
b) Vì BI vuông góc với AC tại I, nên I thuộc AC.

    Vì DK vuông góc với AC tại K, nên K thuộc AC.

    Vì O là giao điểm của AC và BD nên O thuộc AC.

    Suy ra I, O, K là các điểm thuộc AC; từ đó ba điểm I, O, K thẳng hàng

 \(2.\left(x^2+\dfrac{1}{2}y\right)\left(2x^2-y\right)\)

\(=\left(2x^2+y\right)\left(2x^2-y\right)\)

\(=\left(2x^2\right)^2-y^2\)    Ta sử dụng \(\left[\left(a-b\right)\left(a+b\right)=a^2-b^2\right]\)

\(=2^2\left(x^2\right)^2-y^2\)

\(=2^2x^4-y^2\)

\(=4x^4-y^2\)

Vậy khai triển của biểu thức \(2.\left(2x^2+\dfrac{1}{2}y\right)\left(2x^2-y\right)\) là: \(4x^4-y^2\)

\(2\left(x^2+\dfrac{1}{2}\right)\left(2x^2-y\right)\)

\(=2.2.\left(x^2+\dfrac{1}{2}\right)\left(x^2-\dfrac{1}{2}\right)\)

\(=4.\left(x^4-\dfrac{1}{4}\right)\)

a,(0,8)⁵:(0,4)⁶ = (\(\dfrac{0,8}{0,4}\))⁵ : 0,4 = 2⁵:0,4 = 80

b, (-25)⁷: 32³ - \(\dfrac{6103515625}{3276}\) = - 186264,5149

c, \(\dfrac{4^2.4^3}{2^{10}}\) = \(\dfrac{4^5}{2^{10}}\) = \(\dfrac{2^{10}}{2^{10}}\) = 1

d, \(\dfrac{9^5.5^7}{45^7}\) = \(\dfrac{9^5.5^7}{9^7.5^7}\) = \(\dfrac{1}{81}\)

\(\dfrac{\left(0.8\right)^5}{\left(0.4\right)^4}\)=\(\dfrac{\left(2.0,4\right)^5}{\left(0.4^4\right)}\)=\(\dfrac{2^5.\left(0.4\right)^5}{\left(0,4\right)^4}\)=\(2^5\).\(\left(0.4\right)^1\)=12,8

b)câu b không biết có sai đề không nhưng đáp án câu b là -186264,5149

c) \(\dfrac{4^2.4^3}{2^{10}}\)=\(\dfrac{4^5}{\left(2^2\right)^5}\)=\(\dfrac{4^5}{4^5}\)=1

d)\(\dfrac{9^5.5^7}{45^7}\)=\(\dfrac{9^5.5^5.5^2}{45^7}\)=\(\dfrac{45^5.5^2}{45^7}\)=\(\dfrac{5^2}{45^2}\)=\(\left(\dfrac{5}{45}\right)^2\)=\(\left(\dfrac{1}{9}\right)^2\)=\(\dfrac{1}{81}\)

Hôm nay olm.vn sẽ hướng dẫn các em cách giải phương trình nghiệm nguyên bằng nguyên lí kẹp. Cấu trúc đề thi hsg, thi chuyên thi violympic.

         (3n + 1)² =  9n² + 2n + 1 < 9n² + 3n + 4 \(\forall\) n \(\in\) N (1)

        (3n + 2)² =   (3n + 2).(3n +2) = 9n² + 12n + 4

 ⇒(3n + 2)²  ≥  9n² + 3n + 4 \(\forall\) n \(\in\) N (2)

Kết hợp (1) và (2) ta có: (3n +1)² < 9n² + 3n + 4 ≤ (3n + 2)²

 Vì (3n + 1)² và (3n +2)² là hai số chính phương liên tiếp nên 

9n² + 3n + 4 là số chính phương khi và chỉ khi:

 9n² + 3n + 4 = (3n + 2)²  ⇒ 9n² + 3n + 4 = 9n² + 12n + 4

 9n² + 12n + 4 - 9n² - 3n - 4 =  9n = 0 ⇒ n = 0

Vậy với n = 0 thì 9n² + 3n + 4 là  số chính phương.

\(A=\sqrt[]{1+2+3+...+\left(n-1\right)+n+...+3+2+1}\)

Ta có :

\(1+2+3+...+\left(n-1\right)=\left(n-1\right)+...+3+2+1=\left[\left(n-1\right)-1\right]+1\left(n-1+1\right):2\)

\(=\dfrac{\left(n-1\right)n}{2}\)

\(\Rightarrow A=\sqrt[]{\dfrac{\left(n-1\right)n}{2}.2+n}\)

\(\Rightarrow A=\sqrt[]{\left(n-1\right)n+n}\)

\(\Rightarrow A=\sqrt[]{n^2-n+n}\)

\(\Rightarrow A=\sqrt[]{n^2}\)

\(\Rightarrow A=n\left(n>0\right)\)

\(\Rightarrow dpcm\)

mơn trí

   (2\(x\) + 3y)²

= (2\(x\) + 3y).(2\(x\) + 3y)

= 4\(x\)² + 6\(xy\) + 6\(xy\) + 9y²

= 4\(x^2\) + 12\(xy\) + 9y²

\(4x^2+12xy+9y^2\)

(2x - 1)⁸ = (2x - 1)¹⁰

(2x - 1)¹⁰ - (2x - 1)⁸ = 0

(2x - 1)⁸.[(2x - 1)² - 1] = 0

(2x - 1)⁸ = 0 hoặc (2x - 1)² - 1 = 0

*) (2x - 1)⁸ = 0

2x - 1 = 0

2x = 1

x = 1/2

*) (2x - 1)² - 1 = 0

(2x - 1)² = 1

2x - 1 = 1 hoặc 2x - 1 = -1

**) 2x - 1 = 1

2x = 2

x = 1

**) 2x - 1 = -1

2x = 0

x = 0

Vậy x = 0; x = 1/2; x = 1

(2x - 1)⁸ = (2x - 1)¹⁰

=) (2x - 1)¹⁰ : (2x - 1)⁸ = 1

    (2x - 1)² = 1 =) = 1²

=) 2x - 1 = 1

    2x = 2

      x = 1.

Lời giải:

\(\overline{0,x(y)}+\overline{0,y(x)}=\overline{0,x}+\overline{0,y}+\overline{0,0(y)}+\overline{0,0(x)}\)

\(=(x+y).0,1+\frac{y}{90}+\frac{x}{90}=(x+y).0,1+(x+y).\frac{1}{90}=9.0,1+9.\frac{1}{90}=1\)

em cảm ơn Akai Haruma 

   (\(x\) - 3).(3 + \(x\)) 

= 3\(x\) + \(x^2\) - 9 - 3\(x\)

= \(x^2\) - 9 

\(\left(x-3\right)\left(3+x\right)\\ =\left(x-3\right).3+\left(x-3\right).x\\ =3x-9+2x-3x\\ =3x-9-x\\ =3x-x+9\\ =2x+9.\)