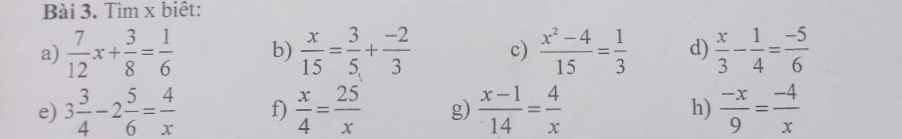 giup em bai nay
giup em bai nay
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: 36p=0,6 giờ
Sau 0,6 giờ, xe máy đi được:
35x0,6=21(km)
Hiệu vận tốc hai xe là 50-35=15(km/h)
Hai xe gặp nhau sau khi ô tô đi được:
21:15=1,4(giờ)
b: Nơi gặp nhau cách A:
1,4x50=70(km)



Ta có: \(\left(x+y+z\right)^2=x^2+y^2+z^2\)
\(\Leftrightarrow x^2+y^2+z^2+2xy+2yz+2zx-x^2-y^2-z^2=0\)
\(\Leftrightarrow2\left(xy+yz+zx\right)=0\)
\(\Leftrightarrow xy+yz+zx=0\)
Đặt \(\dfrac{1}{x}=a;\dfrac{1}{y}=b;\dfrac{1}{z}=c\Rightarrow\dfrac{3}{xyz}=3abc\)
Lại có: \(xy+yz+zx=0\Rightarrow\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{ca}=0\)
\(\Leftrightarrow\dfrac{a+b+c}{abc}=0\Leftrightarrow a+b+c=0\)
Khi đó, xét hiệu: \(\dfrac{1}{x^3}+\dfrac{1}{y^3}+\dfrac{1}{z^3}-\dfrac{3}{xyz}\)
\(=a^3+b^3+c^3-3abc\)
\(=\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc\)
\(=\left(a+b+c\right)^3-3\left(a+b\right)c\left(a+b+c\right)-3ab\left(a+b+c\right)\)
\(=0\) (do \(a+b+c=0\))
\(\Rightarrow\dfrac{1}{x^3}+\dfrac{1}{y^3}+\dfrac{1}{z^3}=\dfrac{3}{xyz}\) (đpcm)
\(Toru\)


0,87 : 0,2 + 0,87 × 9 - 0,87 : 0,25
= 0,87 × 5 + 0,87 × 9 - 0,87 × 4
= 0,87 × (5 + 9 - 4)
= 0,87 × 10
= 8,7

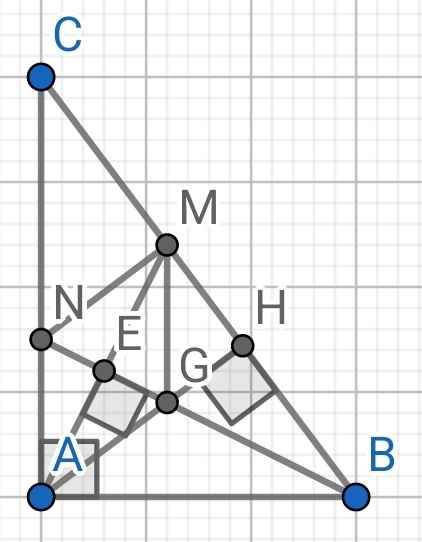
a) Xét hai tam giác vuông: ∆ABE và ∆MBE có:
BA = BM (gt)
BE là cạnh chung
⇒ ∆ABE = ∆MBE (cạnh huyền - cạnh góc vuông)
b) Do ∆ABE = ∆MBE (cmt)
⇒ ∠ABE = ∠MBE (hai góc tương ứng)
⇒ ∠ABN = ∠MBN
Xét ∆ABN và ∆MBN có:
BA = BM (gt)
∠ABN = ∠MBN (cmt)
BN là cạnh chung
⇒ ∆ABN = ∆MBN (c-g-c)
⇒ AN = MN (hai cạnh tương ứng)
c) Do ∆ABN = ∆MBN (cmt)
⇒ ∠BAN = ∠BMN (hai góc tương ứng)
Mà ∠BAN = ∠BAC = 90⁰ (∆ABC vuông tại A)
⇒ ∠BMN = 90⁰
⇒ MN ⊥ BM
⇒ MN ⊥ BC
Lại có AH là đường cao của ∆ABC (gt)
⇒ AH ⊥ BC
Mà MN ⊥ BC (cmt)
⇒ AH // MN
⇒ ∠MGN = ∠ANG (so le trong)


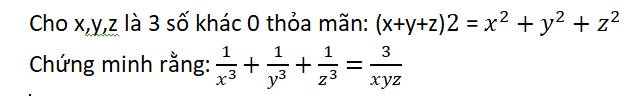
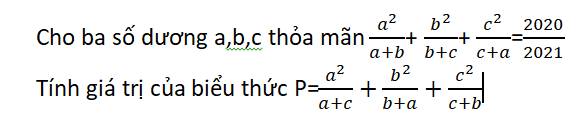
a: \(\dfrac{7}{12}x+\dfrac{3}{8}=\dfrac{1}{6}\)
=>\(\dfrac{7}{12}x=\dfrac{1}{6}-\dfrac{3}{8}=\dfrac{4}{24}-\dfrac{9}{24}=-\dfrac{5}{24}\)
=>\(x=-\dfrac{5}{24}:\dfrac{7}{12}=-\dfrac{5}{24}\cdot\dfrac{12}{7}=\dfrac{-5}{14}\)
b: \(\dfrac{x}{15}=\dfrac{3}{5}+\dfrac{-2}{3}\)
=>\(\dfrac{x}{15}=\dfrac{9}{15}-\dfrac{10}{15}=-\dfrac{1}{15}\)
=>x=-1
c: \(\dfrac{x^2-4}{15}=\dfrac{1}{3}\)
=>\(x^2-4=\dfrac{15}{3}=5\)
=>\(x^2=9\)
=>\(x\in\left\{3;-3\right\}\)
d: \(\dfrac{x}{3}-\dfrac{1}{4}=-\dfrac{5}{6}\)
=>\(\dfrac{x}{3}=\dfrac{1}{4}+\dfrac{-5}{6}=\dfrac{3}{12}-\dfrac{10}{12}=-\dfrac{7}{12}\)
=>\(x=-\dfrac{7}{12}\cdot3=-\dfrac{7}{4}\)
e: \(3\dfrac{3}{4}-2\dfrac{5}{6}=\dfrac{4}{x}\)
=>\(\dfrac{4}{x}=\dfrac{15}{4}-\dfrac{17}{6}=\dfrac{45}{12}-\dfrac{34}{12}=\dfrac{11}{12}\)
=>\(x=4\cdot\dfrac{12}{11}=\dfrac{48}{11}\)
f: ĐKXĐ: x<>0
\(\dfrac{x}{4}=\dfrac{25}{x}\)
=>\(x^2=25\cdot4=100\)
=>\(\left[{}\begin{matrix}x=10\left(nhận\right)\\x=-10\left(nhận\right)\end{matrix}\right.\)
g: ĐKXĐ: x<>0
\(\dfrac{x-1}{14}=\dfrac{4}{x}\)
=>\(x\left(x-1\right)=14\cdot4=56\)
=>\(x^2-x-56=0\)
=>(x-8)(x+7)=0
=>\(\left[{}\begin{matrix}x=8\left(nhận\right)\\x=-7\left(nhận\right)\end{matrix}\right.\)
h: ĐKXĐ: x<>0
\(\dfrac{-x}{9}=\dfrac{-4}{x}\)
=>\(x^2=4\cdot9=36\)
=>\(\left[{}\begin{matrix}x=6\left(nhận\right)\\x=-6\left(nhận\right)\end{matrix}\right.\)