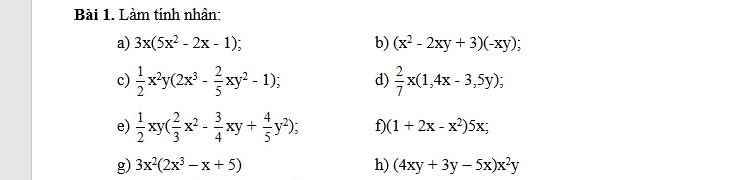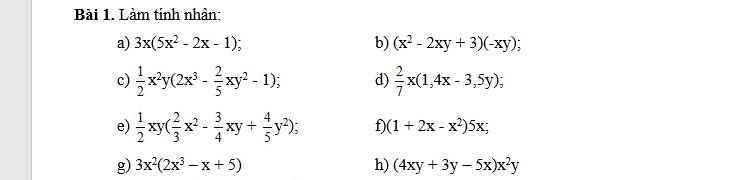\(A=x^2+y^2+2xy+5x+5y-10\\ =\left(x+y\right)^2+5\left(x+y\right)-10\\ =\left(x+y\right)\left(x+y+5\right)-10\\ =2.\left(2+5\right)-10=4\\ \)

\( B=x^3+y^3-6xy\\ =\left(x^3+3x^2y+3xy^2+y^3\right)-\left(3x^2y+3xy^2+6xy\right)\\ =\left(x+y\right)^3-3xy\left(x+y+2\right)\\ =2^3-3xy.4=8-12xy\)

Cái cuối cùng là 2015 nha mn giúp mik vs 

\(a^3+b^3+c^3=3abc\)

\(\Leftrightarrow a^3+b^3+c^3-3abc=0\)

\(\Leftrightarrow\left(a+b\right)^3-3ab\left(a+b\right)+c^3-3abc=0\)

\(\Leftrightarrow\left(a+b+c\right)^3-3c\left(a+b\right)\left(a+b+c\right)-3ab\left(a+b+c\right)=0\)

\(\Leftrightarrow\left(a+b+c\right)\left[\left(a+b+c\right)^2-3ab-3bc-3ac\right]=0\)

\(\Leftrightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)=0\)

\(\Leftrightarrow\left(a+b+c\right)\left[\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\right]=0\)

mà \(a,b,c\) là các số dương nên 

\(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0\)

\(\Leftrightarrow a=b=c\).

Do đó \(M=0\).

Mik nhờ bạn đã trl câu hỏi của mik nhắn tin cho mim hoặc đăng lại lời giải giúp mik đc k lời giải k hiển thị

\(\dfrac{1}{x}+\dfrac{1}{y}>=\dfrac{4}{x+y}\left(2\right)< =>\left(x+y\right)\left(\dfrac{1}{x}+\dfrac{1}{y}\right)>=4\\ < =>1+\dfrac{x}{y}+\dfrac{y}{x}+1>=4\\ < =>\dfrac{x}{y}+\dfrac{y}{x}>=2\left(1\right)\)

Theo BĐT Cô Si, ta có :

\(\dfrac{x}{y}+\dfrac{y}{x}>=2\sqrt{\dfrac{x}{y}.\dfrac{y}{x}}=2\sqrt{1}=2\)

Dấu ''='' xảy ra khi : \(\dfrac{x}{y}=\dfrac{y}{x}< =>x=y\)

=> (1) luôn đúng =>(2) luôn đúng

Vậy \(\dfrac{1}{x}+\dfrac{1}{y}>=\dfrac{4}{x+y}\)( Dấu ''='' xảy ra khi `x=y`)

``

\(P=\dfrac{1}{4x^2+9y^2}+\dfrac{1}{12xy}>=\dfrac{4}{4x^2+9y^2+12xy}=\dfrac{4}{\left(2x+3y\right)^2}=\dfrac{4}{2^2}=1\)

Dấu ''='' xảy ra khi : \(\dfrac{1}{4x^2+9y^2}=\dfrac{1}{12xy};2x+3y=2< =>x=\dfrac{1}{2};y=\dfrac{1}{3}\)