\(\dfrac{\text{3}}{\text{x-5}}\)=\(\dfrac{-4}{\text{x+2}}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(\dfrac{2}{7}=\dfrac{16}{1-5x}\)
=>\(1-5x=16\cdot\dfrac{7}{2}=56\)
=>5x=1-56=-55
=>\(x=-\dfrac{55}{5}=-11\)

\(x+4⋮x-1\)
=>\(x-1+5⋮x-1\)
=>\(5⋮x-1\)
=>\(x-1\in\left\{1;-1;5;-5\right\}\)
=>\(x\in\left\{2;0;6;-4\right\}\)

Bài 6:
Số đường thẳng là: \(4\cdot\dfrac{3}{2}=2\cdot3=6\left(đường\right)\)
Cứ 1 điểm sẽ tạo với 4 - 1 điểm còn lại 4 - 1 tia
Với 4 điểm ta sẽ tạo được số tia là:
(4 - 1) x 3 = 12 (tia)
Kết luận có 12 tia có gốc là một trong 4 điểm đã cho đó lần lượt là các tia:
EF; EG; EH; FE; FG; FH; GE; GF; GH; HE; HF; HG

\(2\dfrac{2}{3}+\left(-\dfrac{5}{8}-2\dfrac{2}{3}\right)\)
\(=\dfrac{8}{3}-\dfrac{5}{8}-\dfrac{8}{3}\)
\(=-\dfrac{5}{8}\)

Nếu trong 50 điểm trên có 5 điểm thẳng hàng, thì ta có:
Lấy 1 điểm bất kì trong năm đường thẳng đó nối với các điểm còn lại, ta có: 4 đường thẳng. Làm như vậy với 4 điểm còn lại, ta có: (4.4)+ 4 = 20 đường thẳng. Nhưng dễ tháy các đường thẳng đã bị lạp lại nên ta có: 20:2=10 đường thẳng. Mà có 5 điểm thẳng hàng nên:
=> Ta có :10-1=9 đường thẳng.
Vậy số đường thẳng có là: 1225-9=1216 đường thẳng.

Các số nguyên có 2 chữ số là: \(-99;-98;...;98;99\)
\(\Rightarrow x=\left(-99\right)+\left(-98\right)+...+98+99=0\)
Số nguyên âm lớn nhất là: - 1
\(\Rightarrow y=-1\)
\(A=2023x^{2022}-2022y^{2023}\)
\(=2023\cdot0^{2022}-2022\cdot\left(-1\right)^{2023}\)
\(=2023\cdot0-2022\cdot\left(-1\right)\)
\(=0+2022\)
\(=2022\)

a: \(1-\dfrac{1}{3}-\dfrac{1}{6}-\dfrac{1}{10}-\dfrac{1}{15}\)
\(=\dfrac{30-10-5-3-2}{30}\)
\(=\dfrac{10}{30}=\dfrac{1}{3}\)
b: \(\dfrac{8}{9}-\dfrac{1}{72}-\dfrac{1}{56}-\dfrac{1}{42}-\dfrac{1}{30}-\dfrac{1}{20}-\dfrac{1}{12}-\dfrac{1}{6}-\dfrac{1}{2}\)
\(=\dfrac{8}{9}-\left(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{8\cdot9}\right)\)
\(=\dfrac{8}{9}-\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{8}-\dfrac{1}{9}\right)\)
\(=\dfrac{8}{9}-\left(1-\dfrac{1}{9}\right)=0\)
c: \(\left(-\dfrac{1}{2}\right)-\left(-\dfrac{3}{5}\right)+\left(-\dfrac{1}{9}\right)+\dfrac{1}{27}-\left(+\dfrac{7}{18}\right)+\dfrac{4}{35}-\left(-\dfrac{2}{7}\right)\)
\(=\dfrac{-1}{2}+\dfrac{3}{5}+\dfrac{-1}{9}+\dfrac{1}{27}-\dfrac{7}{18}+\dfrac{4}{35}+\dfrac{2}{7}\)
\(=\left(\dfrac{3}{5}+\dfrac{4}{35}+\dfrac{2}{7}\right)+\left(-\dfrac{1}{2}-\dfrac{1}{9}-\dfrac{7}{18}\right)+\dfrac{1}{27}\)
\(=\dfrac{21+4+10}{35}+\dfrac{-9-2-7}{18}+\dfrac{1}{27}\)
\(=\dfrac{35}{35}-\dfrac{18}{18}+\dfrac{1}{27}=\dfrac{1}{27}\)
d: \(\dfrac{3}{5}+\dfrac{3}{11}-\left(-\dfrac{3}{7}\right)+\left(\dfrac{2}{17}\right)-\dfrac{1}{35}-\dfrac{3}{4}+\left(-\dfrac{23}{44}\right)\)
\(=\left(\dfrac{3}{5}+\dfrac{3}{7}-\dfrac{1}{35}\right)+\left(\dfrac{3}{11}-\dfrac{3}{4}-\dfrac{23}{44}\right)+\dfrac{2}{17}\)
\(=\dfrac{21+15-1}{35}+\dfrac{12-33-23}{44}+\dfrac{2}{17}\)
\(=\dfrac{35}{35}-\dfrac{44}{44}+\dfrac{2}{17}=\dfrac{2}{17}\)
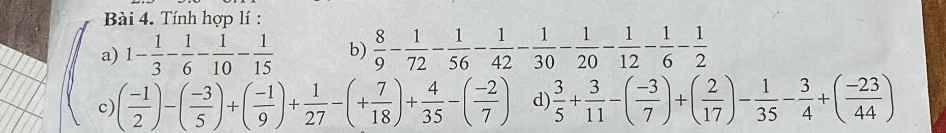
ĐKXĐ: \(x\notin\left\{5;-2\right\}\)
\(\dfrac{3}{x-5}=\dfrac{-4}{x+2}\)
=>-4(x-5)=3(x+2)
=>-4x+20=3x+6
=>-7x=-14
=>x=2(nhận)