Trên cùng 1 nửa mặt phẳng bờ chứa tia Ox , vẽ hai tia Oy và Oz sao cho xOy=135 độ , xOz =45 độ . Chứng tỏ rằng yOz = 90 độ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
Ta có dãy số 2, 4, 6, ..., 2n là một dãy số chẵn liên tiếp.
Ta có công thức tổng của dãy số chẵn liên tiếp là: S = (a1 + an) * n / 2
Với a1 là số đầu tiên của dãy, an là số cuối cùng của dãy, n là số phần tử của dãy.
Áp dụng công thức trên vào bài toán, ta có:
(2 + 2n) * n / 2 = 756
(2n + 2) * n = 1512
2n^2 + 2n = 1512
2n^2 + 2n - 1512 = 0
Giải phương trình trên, ta được n = 18 hoặc n = -19.
Vì n là số tự nhiên nên n = 18.
Vậy số tự nhiên n cần tìm là 18.
Bài 2:
Ta có p = (n - 2)(n^2 + n - 5)
Để p là số nguyên tố, ta có hai trường hợp:
1. n - 2 = 1 và n^2 + n - 5 = p
2. n - 2 = p và n^2 + n - 5 = 1
Xét trường hợp 1:
n - 2 = 1
=> n = 3
Thay n = 3 vào phương trình n^2 + n - 5 = p, ta có:
3^2 + 3 - 5 = p
9 + 3 - 5 = p
7 = p
Vậy n = 3 và p = 7 là một cặp số nguyên tố thỏa mãn.
Xét trường hợp 2:
n - 2 = p
=> n = p + 2
Thay n = p + 2 vào phương trình n^2 + n - 5 = 1, ta có:
(p + 2)^2 + (p + 2) - 5 = 1
p^2 + 4p + 4 + p + 2 - 5 = 1
p^2 + 5p + 1 = 1
p^2 + 5p = 0
p(p + 5) = 0
p = 0 hoặc p = -5
Vì p là số nguyên tố nên p không thể bằng 0 hoặc âm.
Vậy không có số tự nhiên n thỏa mãn trong trường hợp này.
Vậy số tự nhiên n cần tìm là 3.
Bài 1
...=((2n-2):2+1):2=756
(2(n-1):2+1)=756×2
n-1+1=1512
n=1512

nếu p = 2 thì 7p + 9 = 14 + 9 = 23 (thỏa mãn)
Nếu p>2 vì p là số nguyên tố nên p là số lẻ vậy p = 2k + 1 (k\(\in\)N)
⇒ 7p + 9 = 7.(2k+1) + 9 = 14k + 7+ 9 = 14k + 16 ⋮ 2 (loại)
Vậy p = 2

DT ban đầu là S1, DT sau khi mở rộng đáy là S2.
Ta có: S2 = S1 + 10.2 (1)
Với tam giác có đáy là 14cm, ta có: S1 = (14 * h) / 2 (2)
Sau khi mở rộng đáy thêm 3cm, ta có: S2 = ((14 + 3) * h') / 2 (3)
Từ (2) và (3), ta có: S2 = (17 * h') / 2 (4)
Từ (1) và (4), ta có: (17 * h') / 2 = (14 * h) / 2 + 10.2
Rút gọn phương trình, ta được:
17 * h' = 14 * h + 20,4
17h' = 14h + 20,4
17h' - 14h = 20,4
3h' = 20,4
h' = 20,4 / 3
h' = 6,8
Thay giá trị của h' vào phương trình (4), ta được:
S2 = (17 * 6,8) / 2
S2 = 57,8
Thay giá trị của S2 vào phương trình (1), ta được:
57,8 = S1 + 10,2
S1 = 57,8 - 10,2
S1 = 47,6
Vậy DT ban đầu là 47,6 cm2.
...
Nửa chu vi HHCN là:
108,8 : 2 =54,4 (dm)
Ta có sơ đồ :
CD:---------- ---------- ---------- ---------- ----------
Tổng:54,4 dm
CR:---------- ---------- ----------
Chiều dài HHCN là:
54,4 : (3+5)*5=34(dm)
Chiều rộng HHCN là:
54.4-34=20,4(dm)
S xung quanh HHCN là:
(34+20,4)*2*10=1088(dm2)
S 2 mặt đáy là:
(34+20,4)*2=108,8(dm2)
s toàn phần HHCN là:
1088+108,8=1196.8(dm2)
Thể tích HHCN là:
1088*108,8*10=1183744(dm3)
Đ/S:.......
CHÚC BẠN HỌC TỐT!

1) x : \(\left(\dfrac{3}{5}\right)^3\)= \(\dfrac{3}{5}\)
x = \(\dfrac{3}{5}\) x \(\left(\dfrac{3}{5}\right)^3\)
x = \(\left(\dfrac{3}{5}\right)^4\)
2) \(\left(\dfrac{4}{7}\right)^{4^{ }}\). x = \(\left(\dfrac{4}{7}\right)^2\)
x = \(\left(\dfrac{4}{7}\right)^2\):\(\left(\dfrac{4}{7}\right)^4\)
x = \(\dfrac{4^2}{7^2}\) . \(\dfrac{7^4}{4^4}\)
x = \(\dfrac{7^2}{4^2}\)
x = \(\left(\dfrac{7}{4}\right)^2\)
3) (\(\dfrac{2}{5}\) - 3x)2 = \(\dfrac{9}{25}\)
(\(\dfrac{2}{5}\) - 3x)2 = \(\left(\dfrac{3}{5}\right)^2\)= \(\left(-\dfrac{3}{5}\right)^2\)
TH1 : TH2 :
(\(\dfrac{2}{5}\) - 3x)2 = \(\left(\dfrac{3}{5}\right)^2\) (\(\dfrac{2}{5}\) - 3x)2 = \(\left(-\dfrac{3}{5}\right)^2\)
\(\dfrac{2}{5}\) - 3x = \(\dfrac{3}{5}\) \(\dfrac{2}{5}\) - 3x = -\(\dfrac{3}{5}\)
3x = \(\dfrac{2}{5}-\dfrac{3}{5}\) 3x = \(\dfrac{2}{5}\) + \(\dfrac{3}{5}\)
x = \(-\dfrac{1}{5}\) : 3 x = \(\dfrac{5}{5}\) : 3
x = \(-\dfrac{1}{5}\) x \(\dfrac{1}{3}\) x = 1 : 3
x = -\(\dfrac{1}{15}\) x = \(\dfrac{1}{3}\)

DT ban đầu là S1, DT sau khi mở rộng đáy là S2.
Ta có: S2 = S1 + 10.2 (1)
Với tam giác có đáy là 14cm, ta có: S1 = (14 * h) / 2 (2)
Sau khi mở rộng đáy thêm 3cm, ta có: S2 = ((14 + 3) * h') / 2 (3)
Từ (2) và (3), ta có: S2 = (17 * h') / 2 (4)
Từ (1) và (4), ta có: (17 * h') / 2 = (14 * h) / 2 + 10.2
Rút gọn phương trình, ta được:
17 * h' = 14 * h + 20,4
17h' = 14h + 20,4
17h' - 14h = 20,4
3h' = 20,4
h' = 20,4 / 3
h' = 6,8
Thay giá trị của h' vào phương trình (4), ta được:
S2 = (17 * 6,8) / 2
S2 = 57,8
Thay giá trị của S2 vào phương trình (1), ta được:
57,8 = S1 + 10,2
S1 = 57,8 - 10,2
S1 = 47,6
Vậy DT ban đầu là 47,6 cm2.DT ban đầu là S1, DT sau khi mở rộng đáy là S2.
Ta có: S2 = S1 + 10.2 (1)
Với tam giác có đáy là 14cm, ta có: S1 = (14 * h) / 2 (2)
Sau khi mở rộng đáy thêm 3cm, ta có: S2 = ((14 + 3) * h') / 2 (3)
Từ (2) và (3), ta có: S2 = (17 * h') / 2 (4)
Từ (1) và (4), ta có: (17 * h') / 2 = (14 * h) / 2 + 10.2
Rút gọn phương trình, ta được:
17 * h' = 14 * h + 20,4
17h' = 14h + 20,4
17h' - 14h = 20,4
3h' = 20,4
h' = 20,4 / 3
h' = 6,8
Thay giá trị của h' vào phương trình (4), ta được:
S2 = (17 * 6,8) / 2
S2 = 57,8
Thay giá trị của S2 vào phương trình (1), ta được:
57,8 = S1 + 10,2
S1 = 57,8 - 10,2
S1 = 47,6
Vậy DT ban đầu là 47,6 cm2.
Chiều cao ban đầu của tam giác là: 10,2 x 2 : 3 = 6,8 (cm)
Diện tích ban đầu của ta giác là: 14 \(\times\) 6,8: 2 = 47,6 (cm2)
Đáp số:....

Name width of the headers is x (cm).
Theo đề bài, chu vi của chấm là gấp 5 lần chiều rộng, ta có:
2(x + chiều dài) = 5x
2 chiều dài = 3x
chiều dài = 3x/2
Nếu tăng chiều rộng thêm 9 cm và chiều dài thêm 4 cm, ta có:
(x + 9) = (3x/2 + 4)
2x + 18 = 3x + 8
x = 10
Do đó chiều rộng ban đầu của khe cắm là 10 cm.
Diện tích miếng dán ban đầu là:
Diện tích = chiều dài x chiều rộng
Diện tích = (3x/2) x x
Diện tích = (3/2) x 10 x 10
Diện tích = 150 cm²

- 1,257 ; 1,275 ; 1.527 ; 1,572 ; 1,725 ; 1,752.
- 2,175 ; 2,157 ; 2,527 ; 2,572 ; 2,752 ; 2,725.
- 5,127 ; 5,172 ; 5,271 ; 5,217 ; 5,712 ; 5,721.
- 7,125 ; 7,152 ; 7,215 ; 7,251 ; 7,512 ; 7,521.
1.234;1.235;1.237;2.134;2.135;2.137;5.124;5.127;5.147;7.124;7.125;
7.145

Tuổi bà hơn tuổi Lan là: 94 - 40 = 54
Ta có sơ đồ:
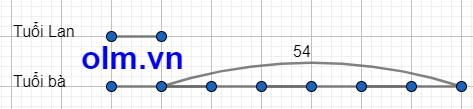
Theo sơ đồ ta có:
Tuổi Lan là: 54 : (7-1) = 9 (tuổi)
Tuổi bà là: 9 \(\times\) 7 = 63 (tuổi)
Tuổi mẹ Lan là: 40 - 9 = 31(tuổi)
Đáp số: ...
Ta có: \(\widehat{xOy}=135^o>\widehat{xOz}=45^o\)
⇒ Tia Oz nằm giữa tia Ox và tia Oy.
\(\Rightarrow\widehat{yOz}=\widehat{xOy}-\widehat{xOz}=135^o-45^o=90^o\left(đpcm\right)\)