Trong 1 phút tổ 1, 2, 3 làm được số công việc sân trường là:

\(1\div12=\dfrac{1}{12}\)  ( sân trường ) 

Trong 1 phút tổ 2, 3, 4 làm được số công việc sân trường là:

\(1\div15=\dfrac{1}{15}\)  ( sân trường )

Trong 1 phút, tổ 1,4 làm được số công việc sân trường là:

\(1\div20=\dfrac{1}{20}\)  ( sân trường )

Trong 1 phút, cả 3 lần tổ 1,2,3; 2,3,4;1,4 làm được số công việc sân trường là:

\(\dfrac{1}{12}+\dfrac{1}{15}+\dfrac{1}{20}=\dfrac{1}{5}\)  ( sân trường )

Trong 1 phút, cả 4 tổ làm được là:

\(\dfrac{1}{5}\div2=\dfrac{1}{10}\)  ( sân trường )

Cả 4 tổ làm công việc sân trường hết số phút là:

\(1\div\dfrac{1}{10}=10\)  ( phút )

Đáp số: \(10\) phút

a, $5^{3} =5\times5\times5=125$

$3^{5} =3\times3\times3=27$

$125>27=>5^{3}>3^{5}$

$3^{2}=3\times3=9$

$2^{3}=2\times2\times2=8$

$9>8=>3^{2}>2^{3}$

$2^{6} =2\times2\times2\times2\times2\times2=64$

$6^{2}=6\times6=36$

$64>36=>2^{6}>6^{2}$

b, $2015\times2017=2015\times(2016+1)=2015\times2016+2015$

$2016^{2}=2016\times2016=2016\times(2015+1)=2016\times2015+2016$

$2015\times2016+2015<2016\times2015+2016=>2015\times2017<2016^{2}$

c, $199^{20}=199^{4\times5}=(199^{4})^{5}= 1568239201^{5}$

$2003^{15}=2003^{3\times5}=(2003^{3})^5 =8036054027^{5}$

$1568239201<8036054027=>199^{20}<2003^{15}$

d, $3^99 =3^{3\times33}=(3^{3})^{33}=27^{33}>27^{21}$

$11^{21}<27^{21}=>3^{99}>11^{21}$

$3^{2n}=9^n$

$2^{3n}=8^n$

$9>8=>3^{2n}>2^{3n}$

So sánh các số sau

a) 5³ và 3⁵

5³ = 125

3⁵ = 243

=> 5³ < 3⁵

3² và 2³

3² = 9

2³ = 8

=> 3² > 2³

2⁶ và 6²

2⁶ = 64

6² = 36

=> 2⁶ > 6²

b) 2015 x 2017 và 2016²

2015 x 2017 

= 2015 x ( 2016 + 1 ) 

= 2015 x 2016 + 2015 

2016²

= 2016 x 2016

= 2016 x ( 2015 + 1 )

= 2016 x 2015 + 2016

Vì: 2015 < 2016

=> 2015 x 2017 < 2016²

c) 199²⁰ và 2003¹⁵

199²⁰ < 200²⁰ = ( 2³ x 5² )²⁰ = 2⁶⁰ x 5⁴⁰

2003¹⁵ > 2000¹⁵ = ( 2 x 10³ )¹⁵ = ( 2⁴ x 5³ )¹⁵ = 2⁶⁰ x 5⁴⁵

=> 2003¹⁵ > 199²⁰

d) 3⁹⁹ và 11²¹

3⁹⁹ = ( 3³ )³³ = 27³³ > 27²¹

Vì: 27 > 11

=> 27²¹ > 11²¹ 

=> 3⁹⁹ > 11²¹

3²ⁿ và 2³ⁿ

3²ⁿ = ( 3² )ⁿ = 9ⁿ

2³ⁿ = ( 2³ )ⁿ = 8ⁿ

Vì 9 > 8

=> 9ⁿ > 8ⁿ

=> 3²ⁿ > 2³ⁿ

Vậy 3²ⁿ > 2³ⁿ

Diện tích con đường là :

\(5.50:2=125\left(m^2\right)\)

Diện tích mảnh đất hình tam giác đó là:

\(50.70:2=1750\left(m^2\right)\)

Diện tích mảnh đất còn lại là:

\(1750-125=1625\left(m^2\right)\)

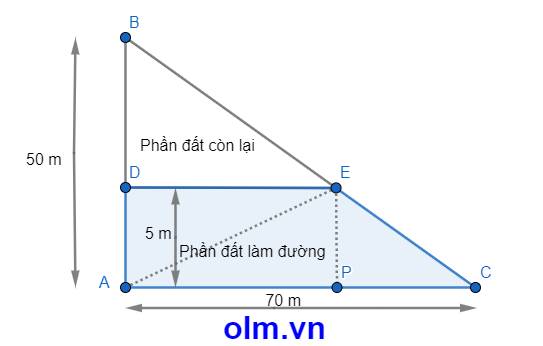
Gọi tên mảnh đất hình tam giác là mảnh đất tam giác ABC có các kích thước thỏa nãn đề bài như hình vẽ trên.

Chiều cao của \(\Delta\)AEC chính là chiều rộng của đường và bằng 5 m

S_AEC = 70 \(\times\) 5 : 2 = 175 (m²)

Diện tích mảnh đất tam giác ABC là : 70 \(\times\) 50 : 2 = 1750 (m²)

S_ABE = S_ABC - S_AEC 

Diện tích tam giác ABE là: 1750 - 175 = 1575 (m²)
Chiều cao \(\Delta\)ABE là DE cũng là chiều cao của \(\Delta\)BDE và bằng:

1575  \(\times\) 2 : 50 = 63 (m)

Độ dài đáy BD là: 50 - 5 = 45 (m)

Diện tich còn lại của mảnh đất sau khi làm đường là diện tích tam giác BDE và bằng:

45 \(\times\) 63 : 2 = 1417,5 (m²)

Đáp số: 1417,5 m²

a) Ta có:

-Các thừa số có tận cùng bằng 0 là: (10;20;30;40;50;60;70;80;90;100) và tận cùng bằng 5 là: (15;25;35;45;55;65;75;85;95)

-Tích của 10 x 20 x 30 x 40 x ... x 100 có tận cùng 10 chữ số 0

- Tích của 50 và một số chẵn (ví dụ: 50 x 2=100 ) tận cùng bằng 2 chữ số 0.

- Tích 25 x 4 cũng bằng tận cùng bằng 2 chữ số 0.

-Những số có tận cùng với 5 như 15,25,35,...,95 nhân với một số chẵn đều có tận cùng bằng 1 chữ số 0

Ngoài ra không có 2 thừa số nào cho tích cũng bằng 0

Ta có: 10+2+2+2+1+1+1+1+1+1+1+1=24 chữ số 0

Vậy 1 x 2 x 3 x . . . x 99 x 100 có tận cùng 24 chữ số 0

b) Có tận cùng bằng 2 chữ số 0

c)Có tận cùng bằng 4 chữ số 0

\(B=\dfrac{1}{2}-\left(\dfrac{1}{2}\right)^2+\left(\dfrac{1}{2}\right)^3-\left(\dfrac{1}{2}\right)^4+...-\dfrac{1}{2022}+\dfrac{1}{2023}\\ \Rightarrow B=\dfrac{2}{2^2}-\dfrac{1}{2^2}+\dfrac{2}{2^4}-\dfrac{1}{2^4}+...+\dfrac{2}{2^{2024}}-\dfrac{1}{2^{2024}}\)

\(\Rightarrow B=\dfrac{1}{2^2}+\dfrac{1}{2^4}+\dfrac{1}{2^6}+...+\dfrac{1}{2^{2024}}\)

\(\Rightarrow B=\dfrac{2^{2022}}{2^{2024}}+\dfrac{2^{2020}}{2^{2024}}+...+\dfrac{1}{2^{2024}}\\ \Rightarrow2^2B=\dfrac{2^{2024}}{2^{2024}}+\dfrac{2^{2022}}{2^{2024}}+...+\dfrac{2^2}{2^{2024}}\)

\(\Rightarrow4B-B=\dfrac{2}{2^{2024}}-\dfrac{1}{2^{2024}}\\ \Rightarrow3B=1-\left(\dfrac{2}{2^{2024}}+\dfrac{1}{2^{2024}}\right)\)

\(\Rightarrow3B=1-\dfrac{3}{2^{2024}}\\ \Rightarrow B=\dfrac{1-\dfrac{3}{2^{2024}}}{3}\)

\(\Rightarrow B=\dfrac{3\left(\dfrac{1}{3}-\dfrac{1}{2^{2024}}\right)}{3}\\ B=\dfrac{1}{3}-\dfrac{1}{2^{2024}}\)

\(S=1+2+...+2^{2017}\)

\(2S=2+2^2+...+2^{2018}\)

\(2S-S=2+2^2+...+2^{2018}-1-2-...-2^{2017}\)

\(S=2^{2018}-1\)

\(S=3+3^2+...+3^{2017}\)

\(3S=3^2+3^3+...+3^{2018}\)

\(3S-S=3^2+3^3+...+3^{2018}-3-3^2-...-3^{2017}\)

\(2S=3^{2018}-3\)

\(S=\dfrac{3^{2018}-3}{2}\)

\(S=4+4^2+...+4^{2017}\)

\(4S=4^2+4^3+...+4^{2018}\)

\(4S-S=4^2+4^3+...+4^{2018}-4-4^2-...-4^{2017}\)

\(3S=4^{2018}-4\)

\(S=\dfrac{4^{2018}-4}{3}\)

\(S=5+5^2+...+5^{2017}\)

\(5S=5^2+5^3+...+5^{2018}\)

\(5S-S=5^2+5^3+...+5^{2018}-5-5^2-...-5^{2017}\)

\(4S=5^{2018}-5\)

\(S=\dfrac{5^{2018}-5}{4}\)

a) S=1+2+2²+...+2²⁰¹⁷

=> 2S=2.(1+2+2²+...+2²⁰¹⁷)

=>2S=2+2²+2³+...+2²⁰¹⁸

=>S=(2+22+23+ ..+22018) - (1+2+22+ ....+22017 )

=> S =22018-1

`@` `\text {Ans}`

`\downarrow`

May mỗi cái áo hết số mét vải là:

                `17 \div 10  = 1,7` (m)

May 9 cái áo như thế hết số mét vải là:

                `1,7 \times 9 = 15,3` (m)

                                  Đáp số: `15,3`m.

\(\left(3x-4\right)^7=128\)

\(\left(3x-4\right)^7=2^7\)

\(3x-4=2\)

\(3x=2+4\)

\(3x=6\)

\(x=2\)

(3x-4)⁷=128=2⁷

=>3x-4=2

=>3x=2+4=6

=>x=6:3=2

$C=1+4+...+4^{6}$

$4C=4+4^{2}+...+4^{7}$

$4C-C=4+4^{2}+...+4^{7}-1-4-...-4^{6}$

$3C=4^{7}-1$

$C=\dfrac{4^{7}-1}{3}$

Để tính tổng S = 1 + 4 + 4^2 + ... + 4^6, ta có thể sử dụng công thức tổng của cấp số nhân:

S = (a * (r^n - 1)) / (r - 1)

Trong đó:
- a là số hạng đầu tiên của dãy (a = 1)
- r là công bội của dãy (r = 4)
- n là số lượng số hạng trong dãy (n = 6)

Áp dụng vào bài toán, ta có:

S = (1 * (4^6 - 1)) / (4 - 1)
= (4^6 - 1) / 3

Để chứng minh A = {(4^7 - 1) : 3}, ta cần chứng minh rằng S = (4^7 - 1) : 3.

Ta có:
(4^7 - 1) : 3 = (4^7 - 1) / 3

Để chứng minh hai biểu thức trên bằng nhau, ta sẽ chứng minh rằng (4^7 - 1) / 3 = (4^6 - 1) / 3.

Ta có:
(4^7 - 1) / 3 = (4^6 * 4 - 1) / 3
= (4^6 * 4 - 1 * 4^0) / 3
= (4^6 * 4 - 4^6) / 3
= 4^6 * (4 - 1) / 3
= (4^6 - 1) / 3

Vậy ta đã chứng minh được A = {(4^7 - 1) : 3}.

Bạn Linh có số quyển sách là: 

68 x 2 = 136 ( quyển sách )

Bạn Na có số quyển sách là:

136 x 3 = 408 ( quyển sách )

Đáp số: Bạn Linh có 136 quyển sách

Bạn Na có 408 quyển sách

Cho mình bổ sung nếu hỏi cả 2 bạn có bao nhiêu quyển sách thì:

136 + 408 = 544 ( quyển sách )

Đáp số: 544 quyển sách