Tổng của 2 số sau khi gấp 3 lần số thứ hai lên hơn tổng hai số ban đầu là:
    \(89668-68080=21588\) (đơn vị)
Giá trị số thứ hai là:
    \(21588:2=10794\)
Giá trị số thứ nhất là:
    \(68080-10794=57286\)
       Đáp số: ....

Gọi a là sô thứ 1

Gọi b là sô thứ 2

Theo đề bài ta có :

Tồng 2 số lúc đầu : \(a+b=68080\left(1\right)\)

Tổng 2 số lúc sau : \(a+3xb=89668\left(2\right)\)

\(\left(1\right)-\left(2\right)\Rightarrow2xb=\text{21588}\Rightarrow b=\text{21588}:2=\text{10794}\)

\(\Rightarrow a=68080-\text{10794}=\text{57286}\)

Vây số thứ 1 là 57286

       số thứ 1 là 10794

\(A=\dfrac{x^2}{x-2}=\dfrac{x^2-4+4}{x-2}=\dfrac{\left(x-2\right)\left(x+2\right)+4}{x-2}\)

\(=x+2+\dfrac{4}{x-2}=x-2+\dfrac{4}{x-2}+4\)

mà \(x-2+\dfrac{4}{x-2}\ge2.\sqrt[]{x-2.\dfrac{4}{x-2}}=2.2=4\) Bất đẳng thức Cauchy)

\(\Rightarrow A=x-2+\dfrac{4}{x-2}+4\ge8\)

\(\Rightarrow GTNN\left(A\right)=8\)

Bài giải

$250km$ gấp số lần $100km$ là:

$250:100=2,5$(lần)

Đi quãng đường dài $250km$ thì ô tô đó tiêu thụ:

$12\times2,5=30(l)$

Đ/s: $30l$ xăng

Số lít xăng 250 km tiêu thụ là :

\(250x12:100=30\left(l\right)\)

0,25:5=0,05

$0,25:5=25:100:5=25:5:100=5:100=0,05$

Bài giải

Lớp $4A$ trồng được là:

$(568+36):2=302$(cây)

Lớ $4B$ trồng được là:

$568-302=266$(cây)

Đ/s: Lớp $4A$: $302$ cây; Lớp $4B$: $266$ cây

Số cây lớp 4A trồng được là: (568 + 36) : 2 = 302 ( cây)

Số cây lớp 4B trồng được là: 302 – 36 = 266 (cây)

Đáp số: Lớp 4A: 302 cây. Lớp 4B: 266 cây

\(A=\dfrac{1999^{1999}+1}{1999^{1998}+1}\)

\(\dfrac{1}{1999}A=\dfrac{1999^{1999}+1}{1999^{1999}+1999}\)

\(\dfrac{1}{1999}A=\dfrac{1999^{1999}}{1999^{1999}}-\dfrac{1998}{1999^{1999}+1999}\)

\(\dfrac{1}{1999}A=1-\dfrac{1998}{1999^{1999}+1999}\)

\(B=\dfrac{1999^{2000}+1}{1999^{1999}+1}\)

\(\dfrac{1}{1999}B=\dfrac{1999^{2000}+1}{1999^{2000}+1999}\)

\(\dfrac{1}{1999}B=\dfrac{1999^{2000}}{1999^{2000}}-\dfrac{1998}{1999^{2000}+1999}\)

\(\dfrac{1}{1999}B=1-\dfrac{1998}{1999^{2000}+1999}\)

Vì  \(\dfrac{1998}{1999^{1999}+1999}>\dfrac{1998}{1999^{2000}+1999}=>\dfrac{1}{1999}A< \dfrac{1}{1999}B=>A< B\)

\(A=\dfrac{1999^{1999}+1}{1999^{1998}+1}=\dfrac{\left(1999^{1999}+1\right)^2}{\left(1999^{1998}+1\right)\left(1999^{1999}+1\right)}\)

\(A=\dfrac{\left(1999^{1999}\right)^2+2.1999^{1999}+1}{\left(1999^{1998}+1\right)\left(1999^{1999}+1\right)}\left(1\right)\)

\(B=\dfrac{1999^{2000}+1}{1999^{1999}+1}=\dfrac{\left(1999^{2000}+1\right)\left(1999^{1998}+1\right)}{\left(1999^{1998}+1\right)\left(1999^{1999}+1\right)}\)

\(B=\dfrac{\left(1999.1999^{1999}+1\right)\left(\dfrac{1}{1999}.1999^{1999}+1\right)}{\left(1999^{1998}+1\right)\left(1999^{1999}+1\right)}\)

\(B=\dfrac{\left(1999^{1999}\right)^2+1999.1999^{1999}+\dfrac{1}{1999}.1999^{1999}+1}{\left(1999^{1998}+1\right)\left(1999^{1999}+1\right)}\)

\(B=\dfrac{\left(1999^{1999}\right)^2+\left(1999+\dfrac{1}{1999}\right).1999^{1999}+1}{\left(1999^{1998}+1\right)\left(1999^{1999}+1\right)}\left(2\right)\)

mà \(\left(1999+\dfrac{1}{1999}\right)>2\)

\(\left(1\right).\left(2\right)\Rightarrow A< B\)

Nửa chu vi mảnh vườn đó là:

284 : 2 = 142 ( m )

Chiều dài mảnh vườn đó là:

( 142 + 14 ) : 2 = 78 ( m )

Chiều rộng mảnh vườn đó là:

142 - 78 = 64 ( m )

Diện tích mảnh vườn đó là:

78 x 64 = 4992 ( m² )

Diện tích để trồng rau là:
  4992 : 4 = 1248 ( m² )

Số yến rau thu hoạch được trên thửa ruộng đó là:

1248 : 8 x 10 = 1560 ( kg )

                    = 156 yến

Đáp số:............

Chúc bạn học tốt!

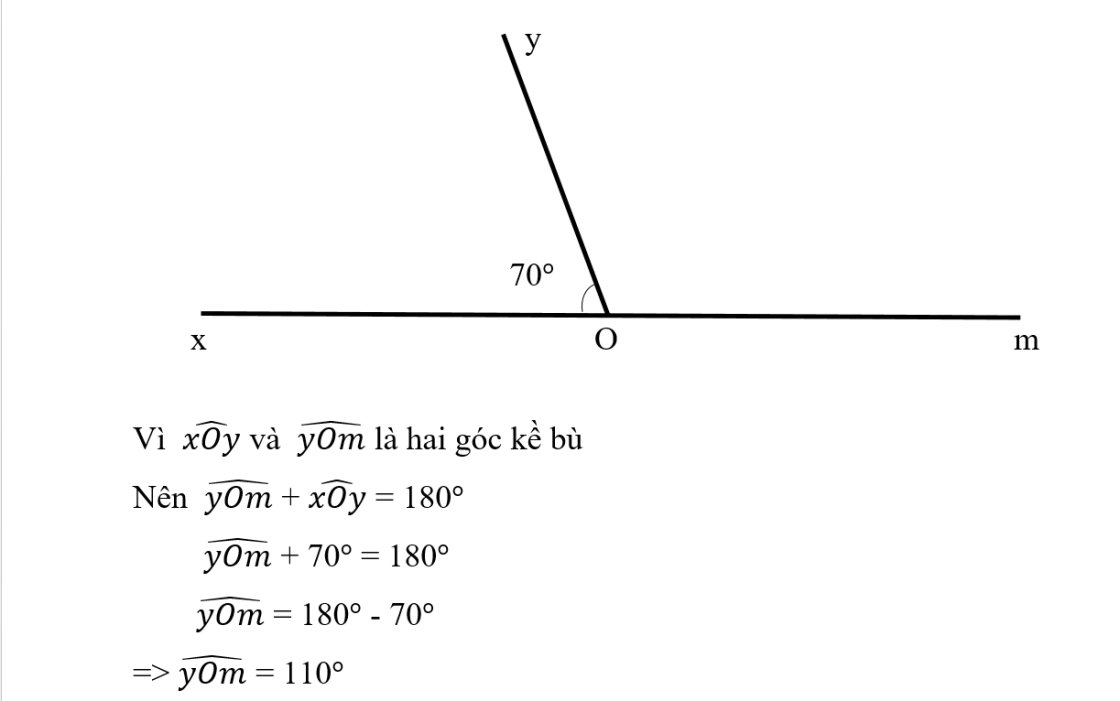
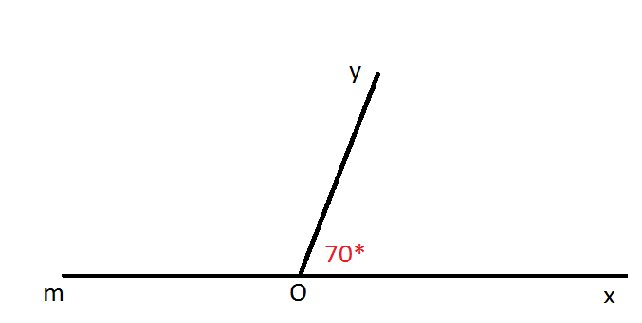Ta có: yOm + xOy = 180* ( 2 góc kề bù)
    T/s yOm + 70* = 180* ⇒ yOm = 110*

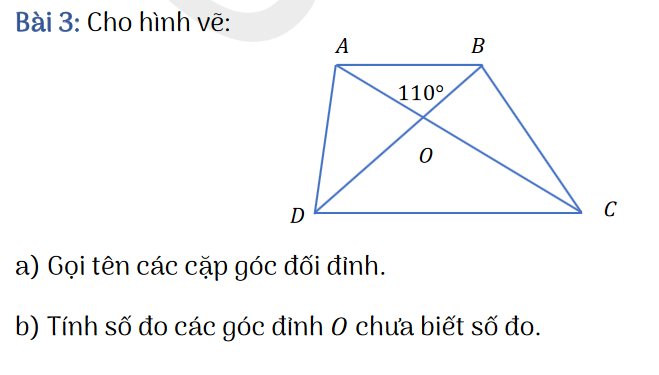
a, Các cặp góc đối đỉnh là: \(\widehat{AOB}\) và \(\widehat{COD}\), \(\widehat{AOD}\) và \(\widehat{BOC}\)

b, \(\widehat{COD}=\widehat{AOB}=110^o\)

\(\widehat{AOD}=\widehat{BOC}=180^o-110^o=70^o\)