Tổng số điểm trên đoạn thẳng AB là 2023+2=2025(điểm)

Số cách lấy 2 điểm trong 2025 điểm là \(C^2_{2025}\left(cách\right)\)

=>Số tam giác tạo thành là \(C^2_{2025}\)(tam giác)

C nằm giữa A và B

=>CA+CB=AB

=>CB+2=7

=>CB=5(cm)

D là trung điểm của AC

=>\(AD=DC=\dfrac{AC}{2}=\dfrac{2}{2}=1\left(cm\right)\)

E là trung điểm của CB

=>\(EC=EB=\dfrac{BC}{2}=2,5\left(cm\right)\)

CA và CB là hai tia đối nhau

=>CD và CE là hai tia đối nhau

=>C nằm giữa D và E

=>DE=DC+CE=2,5+1=3,5(cm)

F là trung điểm của DE

=>\(DF=\dfrac{DE}{2}=1,75\left(cm\right)\)

Vì DC<DF

nên C nằm giữa D và F

=>DC+CF=DF

=>CF+1=1,75

=>CF=0,75(cm)

Lời giải:
\(B=(\frac{1}{101}+\frac{1}{102}+...+\frac{1}{120})+(\frac{1}{121}+...+\frac{1}{140})+(\frac{1}{141}+....+\frac{1}{160})+(\frac{1}{161}+...+\frac{1}{180})+(\frac{1}{181}+...+\frac{1}{200})\)

\(> \frac{20}{120}+\frac{20}{140}+\frac{20}{160}+\frac{20}{180}+\frac{20}{200}=\frac{1627}{2520}> \frac{5}{8}\)

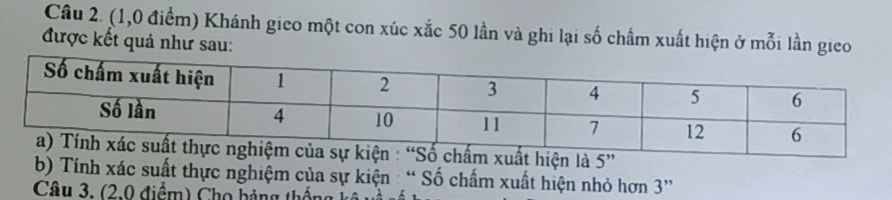
a: Gọi A là biến cố "Số chấm xuất hiện là 5"

=>n(A)=12

=>Xác suất thực nghiệm là \(P_A=\dfrac{12}{50}=0,24\)

b: Gọi B là biến cố "Số chấm xuất hiện nhỏ hơn 3"

=>n(B)=4+10=14

=>Xác suất thực nghiệm là \(P_B=\dfrac{14}{50}=0,28\)

D góc bẹt

\(D\)

a: B nằm giữa A và C

=>AB+BC=AC

=>BC+3=7

=>BC=4(cm)

b: M là trung điểm của AB

=>\(AM=BM=\dfrac{AB}{2}=1,5\left(cm\right)\)

Vì M nằm giữa A và B

và B nằm giữa A và C

nên M nằm giữa A và C

=>AM+MC=AC

=>MC+1,5=7

=>MC=5,5(cm)

a.Vì B nằm giữa A,C

→BC=AC−AB=4(cm)

b.Vì M là trung điểm AB→MA=MB=12AB=1.5 và M nằm giữa A,B

Mà B nằm giữa A,C

→B nằm giữa M,C

→MC=MB+BC=5.5(cm)

a) A = {xanh, đỏ, vàng, tím}

b) Trường hợp xấu nhất có thể xảy ra là lấy được 6 bi tím, 7 bi vàng, 7 bi đỏ và 7 bi xanh

Cần lấy thêm 1 viên bi nữa sẽ chắc chắn có ít nhất 8 viên bi cùng màu

Số viên bi cần lấy:

6 + 7 + 7 + 7 + 1 = 28 (viên)

a) A = {xanh, đỏ, vàng, tím}

b) Trường hợp xấu nhất có thể xảy ra là lấy được 6 bi tím, 7 bi vàng, 7 bi đỏ và 7 bi xanh

Cần lấy thêm 1 viên bi nữa sẽ chắc chắn có ít nhất 8 viên bi cùng màu

Số viên bi cần lấy:

6 + 7 + 7 + 7 + 1 = 28 (viên)

Lời giải:

Coi quãng đường $AB$ dài $x$ km. Sau khi chạy được 2/5 quãng đường đầu thì còn $x-\frac{2}{5}x=\frac{3}{5}x$ (km) 

Vậy kể từ giờ thứ hai ô tô còn $\frac{3}{5}x$ km đường. Giờ thứ hai sau khi xe chạy được 2/5 quãng đường thì đi còn 3/5 quãng đường. 3/5 quãng đường này dài: $40+4=44$ (km) 

Độ dài quãng đường ô tô đi kể từ giờ thứ hai (tức là $\frac{3}{5}x$) dài:

$44:\frac{3}{5}=73,3$ (km)

Độ dài quãng đường AB là:

$x=73,3:\frac{3}{5}=122$ (km)

Vận tốc trung bình: $122:3=40,7$ (km/h)

\(\dfrac{1}{2^2}< \dfrac{1}{1\cdot2}=1-\dfrac{1}{2}\)

\(\dfrac{1}{3^2}< \dfrac{1}{2\cdot3}=\dfrac{1}{2}-\dfrac{1}{3}\)

...

\(\dfrac{1}{55^2}< \dfrac{1}{54\cdot55}=\dfrac{1}{54}-\dfrac{1}{55}\)

Do đó: \(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{55^2}< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{54}-\dfrac{1}{55}\)

=>\(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{55^2}< 1\)

=>\(\dfrac{4}{2^2}+\dfrac{4}{3^2}+...+\dfrac{4}{55^2}< 4\)

Lời giải:
\(S=\frac{1}{3}-\frac{2}{3^2}+\frac{3}{3^3}-\frac{4}{3^4}+....+\frac{99}{3^{99}}-\frac{100}{3^{100}}\\ 3S=1-\frac{2}{3}+\frac{3}{3^2}-\frac{4}{3^3}+....+\frac{99}{3^{98}}-\frac{100}{3^{99}}\\ \Rightarrow S+3S=1-\frac{1}{3}+\frac{1}{3^2}-\frac{1}{3^3}+...-\frac{1}{3^{99}}-\frac{100}{3^{100}}\)

\(\Rightarrow 4S+\frac{100}{3^{100}}=1-\frac{1}{3}+\frac{1}{3^2}-\frac{1}{3^3}+...-\frac{1}{3^{99}}\)

\(3(4S+\frac{100}{3^{100}})=3-1+\frac{1}{3}-\frac{1}{3^2}+....-\frac{1}{3^{98}}\)

\(\Rightarrow 4(4S+\frac{100}{3^{100}})=3-\frac{1}{3^{99}}\)

\(S=\frac{3}{16}-\frac{1}{16.3^{99}}-\frac{100}{3^{100}}< \frac{3}{16}< \frac{1}{5}\)