một số tự nhiên chia cho 45 dư 20 hỏi số đó có chia hết cho 5 và 15 không
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=\dfrac{6n-1}{3n-2}\)
\(\Rightarrow A=\dfrac{6n-4+3}{3n-2}\)
\(\Rightarrow A=\dfrac{2\left(3n-2\right)+3}{3n-2}\)
\(\Rightarrow A=2+\dfrac{3}{3n-2}\ge2+\dfrac{3}{3.1-2}=5\left(n=1\in Z\right)\)
\(\Rightarrow Min\left(A\right)=5\left(n=1\right)\)

Bài 61:
a, 5,5 : \(\dfrac{1}{2}\) = \(\dfrac{55}{10}\) : \(\dfrac{1}{2}\) = \(\dfrac{11}{1}\)
Vậy 5,5 : \(\dfrac{1}{2}\) = \(\dfrac{11}{1}\)
b, 1\(\dfrac{5}{7}\): (-1\(\dfrac{3}{9}\)) = \(\dfrac{12}{7}\): (-\(\dfrac{4}{3}\)) = - \(\dfrac{9}{7}\) = \(\dfrac{-9}{7}\)
vậy 1\(\dfrac{5}{7}\) = \(\dfrac{-9}{7}\)
c, (-0,12) : 2\(\dfrac{3}{4}\) = - \(\dfrac{12}{100}\) : \(\dfrac{11}{4}\) = - \(\dfrac{12}{275}\) = \(\dfrac{-12}{275}\)
vậy (-0,12) : 2\(\dfrac{3}{4}\) = \(\dfrac{-12}{275}\)
d, (-2,5) : 3,5 = \(\dfrac{-25}{10}\) : \(\dfrac{35}{10}\) = \(\dfrac{-5}{7}\)
vậy -2,5 : 3,5 = \(\dfrac{-5}{7}\)
Bài 62: (-5) : 10 = - \(\dfrac{1}{2}\); \(\dfrac{2}{5}\) : \(\dfrac{9}{7}\) = \(\dfrac{14}{45}\);
(-3,11) : 12,5 = - \(\dfrac{311}{1250}\); - \(\dfrac{14}{5}\) : 9 = - \(\dfrac{14}{45}\)
(-1,5): 3 = \(-\dfrac{1}{2}\); - \(\dfrac{311}{50}\): 25 = - \(\dfrac{311}{1250}\)
\(\dfrac{-5}{10}\) = \(\dfrac{-1,5}{3}\); \(\dfrac{-3,11}{12,5}\) = \(\dfrac{\dfrac{-311}{50}}{25}\)

- Với \(0< x;y< 1\)
\(x^2>x^{2003}\left(1\right)\)
\(y^2>y^{2003}\left(2\right)\)
\(z^2>z^{2003}\left(3\right)\)
\(\left(1\right)+\left(2\right)+\left(3\right)\Rightarrow M=x^2+y^2+z^2>x^{2003}+y^{2003}+z^{2003}=3\)
\(\Rightarrow\) Không có giá trị max của M.
- Với \(x;y\ge1\)
\(x^2\le x^{2003}\left(1\right)\)
\(y^2\le y^{2003}\left(2\right)\)
\(z^2\le z^{2003}\left(3\right)\)
\(\left(1\right)+\left(2\right)+\left(3\right)\Rightarrow x^2+y^2+z^2\le x^{2003}+y^{2003}+z^{2003}=3\)
\(\Rightarrow Max\left(M\right)=3\left(x=y=z=1\right)\)

\(xy^2+2xy-8y+x=0\)
\(\Leftrightarrow xy^2+2xy+x=8y\)
\(\Leftrightarrow x\left(y^2+2y+1\right)=8y\)
\(\Leftrightarrow x\left(y+1\right)^2=8y\)
\(\Leftrightarrow\left(y+1\right)^2=\dfrac{8y}{x}=2^2.\dfrac{2y}{x}\left(x\ne0\right)\left(1\right)\)
Ta thấy \(VP=\left(y+1\right)^2\) là số chính phương lẻ hoặc chẵn
mà \(VP=2^2.\dfrac{2y}{x}\) là số chính phương chẵn \(\left(2^2;\dfrac{2y}{x}⋮2\right)\) và \(\dfrac{2y}{x}\) cũng là số chính phương
\(\Rightarrow\left(y+1\right)^2\) là số chính phương chẵn
\(\Rightarrow y\) là số lẻ
Vậy để thỏa \(\left(1\right)\) ta thấy \(y=1;x=2\)
\(\Rightarrow\left(x;y\right)\in\left\{\left(2;1\right)\right\}\left(x;y\in Z\right)\)
- Nhân cả hai vế của phương trình với y, ta được:
xy^3 + 2xy^2 - 8y^2 + x = 0
- Đặt z=xy, ta được:
z^3 + 2z^2 - 8z + x = 0
- Phương trình này có thể được giải bằng cách sử dụng phương pháp phân tích đa thức. Ta có:
z = (1 + 2 \sqrt{2}) \pm (1 - 2 \sqrt{2}) \sqrt{3}
- Thay z bằng xy, ta được:
xy = (1 + 2 \sqrt{2}) \pm (1 - 2 \sqrt{2}) \sqrt{3}
- Giải nghiệm nguyên cho x và y, ta được:
(x, y) = (1, 1), (1, -1), (-1, 1), (-1, -1)
Vậy, nghiệm nguyên của phương trình xy2+2xy−8y+x=0 là (1,1),(1,−1),(−1,1),(−1,−1).
thumb_upthumb_down
share
Tìm trên Google

\(32:\left(-\dfrac{16}{3}\right)=32\times\left(-\dfrac{3}{16}\right)=\dfrac{16\times2\times\left(-3\right)}{16}=-6\)
32 : ( - \(\dfrac{16}{3}\)) = 32 x ( - \(\dfrac{3}{16}\)) = - 6


Ta có: \(\dfrac{82}{67}< \dfrac{88}{67}\) mà \(\dfrac{88}{65}>\dfrac{88}{67}\)
Vậy \(\dfrac{82}{67}< \dfrac{88}{65}\)

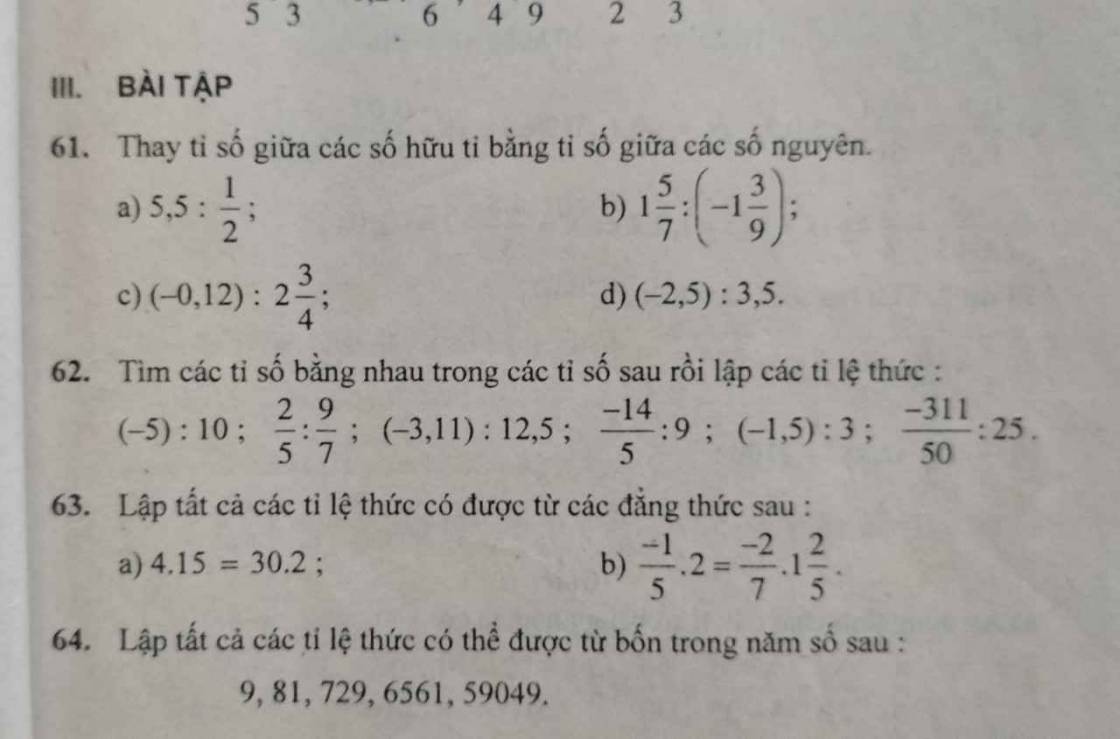
Đặt \(a=45k+20\left(k\in N\right)\)
\(a=45k+20=5\left(9k+4\right)⋮5\)
\(a=45k+20\); \(45k⋮15\) nhưng \(20\) không chia hết cho \(15\)
Vậy \(45\) dư \(20\) chia hết cho \(5\) nhưng không chia hết cho \(15\)
Ta đặt số tự nhiên có dạng 45k+20 (k\(\inℕ\))
Ta có
+, 45k+20\(⋮5\), do 45 chia hết cho 5, 20 cũng chia hết cho 5
=>45k+20 chia hết cho 5
+,45k+20\(⋮̸5\), do 20 không chia hết cho 15
=>45k+20 không chia hết cho 15
Vậy 45k+20 chia hết cho 5.