Không quy đồng, hãy so sánh 2 phân số: 2005/2001 và 2048/2028
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{x}{0,2}=\dfrac{y}{0,75}=\dfrac{z}{0,125}\)
\(\Rightarrow\dfrac{x^2}{\left(0,2\right)^2}=\dfrac{y^2}{\left(0,75\right)^2}=\dfrac{z^2}{\left(0,125\right)^2}=\dfrac{x^2+y^2+z^2}{\left(0,2\right)^2+\left(0,75\right)^2+\left(0,125\right)^2}=\dfrac{3956}{2^2.10^{-4}+75^2.10^{-4}+125^2.10^{-4}}=\dfrac{3956}{10^{-4}.\left(4+5625+15625\right)}=\dfrac{3956.10^4}{21254}\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{3956.10^4}{21254}.0,2=\dfrac{7912.10^3}{21254}\\y=\dfrac{3956.10^4}{21254}.0,75=\dfrac{29670.10^3}{21254}\\z=\dfrac{3956.10^4}{21254}.0,125=\dfrac{4945.10^3}{21254}\end{matrix}\right.\)
Vậy \(M=x+y+z=\dfrac{7912.10^3+29670.10^3+4945.10^3}{21254}\)
\(M=\dfrac{\left(7912+29670+4945\right).10^3}{21254}=\dfrac{42527.10^3}{21254}\)

1)
a) 18 = 2.3²
30 = 2.3.5
ƯCLN(18; 30) = 2.3 = 6
b) 24 = 2³.3
48 = 2⁴.3
ƯCLN(24; 48) = 2³.3 = 24
c) 18 = 2.3²
30 = 2.3.5
15 = 3.5
ƯCLN(18; 30; 15) = 3
d) 24 = 2³.3
48 = 2⁴.3
36 = 2².3²
ƯCLN(24; 48; 36) = 2².3 = 12
2) a) 174 = 18 . 9 + 12
18 = 12 . 1 + 6
12 = 6 . 2
Vậy ƯCLN(174; 18) = 6
b) 124 = 16 . 7 + 12
16 = 12 . 1 + 4
12 = 4 . 3
⇒ ƯCLN(124; 16) = 4
⇒ BCNN(124; 16) = 124 . 16 : 4 = 496

Bài 13
a) A = 1 + 2 + 3 + ... + 10
Số số hạng: 10 - 1 + 1 = 10
A = (10 + 1) . 10 : 2 = 55
b) B = 2 + 4 + 6 + ... + 20
Số số hạng: (20 - 2) : 2 + 1 = 10
B = (20 + 2) . 10 : 2 = 110
c) C = 9 + 11 + 13 + ... + 29
Số số hạng: (29 - 9) : 2 + 1 = 11
C = (29 + 9) . 11 : 2 = 209
d) D = 5 + 10 + 15 + 20 + ... + 100
Số số hạng: (100 - 5) : 5 + 1 = 20
D = (100 + 5) . 20 : 2 = 1050

Gọi a, b, c lần lượt là số tuổi của ông nội, cha và con (a, b, c ∈ Z⁺)
Do số tuổi của ông nội, cha và con tỉ lệ với 21; 14; 5 nên:
a/21 = b/14 = c/5
Do tổng số tuổi là 120 nên:
a + b + c = 120
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
a/21 = b/14 = c/5 = (a + b + c)/(21 + 14 + 5) = 120/40 = 3
*) a/21 = 3 ⇒ a = 3 . 21 = 63 (nhận)
*) b/14 = 3 ⇒ b = 3 . 14 = 42 (nhận)
*) c/5 = 3 ⇒ c = 3 . 5 = 15 (nhận)
Vậy ông nội 63 tuổi, cha 42 tuổi, con 15 tuổi
Gọi số tuổi của ông nội ,cha ,con tỉ lệ với 21;14;5 lần lượt là: x;y;z
=>\(\dfrac{x}{21}\)=\(\dfrac{y}{14}\)=\(\dfrac{z}{5}\) và x+y+z=120 Áp dụng tính chất dãy tỉ số bằng nhau
=>\(\dfrac{x}{21}\)=\(\dfrac{y}{14}\)=\(\dfrac{z}{5}\)=\(\dfrac{x+y+z}{21+14+5}\)=\(\dfrac{120}{40}\)=3
=>Số tuổi của ông nội là:3x21=63(tuổi)
Số tuổi của bố là:3x14=42(tuổi)
Số tuổi của con là:3x5=15(tuổi)

62 . 10 : { 780 : [ 103 - ( 2 . 53 + 35 . 14 ) ] }
= 360 : { 780 : [ 1000 - ( 250 + 490 ) ] }
= 360 : { 780 : [ 1000 - 740 ] }
= 360 : { 780 : 260 }
= 360 : 3
= 120.

Trường hợp xấu nhất bốc phải:
8 bi vàng + 8 bi xanh + 8 bi tím = 24 (viên bi)
Để chắc chắc lấy được 9 viên bi cùng màu thì Hampard cần bốc ít nhất số bi là:
24 + 1 = 25 ( viên bi)
Kết luận: Để chắc chắn lấy được 9 viên bi cùng màu thì Hampard cần bốc ít nhất 25 viên bi


C = 1 + 31 + 32 + 33 + ...+ 399
3C = 31 + 32 + 33+...+ 399 + 3100
3C - C = 3100 - 1
2C = 3100 - 1
C = \(\dfrac{3^{100}-1}{^{ }2}\)
C=1+3+32+...+399
=>3C=3+32+...+3100
=>3C-C=2C=(3+32+...+3100)-(1+3+32+...+399)=3100-1
=>C=\(\dfrac{3^{100}-1}{2}\)

a,18=2x32
b,48=24x3
c,2x9x2012=23x32x503
c,20012012=32012x232012x292012.
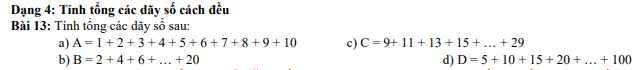
\(\dfrac{2005}{2001}< 1;\dfrac{2048}{2028}>1\Rightarrow\dfrac{2005}{2001}< \dfrac{2048}{2028}\)
\(\dfrac{2005}{2001}\) = 1 + \(\dfrac{4}{2001}\) = 1 + \(\dfrac{20}{10005}\)
\(\dfrac{2048}{2028}\) = 1+ \(\dfrac{20}{2028}\)
Vì \(\dfrac{20}{10005}\) < \(\dfrac{20}{2028}\) nên \(\dfrac{2005}{2001}\) < \(\dfrac{2020}{2028}\)