Bài 88: Gọi độ dài của cạnh tam giác vuông cân là: a (cm)  a > 0

             Theo pytago ta có: a² + a² = 2² 

                                             2a²       = 4

                                                a²       =   2

                                               \(\left[{}\begin{matrix}a=\sqrt{2}\\a=-\sqrt{2}\end{matrix}\right.\)

                                              vì a > 0  nên a = - \(\sqrt{2}\) (loại)

Độ dài cạnh góc vuông của tam giác vuông cân là \(\sqrt{2}\) cm

b, a² + a² = (\(\sqrt{2}\))²

    2a²       =     2

      a²       =      1

       \(\left[{}\begin{matrix}a=1\\a=-1\end{matrix}\right.\)

Vì a > 0 nên a = - 1 loại

Vậy cạnh góc vuông của tam giác vuông cân là 1 cm

Her children often play soccer in the afternoon.

children/ play/ soccer/ in the/ her/ often/ afternoon

\(\to\) Her children often play soccer in the afternoon

a. \(1+2+3+...+69+70\) 

Dãy số trên có số số hạng là:

\(\left(70-1\right):1+1=70\)(số hạng)

Tổng của dãy số trên là:

\(\left(70+1\right)\times70:2=2485\)

b. \(3+7+10+...+102+105\)

Dãy số trên có số số hạng là:

\(\left(105-3\right):3+1=35\)(số hạng)

Tổng của dãy số trên là:

\(\left(105+3\right)\times35:2=1890\)

a,số số hạng là:(70-1):1+1=70

tổng:(70+1)x70:2=2485

b,số số hạng là:(105-3):3+1=35

tổng:(105+3)x35:2=1890

F = {x \(\in\) N / \(x=4k+1;k\in N;\) 0 ≤ k ≤ 5 }

F = {x \(\in\) N / x = \(4k+1\); \(k\in N\); 0 ≤ k ≤ 5}

Tập hợp F có 6 phần tử

\(2.\left(2x-1\right)^2=50\\ \Rightarrow\left(2x-1\right)^2=50:2\\ \Rightarrow\left(2x-1\right)^2=25\\ \Rightarrow\left(2x-1\right)^2=\left(\pm5\right)^2\\ \Rightarrow\left[{}\begin{matrix}2x-1=5\\2x-1=-5\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}2x=6\\2x=-4\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=3\\x=-2\end{matrix}\right.\)

a) (2x - 5)² - (5 + 2x) = 0

<=> 4x² - 22x + 20 = 0 

\(\Leftrightarrow\left(2x-\dfrac{11}{2}\right)^2=\dfrac{41}{4}\)

\(\Leftrightarrow x=\dfrac{\pm\sqrt{41}+11}{4}\)

b) \(27x^3-54x^2+36x=0\)

\(\Leftrightarrow x\left(3x^2-6x+4\right)=0\)

\(\Leftrightarrow x=0\) (Vì \(3x^2-6x+4=3\left(x-1\right)^2+1>0\forall x\))

c) x³ + 8 - (x + 2).(x - 4) = 0

\(\Leftrightarrow\left(x+2\right).\left(x^2-2x+4\right)-\left(x+2\right)\left(x-4\right)=0\)

\(\Leftrightarrow\left(x+2\right)\left(x^2-3x+8\right)=0\)

\(\Leftrightarrow x=-2\) (Vì \(x^2-3x+8=\left(x-\dfrac{3}{2}\right)^2+\dfrac{23}{4}>0\))

d) \(x^6-1=0\)

\(\Leftrightarrow\left(x^2\right)^3-1=0\)

\(\Leftrightarrow\left(x^2-1\right)\left(x^4+x^2+1\right)=0\)

\(\Leftrightarrow x^2-1=0\) (Vì \(x^4+x^2+1>0\))

\(\Leftrightarrow x=\pm1\)

\(d,x^6-1=0\\ \Leftrightarrow\left(x^2\right)^3-1^3=0\\ \Leftrightarrow\left(x^2-1\right)\left(x^4+x^2+1\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x+1\right)\left(x^4+x^2+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-1=0\\x+1=0\\x^4+x^2+1=0\left(Vô.lí,vì:x^4\ge0;x^2\ge0,\forall x\in R\right)\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\\ c,\left(x^3+8\right)-\left(x+2\right)\left(x-4\right)=0\\ \Leftrightarrow\left(x^3+8\right)-\left(x^2-2x-8\right)=0\\ \Leftrightarrow x^3-x^2+2x+16=0\\ \Leftrightarrow x^3+2x^2-3x^2-6x+8x+16=0\\ \Leftrightarrow x^2\left(x+2\right)-3x\left(x+2\right)+8\left(x+2\right)=0\\ \Leftrightarrow\left(x^2-3x+8\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x^2-3x+8=0\left(Vô.lí\right)\\x+2=0\end{matrix}\right.\Leftrightarrow x=-2\)

\(\left(x-2\right)^m=\left(x-2\right)^{m+3}\)

\(\Rightarrow\left(x-2\right)^{m+3}-\left(x-2\right)^m=0\)

\(\Rightarrow\left(x-2\right)^m\left[\left(x-2\right)^3-1\right]=0\)

\(\Rightarrow\left[{}\begin{matrix}x-2=0\\\left(x-2\right)^3-1=0\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=2\\\left(x-2\right)^3=1^3\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=2\\x-2=1\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=2\\x=3\end{matrix}\right.\)

\(\Rightarrow x\in\left\{2;3\right\}\)

a) \(1.2+2.3+3.4+...+19.20\)

\(=\dfrac{20.\left(20+1\right).\left(20+2\right)}{3}\)

\(=3080\)

b) \(9+99+999+...+999...9\left(100so9\right)\)

\(\)\(=\left(10-1\right)+\left(100-1\right)+\left(1000-1\right)+...+\left(1000...0-1\right)\left(99so0\right)\)

\(=\left(10+10^2+10^3+...10^{99}\right)+\left(-1\right).100\)

\(=\left(1+10+10^2+10^3+...10^{99}\right)+\left(-1\right).101\)

\(=\dfrac{10^{99+1}-1}{99-1}-101\)

\(=\dfrac{10^{100}-1}{98}-101\)

\(=\dfrac{10^{100}-9899}{98}\)

c) \(999.9x222...2\) (100 số 9; 100 số 2)

\(9x2=18\)

\(99x22=2178\)

\(999x222=\text{221778}\)

\(9999x2222=22217778\)

\(99999x22222=2222177778\)

\(.........\)

Theo quy luật trên ta có 100 số 9 nhân 100 số 2:

\(999.9x222...2=222...21777...78\) (99 sô 2; 1 số 1; 99 số 7; 1 số 8)

Ta có :

\(AH^2=AB^2+BH^2\left(1\right)\) (Δ ABH vuông tại H)

\(AH^2=AC^2+CH^2\left(2\right)\) (Δ ACH vuông tại H)

\(\left(1\right),\left(2\right)\Rightarrow AB^2+BH^2=AC^2+CH^2\)

\(\Rightarrow CH^2=AB^2+BH^2-AC^2\)

\(\Rightarrow CH^2=81+676-121=636\)

\(\Rightarrow CH=\sqrt[]{636}=\sqrt[]{4.159}=2\sqrt[]{159}\left(cm\right)\)

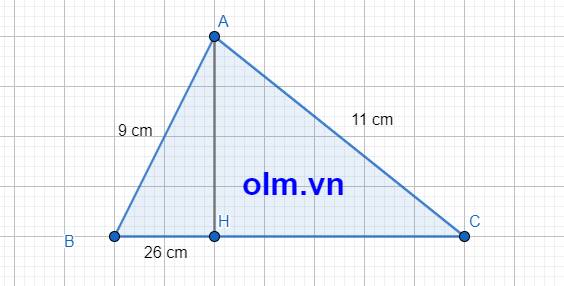
Vì AH là đường cao của tam giác ABC nên AH \(\perp\) BC \(\equiv\) H

⇒ \(\Delta\) AHB  \(\perp\)  \(\equiv\) H \(\Rightarrow\) AB > BH ⇒  9 cm > 26 cm vô lý

Em có hai sựa lựa chọn: 1 là em chỉ ra cái sai của cô

                                         2 là em xem lại đề bài của em