a) \(A=111...1555...56\) (n cs 1, n-1 cs 5)

\(A=111...1000...0+555...50+6\) (n cs 1, n cs 0 (không tính số 0 ở số 555...50), n-1 cs 5)

\(A=111...1.10^n+555...5.10+6\) (n cs 1, n-1 cs 5)

\(A=\dfrac{999...9}{9}.10^n+\dfrac{5}{9}.999...9.10+6\) (n cs 9 ở phân số thứ nhất, n-1 cs 9 ở phân số thứ 2)

\(A=\dfrac{10^n-1}{9}.10^n+\dfrac{5}{9}.\left(10^{n-1}-1\right).10+6\)

\(A=\dfrac{\left(10^n\right)^2-10^n+5.10^n-50+54}{9}\)

\(A=\dfrac{\left(10^n\right)^2+4.10^n+4}{9}\)

\(A=\left(\dfrac{10^n+2}{3}\right)^2\)

 Hiển nhiên \(3|10^n+2\) vì \(10^n+2\) có tổng các chữ số bằng 3, suy ra A là số chính phương.

Câu b áp dụng kĩ thuật tương tự nhé bạn.

Bài giải

Ta có sơ đồ như sau:

Tuổi mẹ: |-----|-----|-----|-----|

Tuổi con: |-----|

Theo sơ đồ, hiệu số phần bằng nhau là:

\(4-1=3\)(phần)

Tuổi của mẹ là:

\(30:3\times4=40\)(tuổi)

Tuổi của con là:

\(40-30=10\)(tuổi)

Đ/s: Mẹ: 40 tuổi; Con: 10 tuổi

Tuổi mẹ: |-----|-----|-----|-----|

Tuổi con: |-----|

Theo sơ đồ, hiệu số phần bằng nhau là:

$4-1=3$(phần)

Tuổi của mẹ là:

$30:3\times 4=40$(tuổi)

Tuổi của con là:

$40-30=10$(tuổi)

Đ/s: Mẹ: 40 tuổi; Con: 10 tuổi

`@nguyenngocbaochau`

|\(x\) + y - 7| + | \(x\) - 3| = 0

Vì |\(x\) + y - 7| ≥ 0; | \(x\) - 3| ≥ 0 ⇒ |\(x\) + y - 7| +| \(x\) - 3| = 0 

⇔\(\left\{{}\begin{matrix}x+y-7=0\\x-3=0\end{matrix}\right.\)

⇒ \(\left\{{}\begin{matrix}x=3\\y=4\end{matrix}\right.\)

Vậy cặp \(x\); y thỏa mãn đề bài là: (\(x;y\)) =( 3; 4)

Đề bài yêu cầu gì bạn ?

Đề yêu cầu gì thế em?

Ta có sơ đồ: 

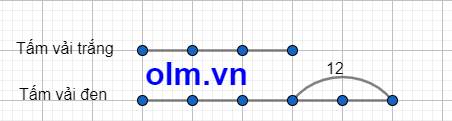
Theo sơ đồ ta có: Tấm vải trắng là: 12 : ( 5 - 3) \(\times\) 3 = 18 (m)

Tấm vải đen dài : 18 + 12 = 30 (m)

Đáp số: Vải trắng 18 m

              Vải đen 30 m 

Mình hỏi bài này với

a) \(\left(x+5\right).6-7=29\)

\(\Rightarrow\left(x+5\right).6=29+7\)

\(\Rightarrow\left(x+5\right).6=36\)

\(\Rightarrow\left(x+5\right)=36:6=6\)

\(\Rightarrow x=6-5=1\)

b) \(5x-3x=12-3.2\)

\(\Rightarrow2x=6\Rightarrow x=6:2=3\)

c) \(\dfrac{1}{4}.3< x< \dfrac{51}{50}.4\)

\(\Rightarrow\dfrac{3}{4}< x< \dfrac{102}{25}\)

a) \(\Delta ABE,\Delta ACF\) có \(\widehat{A}\) chung và \(\widehat{AEB}=\widehat{AFC}\left(=90^o\right)\) nên suy ra \(\Delta ABE~\Delta ACF\left(g.g\right)\) \(\Rightarrow\dfrac{AB}{AC}=\dfrac{AE}{AF}\Rightarrow AB.AF=AC.AE\).

b) Từ \(AB.AF=AC.AE\Rightarrow\dfrac{AE}{AB}=\dfrac{AF}{AC}\). Từ đó suy ra \(\Delta AEF~\Delta ABC\left(c.g.c\right)\) \(\Rightarrow\widehat{AFE}=\widehat{ACB}\)

c) Xét tam giác AEF có \(C\in AE,B\in AF,K\in EF\) và \(K,B,C\) thẳng hàng nên áp dụng định lý Menelaus, ta có \(\dfrac{KF}{KE}.\dfrac{CE}{CA}.\dfrac{BA}{BF}=1\)  (1).

 Mặt khác, cũng trong tam giác AEF, có \(C\in AE,B\in AF,I\in EF\) và AI, EB, FC đồng quy nên theo định lý Ceva, \(\dfrac{IF}{IE}.\dfrac{CE}{CA}.\dfrac{BA}{BF}=1\)   (2).

Từ (1) và (2), suy ra \(\dfrac{KF}{KE}=\dfrac{IF}{IE}\Leftrightarrow KF.IE=KE.IF\)

\(\dfrac{ }{ }\)

\(A=\dfrac{1}{2.2}+\dfrac{1}{3.3}+\dfrac{1}{4.4}+...+\dfrac{1}{2009.2009}\)

\(\dfrac{1}{2.2}< \dfrac{1}{1.2}=1-\dfrac{1}{2}\)

\(\dfrac{1}{3.3}< \dfrac{1}{2.3}=\dfrac{1}{2}-\dfrac{1}{3}\)

\(\dfrac{1}{4.4}< \dfrac{1}{3.4}=\dfrac{1}{3}-\dfrac{1}{4}\)

...

\(\dfrac{1}{2009.2009}< \dfrac{1}{2008.2009}=\dfrac{1}{2008}-\dfrac{1}{2009}\)

\(\Rightarrow A=\dfrac{1}{2.2}+\dfrac{1}{3.3}+\dfrac{1}{4.4}+...+\dfrac{1}{2009.2009}< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...\dfrac{1}{2008}-\dfrac{1}{2009}=1-\dfrac{1}{2009}< 1\)

\(\Rightarrow A=\dfrac{1}{2.2}+\dfrac{1}{3.3}+\dfrac{1}{4.4}+...+\dfrac{1}{2009.2009}< 1\)

Ta có:

\(\dfrac{1}{2\times2}+\dfrac{1}{3\times3}+\dfrac{1}{4\times4}+...+\dfrac{1}{2009\times2009}< \dfrac{1}{1\times2}+\dfrac{1}{2\times3}+\dfrac{1}{3\times4}+...+\dfrac{1}{2008\times2009}\\ =1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2008}-\dfrac{1}{2009}=1-\dfrac{1}{2009}< 1\)

a, 2 + 4 + 6 +...+ 2 \(\times\) n = 210

   A = 2 + 4 + 6 +...+ 2n

Dãy số trên là dãy số cách đều với khoảng cách là: 4 - 2 = 2.

Số số hạng của dãy số trên là: (2n - 2): 2 + 1 = n 

A = (2n + 2).n : 2  = (n+1).n

⇒ (n+1).n = 210 ⇒ (n+1).n = 14 \(\times\) 15 ⇒ n = 14

B, 1 + 3 + 5+...+ (2n - 1) = 225

B = 1 + 3 + 5 +...+ (2n - 1)

Dãy số trên là dãy số cách đều với khoảng cách là: 3 - 1 = 2

Số số hạng của dãy số trên là: ( 2n - 1 - 1): 2 + 1 = n 

B = (2n - 1+1).n : 2  = n.n

⇒n² = 225 ⇒ n² = 15² ⇒  \(\left[{}\begin{matrix}n=15\\n=-15\end{matrix}\right.\); n = -15 loại

Vậy n = 15