cho ab+cd chia hết cho 11. Chứng tỏ abcd chia hết cho 11
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đổi: 7,5km = 7500m
Người ta đã trải nhựa được số mét là:
\(7500\times32,5\div100=2437,5\left(m\right)\)
Đoạn đường chưa trải nhựa dài số mét là:
\(7500-2437,5=5062,5\left(m\right)\)
Đáp số: \(5062,5m\)

\(a,\dfrac{-8}{12}=\dfrac{-8:4}{12:4}=\dfrac{-2}{3}\\ Vì:\dfrac{-2}{3}=-\dfrac{2}{3}\Rightarrow-\dfrac{2}{3}=-\dfrac{8}{12}\\ b,\dfrac{48}{-40}=\dfrac{48:8}{-40:8}=\dfrac{6}{-5}\\ Vì:\dfrac{6}{-5}=\dfrac{6}{-5}\Rightarrow\dfrac{48}{-40}=\dfrac{6}{-5}\\ c,\dfrac{-42}{77}=\dfrac{-42:7}{77:7}=\dfrac{-6}{11}\\ Vì:\dfrac{-6}{11}=\dfrac{-6}{11}\Rightarrow\dfrac{-42}{77}=\dfrac{-6}{11}\)

\(a,2^4.2^5=2^{4+5}=2^9\\ b,5^{12}:5^6=5^{12-6}=5^6\\ c,7^5:\left(7.7^2\right)=7^5:7^{1+2}=7^5:7^3=7^{5-3}=7^2\\ d,9.3^7:3^0=3^2.3^7:3^0=3^{2+7-0}=3^9\)

\(P=3sin^22a+4cos^22a\)
\(\Rightarrow P=3sin^22a+3cos^22a+cos^22a\)
\(\Rightarrow P=3\left(sin^22a+cos^22a\right)+\left(2cos^2a-1\right)^2\)
\(\Rightarrow P=3.1+\left(2.\dfrac{1}{9}-1\right)^2\left(cosa=\dfrac{1}{3}\right)\)
\(\Rightarrow P=3+\left(-\dfrac{7}{9}\right)^2\)
\(\Rightarrow P=3+\dfrac{49}{81}\)
\(\Rightarrow P=\dfrac{292}{81}\)


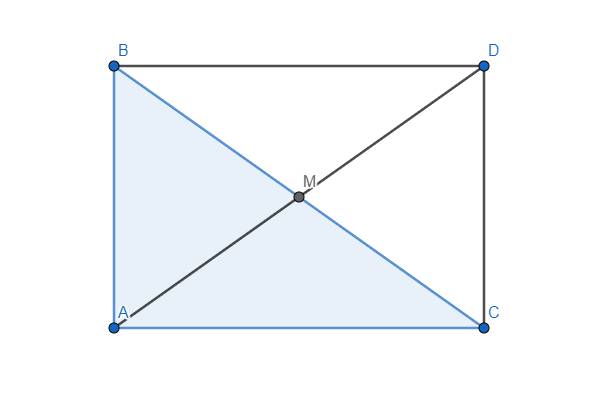
Trên tia đối của tia MA lấy điểm D sao cho \(MD=MA\). Khi đó xét 2 tam giác MAB và MDC, ta có \(MA=MD\) (cách vẽ), \(\widehat{AMB}=\widehat{DMC}\) và \(MB=MC\) (do AM là đường trung tuyến của tam giác ABC)
\(\Rightarrow\Delta MAB=\Delta MDC\left(c.g.c\right)\) \(\Rightarrow\widehat{MAB}=\widehat{MDC}\) \(\Rightarrow AB//CD\). Mà \(AB\perp AC\) nên \(AC\perp CD\) hay \(\widehat{ACD}=90^o\)
Đồng thời ta cũng có \(AB=CD\)
Xét 2 tam giác ABC và CDA, có AC là cạnh chung, \(\widehat{BAC}=\widehat{DCA}\left(=90^o\right)\) và \(AB=CD\left(cmt\right)\), suy ra \(\Delta ABC=\Delta CDA\left(c.g.c\right)\) \(\Rightarrow BC=AD\)
\(\Rightarrow\dfrac{1}{2}BC=\dfrac{1}{2}AD\) \(\Rightarrow MB=MA\)
Từ đó ta có \(MA=MB=MC=MD\), suy ra đpcm.

Tính số chẵn là sao em nhỉ? Em có thể mô tả rõ đề hơn được không?
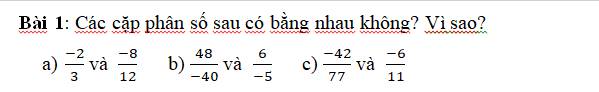 giúp mik với nha ^^
giúp mik với nha ^^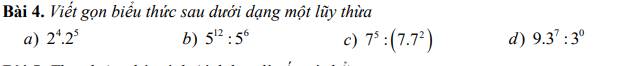
Một số chia hết cho 11 khi hiệu giữa tổng các chữ số ở vị trí chẵn (hoặc lẻ) với tổng các chữ số ở vị trí lẻ (hoặc chẵn) chia hết cho 11
\(\overline{abcd}⋮11\) khi \(\left(a+c\right)-\left(b+d\right)⋮11\) hoặc \(\left(b+d\right)-\left(a+c\right)⋮11\)
Ta có
\(\overline{ab}+\overline{cd}=10.a+b+10.c+d=\)
\(=11.a+11.c+\left(b+d\right)-\left(a+c\right)=\)
\(=11.\left(a+c\right)+\left(b+d\right)-\left(a+c\right)⋮11\)
Ta có \(11.\left(a+c\right)⋮11\Rightarrow\left(b+d\right)-\left(a+c\right)⋮11\)
\(\Rightarrow\overline{abcd}⋮11\)