
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vận tốc xe đi từ A -> B: 25km/h
Vận tốc xe đi từ B-> A:25 x 2 = 50km/h
Vì vận tốc đi từ B->A gấp 2 lần vận tốc đi từ A->B
=> Thời gian đi từ B->A chỉ bằng 1/2 thời gian đi từ A->B
Tổng số phần bằng nhau:
2+1=3(phần)
Thời gian xe máy đi từ B->A bằng:
3:3 x 1=1(giờ)
Quãng đường AB dài:
1 x 50=50(km)
Đ.số: 50km
Cách này phù hợp tiểu học
Gọi quãng đường AB là x km.
Khoảng thời gian đi từ A đến B bằng xe máy là:
t1 = x/25 (giờ)
Khoảng thời gian đi từ B về A bằng ô tô là:
t2 = x / (2 * 25) = x / 50 (giờ)
Tổng thời gian cả đi và về là:
t = t1 + t2 = x/25 + x/50 = (2x + x)/50 = 3x/50 = 3x/50 = 3/50 * x (giờ)
Vì tổng thời gian là 3 giờ, nên ta có:
3/50 * x = 3
x = 50
Vậy quãng đường AB là 50 km.

Chứng minh: Số có dạng \(n^6-n^4+2n^3+2n^2\) với \(n\inℕ\) và \(n>1\) không phải là số chính phương.

\(=n^2\left(n^4-n^2+2n+2\right)=\)
\(=n^2\left[n^2\left(n^2-1\right)+2\left(n+1\right)\right]=\)
\(=n^2\left[n^2\left(n-1\right)\left(n+1\right)+2\left(n+1\right)\right]=\)
\(=n^2\left[\left(n+1\right)\left(n^3-n^2+2\right)\right]=\)
\(=n^2\left\{\left(n+1\right)\left[\left(n^3+1\right)-\left(n^2-1\right)\right]\right\}=\)
\(=n^2\left\{\left(n+1\right)\left[\left(n^3+1\right)-\left(n-1\right)\left(n+1\right)\right]\right\}=\)
\(=n^2\left\{\left(n+1\right)\left[\left(n+1\right)\left(n^2-n+1\right)-\left(n-1\right)\left(n+1\right)\right]\right\}=\)
\(=n^2\left(n+1\right)^2\left(n^2-n+1\right)-n^2\left(n+1\right)^2\left(n-1\right)=\)
\(=n^2\left(n+1\right)^2\left[\left(n^2-n+1\right)-\left(n-1\right)\right]=\)
\(=n^2\left(n+1\right)^2\left(n^2-2n+2\right)\) Giả sử đây là số chính phương
\(\Rightarrow n^2-2n+2\) Phải là số chính phương
Ta có
\(n^2-2n+2=\left(n-1\right)^2+1\Rightarrow n^2-2n+2>\left(n-1\right)^2\) (1)
Ta có
\(n^2-2n+2=n^2-2\left(n-1\right)\) Với n>1
\(\Rightarrow n^2-2n+2< n^2\) (2)
Từ (1) và (2)
\(\Rightarrow\left(n-1\right)^2< n^2-2n+2< n^2\)
Mà \(\left(n-1\right)^2\) và \(n^2\) là hai số chính phương liên tiếp nên \(n^2-2n+2\) không phải là số chính phương
=> Biểu thức đề bài đã cho không phải là số chính phương

Ok em, để olm.vn giúp em nhá:
A = \(\dfrac{1}{2}\):3 + \(\dfrac{1}{3}\):4 + \(\dfrac{1}{4}\):5+...+\(\dfrac{1}{2018}\):2019 + \(\dfrac{1}{2019}\): 2020
A=\(\dfrac{1}{2}\times\dfrac{1}{3}+\dfrac{1}{3}\times\dfrac{1}{4}+\dfrac{1}{4}\times\dfrac{1}{5}+..+\dfrac{1}{2018}\times\dfrac{1}{2019}+\dfrac{1}{2019}\times\dfrac{1}{2020}\)
A = \(\dfrac{1}{2}\) - \(\dfrac{1}{3}\) + \(\dfrac{1}{3}\) - \(\dfrac{1}{4}\) + \(\dfrac{1}{4}\) - \(\dfrac{1}{5}\)+....+ \(\dfrac{1}{2018}\) - \(\dfrac{1}{2019}\)+ \(\dfrac{1}{2019}\) - \(\dfrac{1}{2020}\)
A = \(\dfrac{1}{2}\) - \(\dfrac{1}{2020}\)
A = \(\dfrac{1009}{2020}\)

\(\dfrac{1}{2}-\dfrac{1}{2}\left(3-2x\right)=0\)
\(\Rightarrow\dfrac{1}{2}\left[1-\left(3-2x\right)\right]=0\)
\(\Rightarrow\dfrac{1}{2}\left[1-3+2x\right]=0\)
\(\Rightarrow\dfrac{1}{2}\left[2x-2\right]=0\)
\(\Rightarrow2x-2=0\Rightarrow2x=2\Rightarrow x=1\)

Từ 6/8/2020 - 6/8/2025 có 1 năm nhuận, 4 năm không nhuận
Tổng số ngày trong 5 năm này:
365 x 5 + 1=1826(ngày)
Ta có: 1826:7= 260 (dư 6)
Vậy ngày 6/8/2025 là thứ 4.

Kéo dài AB cắt Cy tại E và kéo dài CB cắt Ax tại G như hình vẽ dưới đây:
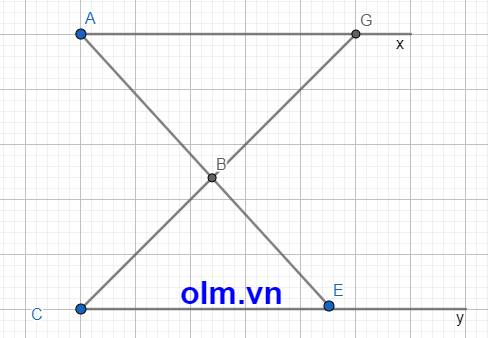
\(\widehat{ABC}\) = \(\widehat{GBE}\) (1) (vì đối đỉnh)
\(\widehat{GBE}\) = \(\widehat{BCE}\) + \(\widehat{CEB}\) (2) ( vì góc ngoài của tam giác bằng tổng hai góc trong không kề với nó)
\(\widehat{ABC}\) = \(\widehat{GAB}\) + \(\widehat{BCE}\) (3)
Từ (1); (2); (3) ta có: \(\widehat{BCE}\) + \(\widehat{CEB}\) = \(\widehat{GAB}\) + \(\widehat{BCE}\)
⇒ \(\widehat{CEB}\) = \(\widehat{GAB}\)
Mà hai góc CEB và góc GAB là hai góc ở vị trí so le trong nên
Cy // Ax (đpcm)

\(\left(\dfrac{1}{2}-1\right)\left(\dfrac{1}{3}-1\right)...\left(\dfrac{1}{2008}-1\right)\left(\dfrac{1}{2009}-1\right)\\ =-\dfrac{1}{2}.\left(-\dfrac{2}{3}\right)...\left(-\dfrac{2007}{2008}\right)\left(-\dfrac{2008}{2009}\right)\\ =\dfrac{1}{2}.\dfrac{2}{3}...\dfrac{2007}{2008}.\dfrac{2008}{2009}\\ =\dfrac{1.2...2007.2008}{2.3...2008.2009}=\dfrac{1}{2009}\)
\(\left(\dfrac{1}{2}-1\right)\left(\dfrac{1}{3}-1\right)...\left(\dfrac{1}{2008}-1\right)\left(\dfrac{1}{2009}-1\right)\)
`=`\(\left(\dfrac{1}{2}-\dfrac{2}{2}\right)\left(\dfrac{1}{3}-\dfrac{3}{3}\right)...\left(\dfrac{1}{2008}-\dfrac{2008}{2008}\right)\left(\dfrac{1}{2009}-\dfrac{2009}{2009}\right)\)
`=`\(-\dfrac{1}{2}\cdot\left(-\dfrac{2}{3}\right)\cdot...\cdot\left(-\dfrac{2007}{2008}\right)\cdot\left(-\dfrac{2008}{2009}\right)\)
`=`\(-\dfrac{1}{2009}\)
Diện tíc mảnh đất hình chữ nhật là:
12 x 10 = 120 (m2)
Phần đất trồng cỏ là:
(10 x 6 : 2) x 2 = 60 (m2)
Phần đất trồng hoa là
120 - 60 = 60 (m2)
Số tiền công cần chi trả để trồng hoa là
50000 x 60 = 3 000 000 (đồng)
Số tiền công cần chi trả để trồng cỏ là
40000x 60 = 2 400 000 (đồng)
Số tiền công cần chi trả để trồng hoa và cỏ là
3000000 + 2400000 = 5400000(đồng)
Đáp số 5400000 đồng
Diện tích hình thoi là
5 . 8 : 2 = 20 (m2)
Cần số cây hoa để trồng trên mảnh đất hình thoi là
20x 4 = 80 (cây)
Đáp số 80 cây