Giải giúp em vs ạ
(x+5)^2-4x^2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
$2x^3y+2xy^3+4x^2y^2-8xy$
$=2xy(x^2+y^2+2xy-4)$
$=2xy[(x^2+2xy+y^2)-4]$
$=2xy[(x+y)^2-2^2]=2xy(x+y-2)(x+y+2)$
P.s: lần sau bạn lưu ý ghi đầy đủ yêu cầu đề.

1 B
2 D
3 C
4 A
5 C
VII
1 Although she is careful, she still forgets her phone when she goes out

\((2x-5)^2-64x^2\\=(2x-5)^2-(8x)^2\\=(2x-5-8x)(2x-5+8x)\\=(-6x-5)(10x-5)\)
Lời giải:
$(2x-5)^2-64x^2=(2x-5)^2-(8x)^2$
$=(2x-5-8x)(2x-5+8x)$
$=(-6x-5)(10x-5)$
$=-5(6x+5)(2x-1)$

c, \(x\)(\(x\) - 2022) + 4.(2022 - \(x\)) = 0
(\(x\) - 2022).(\(x\) - 4) = 0
\(\left[{}\begin{matrix}x-2022=0\\x+4=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=2022\\x=4\end{matrix}\right.\)

#include <iostream>
#include <vector>
using namespace std;
vector<int> solve(int d) {
vector<int> res(2, 0);
int p = 1;
while (d > 0) {
int digit = d % 10;
d /= 10;
if (digit == 4) {
res[0] += p * 3;
res[1] += p;
} else {
res[0] += p * digit;
}
p *= 10;
}
return res;
}
int main() {
int d;
cin >> d;
vector<int> res = solve(d);
cout << res[0] << " " << res[1] << endl;
return 0;
}

Có 4 cách chọn thẻ thứ nhất. có 3 cách chọn thẻ thứ hai số cách chọn 2 tấm thẻ khác nhau từ 4 tấm thẻ là:
4 x 3 = 12 (cách)
Theo cách tính trên mỗi cách đã được tính hai lần. Vậy số cách lấy được 2 tấm thẻ từ bốn tấm thẻ đã cho là:
12 : 2 = 6 (cách)
Có 2 cách chọn tấm thẻ thứ nhất, có 3 cách chọn thẻ thứ hai. Vậy số cách chọn hai tấm thẻ để tích các số trên hai thẻ rút ra là số chẵn" là:
2 x 3 = 6 (cách)
Theo cách tính trên mỗi cách đã được tính hai lần.
Vậy số cách để rút hai tấm thẻ mà tích các số trên hai thẻ là số chẵn là:
6 : 2 = 3 (cách)
Xác suất của biến cố "tích các số trên hai thẻ rút ra là số chẵn" là:
3 : 6 = \(\dfrac{1}{2}\)
Kết luận:...
Cách thứ hai: Số cách chọn 2 thẻ bất kì (có kể thứ tự) là \(4.3=12\) cách. Như vậy, số cách chọn 2 thẻ không tính thứ tự là \(\dfrac{12}{2}=6\) cách.
Ta xét biến cố A: "Tích 2 số trên 2 thẻ rút ra là số chẵn." Biến cố đối của nó là \(\overline{A}\): "Tích 2 số trên 2 thẻ rút ra là số lẻ." Biến cố này tương đương với biến cố: "Cả 2 số trên 2 thẻ rút được là số lẻ."
Ta thấy trường hợp duy nhất thỏa mãn là rút được 2 tấm thẻ số 5 và 7. \(\Rightarrow P\left(\overline{A}\right)=\dfrac{1}{6}\) \(\Rightarrow P\left(A\right)=\dfrac{5}{6}\)
Vậy xác suất của biến cố: "Tích các số trên 2 thẻ rút ra là số chẵn." là \(\dfrac{5}{6}\).


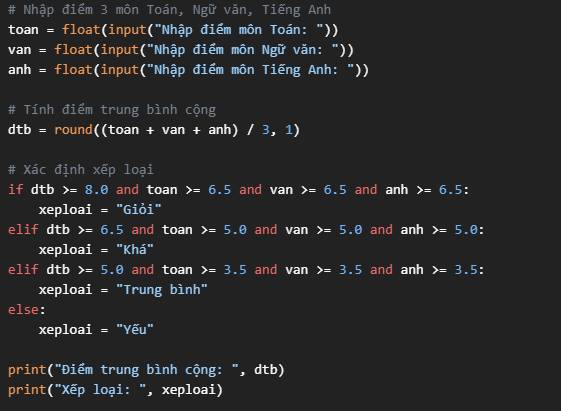
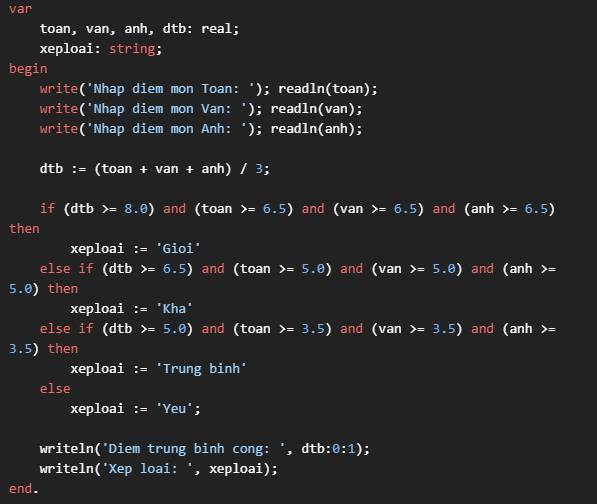


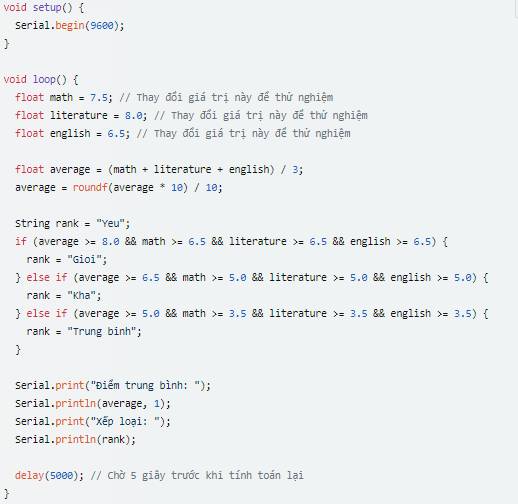

\((x+5)^2-4x^2\\=(x+5)^2-(2x)^2\\=(x+5-2x)(x+5+2x)\\=(5-x)(3x+5)\)