cho tam giác ABC cân tại A. Gọi H là trung điểm của BC.
a) chứng minh tam giác ABH= tam giác ACH.
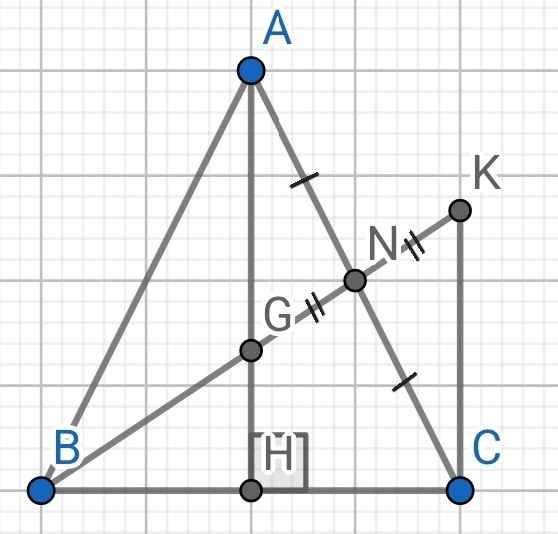
b) Trên tia đối HA lấy điểm M sao cho HM=HA. Chứng minh MC// AB.
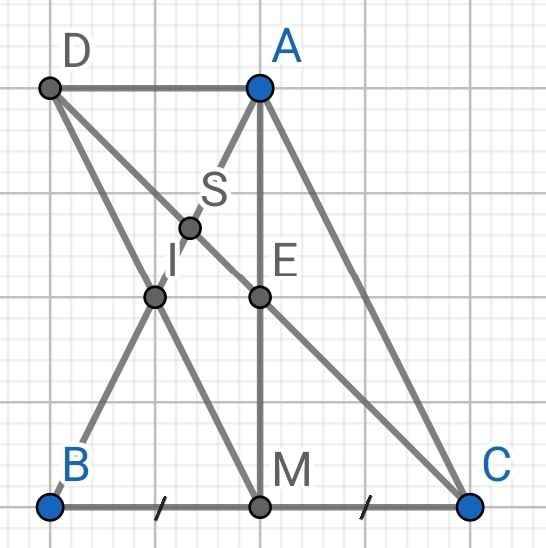
c) Gọi E ; F lần lượt là trung điểm của AC và MC; G là giao điểm của À và BC. Chứng minh 3 điểm M, G, E thẳng hàng.

a)Xét 2 tam giác ABH và ACH có:
AB=AC(do tam giác ABC cân tại A)
Góc ABC bằng góc ACB (do tam giác ABC cân tại A)
BH=HC(H là trung điểm BC)
=>Tam giác ABH = tam giác ACH(cạnh - góc - cạnh)
b)Xét 2 tam giác HBA và HCM có:
Góc AHB bằng góc CHM(2 góc đối đỉnh)
HA=HM(giả thiết)
BH=HC(H là trung điểm BC)
=>Tam giác HBA bằng tam giác HCM(cạnh-góc-cạnh)
=>Góc ABH=góc MCH(2 góc tương ứng)
mà 2 góc này nằm ở vị trí so le trong của đường thẳng AB và MC nên MC//AB
c)Xét tam giác ACM có:
CH là đường trung tuyến(H là trung điểm AM)
AF là đường trung tuyến(F là trung điểm MC)
Mà AF cắt CH tại G(do AF cắt BC tại G;H thuộc BC;G thuộc CH)
=>G là trọng tâm của tam giác ACM
Ta có:
ME cũng là 1 đường trung tuyến của tam giác ACM (E là trung điểm AC)
=>G thuộc ME ( tính chất 3 đường trung tuyến)
=>M,G,E thẳng hàng
`#3107.101107`
`a)`
Vì `\triangle ABC` cân tại A
`\Rightarrow`\(\text{AB = AC; }\widehat{\text{ABC}}=\widehat{\text{ACB}}\)
Xét `\triangle ABH` và `\triangle ACH`:
`\text{AB = AC}`
\(\widehat{\text{ABC}}=\widehat{\text{ACB}}\)
\(\text{HB = HC (H là trung điểm BC)}\)
\(\Rightarrow\) `\triangle ABH = \triangle ACH (c - g - c)`
`b)`
Xét `\triangle AHB` và `\triangle MHC`:
\(\text{AH = HM}\)
\(\widehat{\text{AHB}}=\widehat{\text{MHC}}\left(\text{đối đỉnh}\right)\)
\(\text{HB = HC }\)
`\Rightarrow \triangle AHB = \triangle MHC (c-g-c)`
\(\Rightarrow\widehat{\text{ABH}}=\widehat{\text{MCH}}\left(\text{2 góc tương ứng}\right)\)
Mà `2` góc này nằm ở vị trí sole trong
\(\Rightarrow\text{ }\text{MC // AB (tính chất)}\)
`c)`
Vì E là trung điểm của AC; F là trung điểm của MC
\(\Rightarrow\text{EA = EC; FM = FC}\)
Ta có:
\(\left\{{}\begin{matrix}\text{EA = EC}\\\text{FM =FC}\\\text{HA = HM}\end{matrix}\right.\)
\(\Rightarrow\text{AF; ME và CH}\) lần lượt là các đường trung tuyến của `\triangle ACM`
Mà AF cắt HC tại G
\(\Rightarrow\) G là trọng tâm của `\triangle ACM`
\(\Rightarrow\) \(\text{G}\in\text{ME}\)
\(\Rightarrow\) `3` điểm M, G, E thẳng hàng (đpcm).