Đáp án :C.48 

20% của 240 là: 

\(20.\dfrac{240}{100}=48\)

Dấu"."bằng dấu"x" nha!

Lời giải:

20% của 240 là:

$240\times 20:100=48$

Đáp án C.
 

Lời giải:

Thời gian nhà bạn Minh đi quãng đường từ HCM đến Mũi Né (không kể thời gian nghỉ) là:

12 giờ 10 phút - 7 giờ 30 phút - 34 phút = 4 giờ 40 phút = 4 giờ 6 phút = 4,1 giờ

Quãng đường từ HCM đến Mũi Né dài:

$4,1\times 56=229,6$ (km)

            Giải:

a;          \(\dfrac{40}{100}\) = \(\dfrac{2}{5}\) 

 Tổng độ dài hai đáy là:

           70 x 2 = 140 (m)

 Ta có sơ đồ:

 Theo sơ đồ ta có:

   Đáy lớn của mảnh vườn hình thang là: 140:  (2 + 5) x 5 = 100 (m)

   Đáy bé của mảnh vườn hình thang là: 140 - 100 = 40 (m)

  Chiều cao của mảnh vườn hình thang là: 100 x \(\dfrac{5}{4}\) = 125 (m)

   Diện tích của mảnh vườn hình thang là: 

       (100 + 40) x 125 : 2  = 8750 (m²)

  b; Phần diện tích còn lại chiếm số phần trăm là:

          100% - 30,5% = 69,5% 

  Diện tích còn lại là:

           8750 x 69,5 : 100 = 6081,25 (m²)

Đáp số: 

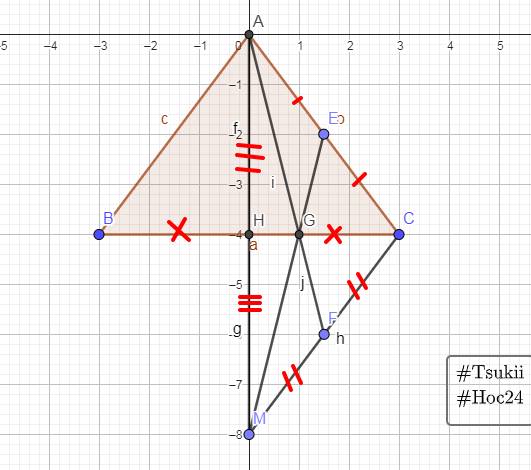
a)Xét 2 tam giác ABH và ACH có:
AB=AC(do tam giác ABC cân tại A)
Góc ABC bằng góc ACB (do tam giác ABC cân tại A)
BH=HC(H là trung điểm BC)
=>Tam giác ABH = tam giác ACH(cạnh - góc - cạnh)
b)Xét 2 tam giác HBA và HCM có:
Góc AHB bằng góc CHM(2 góc đối đỉnh)
HA=HM(giả thiết)
BH=HC(H là trung điểm BC)
=>Tam giác HBA bằng tam giác HCM(cạnh-góc-cạnh)
=>Góc ABH=góc MCH(2 góc tương ứng)
mà 2 góc này nằm ở vị trí so le trong của đường thẳng AB và MC nên MC//AB
c)Xét tam giác ACM có:
CH là đường trung tuyến(H là trung điểm AM)
AF là đường trung tuyến(F là trung điểm MC)
Mà AF cắt CH tại G(do AF cắt BC tại G;H thuộc BC;G thuộc CH)
=>G là trọng tâm của tam giác ACM
Ta có:
ME cũng là 1 đường trung tuyến của tam giác ACM (E là trung điểm AC)
=>G thuộc ME ( tính chất 3 đường trung tuyến)
=>M,G,E thẳng hàng 

`#3107.101107`

`a)`

Vì `\triangle ABC` cân tại A

`\Rightarrow`\(\text{AB = AC; }\widehat{\text{ABC}}=\widehat{\text{ACB}}\)

Xét `\triangle ABH` và `\triangle ACH`:

`\text{AB = AC}`

\(\widehat{\text{ABC}}=\widehat{\text{ACB}}\)

\(\text{HB = HC (H là trung điểm BC)}\)

\(\Rightarrow\) `\triangle ABH = \triangle ACH (c - g - c)`

`b)`

Xét `\triangle AHB` và `\triangle MHC`:

\(\text{AH = HM}\)

\(\widehat{\text{AHB}}=\widehat{\text{MHC}}\left(\text{đối đỉnh}\right)\)

\(\text{HB = HC }\)

`\Rightarrow \triangle AHB = \triangle MHC (c-g-c)`

\(\Rightarrow\widehat{\text{ABH}}=\widehat{\text{MCH}}\left(\text{2 góc tương ứng}\right)\)

Mà `2` góc này nằm ở vị trí sole trong

\(\Rightarrow\text{ }\text{MC // AB (tính chất)}\)

`c)`

Vì E là trung điểm của AC; F là trung điểm của MC

\(\Rightarrow\text{EA = EC; FM = FC}\)

Ta có:

\(\left\{{}\begin{matrix}\text{EA = EC}\\\text{FM =FC}\\\text{HA = HM}\end{matrix}\right.\)

\(\Rightarrow\text{AF; ME và CH}\) lần lượt là các đường trung tuyến của `\triangle ACM`

Mà AF cắt HC tại G

\(\Rightarrow\) G là trọng tâm của `\triangle ACM`

\(\Rightarrow\) \(\text{G}\in\text{ME}\)

\(\Rightarrow\) `3` điểm M, G, E thẳng hàng (đpcm).

a, Xét \(\Delta HBA\) và \(\Delta ABC\) có:

\(\left\{{}\begin{matrix}\widehat{BHA}=\widehat{BAC}=90^{\circ}\left(AH\bot BC;\Delta ABC\text{ vuông tại }A\right)\\\widehat{ABC}\text{ chung}\end{matrix}\right.\)

\(\Rightarrow \Delta HBA\backsim \Delta ABC(g.g)\)

b, Vì \(\Delta HBA\backsim \Delta ABC(cmt)\Rightarrow \widehat{HAB}=\widehat{ACB}\) (hai góc tương ứng)

hay \(\widehat{HAB}=\widehat{HCA}\) (do \(H\in BC\)>)>

Xét \(\Delta AHB\) và \(\Delta CHA\) có: \(\left\{{}\begin{matrix}\widehat{AHB}=\widehat{CHA}=90^{\circ}\left(AH\bot BC\right)\\\widehat{HAB}=\widehat{HCA}\left(cmt\right)\end{matrix}\right.\)

\(\Rightarrow \Delta AHB\backsim \Delta CHA(g.g)\Rightarrow \dfrac{AH}{CH}=\dfrac{HB}{HA}\) (các cạnh tương ứng)

\(\Rightarrow AH^2=HB\cdot HC\)

Hàm số bậc nhất có dạng: y = a\(x\) + b

Vì hệ số góc là - 3 nên a = -3 hàm số có dạng:

                      y = - 3\(x\) + b (d)

Vì hàm số cắt trục hoành tại đểm có hoành độ bằng 2 nên hàm số đó đi qua điểm A(2; 0).

Thay tọa độ điểm A vào phương trình đường thẳng d ta có 

                    -3.2 + b  = 0

                    -6 + b = 0

                            b = 6

Vậy hàm số có hệ số góc bằng -3 và cắt trục hoành có hoành độ bằng 2 có phương trình là:

                     y = -3\(x\) + 6

Bạn tham khảo thử nhé.

def sum_multiples_of_4(numbers):
    total = 0
    for num in numbers:
        if num % 4 == 0:
            total += num
    return total

# Nhập danh sách từ người dùng
n = int(input("Nhập số phần tử của danh sách: "))
B = []
for i in range(n):
    num = int(input(f"Nhập phần tử thứ {i+1}: "))
    B.append(num)

# Tính tổng và in ra màn hình
result = sum_multiples_of_4(B)
print("Tổng các số là bội của 4 trong danh sách là:", result)

     Nếu đề cho là tuần đầu tiên người đó xử lí \(\dfrac{1}{4}\) số báo cáo và tuần tiếp xử lí được \(\dfrac{1}{2}\) số báo cáo thì làm như sau:

                                  Giải:

  Số báo cáo người đó còn phải xử lí sau hai tuần ứng với phân số là:

                     1 - \(\dfrac{1}{4}\) - \(\dfrac{1}{2}\)  =  \(\dfrac{1}{4}\) (số báo cáo)

Sau hai tuần, số báo cáo mà người đó còn phải xử là:

                         120 x \(\dfrac{1}{4}\) = 30 (báo cáo)

Đáp số: 30 báo cáo. 

Nguyễn thị thương hoài .sau tuần 1 làm gì còn 120 báo cáo nữa cô ơi.

   A = \(\dfrac{3n+2}{7n+1}\) (n \(\in\) N)

Gọi ƯCLN(3n + 2; 7n + 1) = d

Ta có:  \(\left\{{}\begin{matrix}\left(3n+2\right).7⋮d\\\left(7n+1\right).3⋮d\end{matrix}\right.\)

            \(\left\{{}\begin{matrix}21n+14⋮d\\21n+3⋮d\end{matrix}\right.\)

            \(\left\{{}\begin{matrix}21n+14⋮d\\21n+14-21n-3⋮d\end{matrix}\right.\)

              \(\left\{{}\begin{matrix}21n+14⋮d\\11⋮d\end{matrix}\right.\)

d \(\in\) Ư(11) = {1; 11}

      \(\left\{{}\begin{matrix}3n+2⋮11\\7n+1⋮11\end{matrix}\right.\)

        \(\left\{{}\begin{matrix}3n+2⋮11\\2.\left(3n+2\right)+n-3⋮11\end{matrix}\right.\)

          n - 3 ⋮ 11

A = \(\dfrac{3n+2}{7n+1}\) tối giản khi và chỉ khi n - 3 \(\ne\)  11k (k \(\in\) N)

   n \(\ne\) 11k + 3 (k \(\in\) N)