Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Với mọi dãy (xn):xn>1
\(\forall\)n và \(limx_n=1\)ta có \(lim_{x\rightarrow1^+}\frac{4x-3}{x-1}=lim\frac{4x_n-3}{x_n-1}=+\infty\)

Đặt f(x)=cosx.
Chọn hai dãy số {xn} và {yn} với :
* xn=2nπ⇒xn→+∞ khi n→+∞ và ta được :
f(xn)=cos(xn)=cos(2nπ)=n→+∞1 .
* yn=π2+nπ⇒yn→+∞ khi n→+∞ và ta được :
f(yn)=cos(yn)=cos(π2+nπ)=n→+∞0.
Vậy limx→∞cosx không tồn tại.
Hai câu kia của mình bị lỗi ,không biết câu này có bị không
Đặt f(x)=cosx.
Chọn hai dãy số {xn} và {yn} với :
* xn=2nπ⇒xn→+∞ khi n→+∞ và ta được :
f(xn)=cos(xn)=cos(2nπ)=n→+∞1 .
* yn=π2+nπ⇒yn→+∞ khi n→+∞ và ta được :
f(yn)=cos(yn)=cos(π2+nπ)=n→+∞0.
Vậy limx→∞cosx không tồn tại.
Hai câu kia mình bị lỗi nha.

\(\hept{\begin{cases}lim_{x\rightarrow3^+}\frac{\left|x-3\right|}{x-3}=lim_{x\rightarrow3^+}\frac{x-3}{x-3}=1\\lim_{x\rightarrow3^-}\frac{\left|x-3\right|}{x-3}=lim_{x\rightarrow3^-}\frac{-x+3}{x-3}=-1\end{cases}\Rightarrow lim_{x\rightarrow3^+}\frac{\left|x-3\right|}{x-3}\ne lim_{x\rightarrow3^-}\frac{\left|x-3\right|}{x-3}}\)
=> đpcm

Ta có limx→0−f(x)=limx→0−(mx+m+14)=m+14limx→0−f(x)=limx→0−(mx+m+14)=m+14.
limx→0+f(x)=limx→0+√x+4−2x=limx→0+x+4−4x(√x+4+2)=limx→0+1√x+4+2=14limx→0+f(x)=limx→0+x+4−2x=limx→0+x+4−4x(x+4+2)=limx→0+1x+4+2=14.
Để hàm số có giới hạn tạix=0x=0 thì limx→0−f(x)=limx→0+f(x)⇔m+14=14⇔m=0limx→0−f(x)=limx→0+f(x)⇔m+14=14⇔m=0.

S A B C D K
gọi K thuộc SC sao cho DK \(\perp\) SC , BK \(\perp\)SC
=> ((SCD),(SBC)) = (DK,KB)
tính được SD = \(\frac{\sqrt{10}}{2}\)a, AC = \(\sqrt{3}\)a, SC= \(\frac{3\sqrt{2}}{2}\)a
\(DC^2=SD^2+SC^2-2SD.SC.cos\widehat{DSC}\)
=> \(\widehat{DSC}\)=....... (số xấu)
\(sin\widehat{DSC}\)= \(\frac{DK}{SD}\)=> DK = \(\frac{\sqrt{2}}{2}\)=BK
\(DB^2=DK^2+BK^2-2.DK.BK.cos\alpha\)=> \(\alpha=\frac{\pi}{2}\)





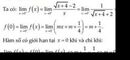
Gọi M, N lần lượt là trung điểm các cạnh AB và CD.
Ta có tam giác ANB cân tại N,
-> MN vuông góc AB.
Tam giác ADB = Tam giác ACB, ta có:
MD=MC -> Tam giác MDC cân tại M.
-> MN vuông góc CD
Do đó ta suy ra MN là đoạn vuông góc chung của cạnh AB và CD.
Ta có khoảng cách từ cạnh AB đến CD là MN:
MN= căn bậc a (AN^2-AM^2)= √2/2
Đáp số: khoảng cách giữa cạnh AB và CD là √2/2
Gọi M và N lần lượt là trung điểm của AB và CD. Khi đó:
\(\Delta ACD\)và \(\Delta BCD\)là 2 tam giác đều cạnh 3 nên AN=BN=\(\frac{3\sqrt{3}}{2}\)
Đồng thời \(\Delta ABC=\Delta ABD\)nên CM=DM
Do đó MAB và NCD là 2 tam giác cân tại M và N
Vậy MN _|_ BA và MN _|_ CD
Ta có MN=\(\sqrt{NB^2-MB^2}=\sqrt{\frac{27}{4}-\frac{25}{4}}=\frac{\sqrt{2}}{2}\)