Số cây đội 2 trồng được là :

\(3564-558=3006\left(cây\right)\)

Số cây đội  trồng được là :

\(\left(3006+3564\right).\dfrac{1}{3}=2190\left(cây\right)\)

Trung bình mỗi đội trồng được là :

\(\left(3564+3006+2190\right):3=2920\left(cây\right)\)

Đội 2 trồng được là: 3564 - 558 = 3006 (cây)

Tổng số cây đội 1 và đội 2 trồng được là: 3564 + 3006 = 6570 (cây)

Đội 3 trồng được là:  6570 \(\times\) \(\dfrac{1}{3}\) = 2190 (cây)

Trung bình mỗi đội trồng được số cây là:

(6570 + 2190): 3 = 2920 (cây)

Đáp số:....

Nửa chu vi HCN ban đầu :

\(200:2=100\left(m\right)\)

Hiệu của chiều dài và chiều rộng ban đầu :

\(\left(175+25\right):5=40\left(m\right)\)

Chiều dài ban đầu :

\(\left(100+40\right):2=70\left(m\right)\)

Chiều rộng ban đầu :

\(100-70=30\left(m\right)\)

Diện tích HCN ban đầu :

\(70x30=2100\left(m^2\right)\)

Hôm nay olm.vn sẽ hướng dẫn các em giải dạng toán nâng cao hai tỉ số hiệu không đổi cấu trúc đề thi hsg, thi chuyên em nhé.

 Bước 1: Lập luận chỉ ra đại lượng không đổi

 Bước 2: Tìm xem số thứ nhất lúc đầu bằng bao nhiêu phần của hiệu

 Bước 3 : Tìm xem số thứ nhất lúc sau bằng bao nhiêu phần của hiệu

 Bước 4 tìm hiệu rồi thay vào bước 1 để tìm số thứ nhất, cuối cùng tìm được số thứ hai

                                            Giải: 

Vì mỗi bạn cùng bớt đi 8 viên nên hiệu số bi của hai bạn không đổi so với lúc đầu.

Số bi của A lúc đầu  bằng:

7:(12 - 7) = \(\dfrac{7}{5}\) (hiệu số bi của bạn B và bạn A )

Số bi của A lúc sau bằng:

17: ( 32 - 17) = \(\dfrac{17}{15}\) (hiệu số bi của bạn B và bạn A)

8 viên bi ứng với phân số là: 

\(\dfrac{7}{5}\) - \(\dfrac{17}{15}\) = \(\dfrac{4}{15}\) (hiệu số bi của bạn B và bạn A)

Hiệu số bi của bạn B và bạn A là:  8 : \(\dfrac{4}{15}\) = 30 (viên bi)

Số bi của bạn A là: 30 \(\times\) \(\dfrac{7}{5}\) = 42 (viên bi)

Số bi của B là: 42 + 30 = 72 (viên bi)

Đáp số: Số bi của bạn A là: 42 viên, bạn B là 72 viên.

Thử lại ta có: Tỉ số bi của A lúc đầu và B lúc đầu là: 42 : 72 = \(\dfrac{7}{12}\) (ok)

    Tỉ số bi của B lúc sau và A lúc sau là: (72 - 8): (42 - 8) = \(\dfrac{32}{17}\) (ok)

Số bi của Cường là:

( 28 + 35 - 5 ) : 2 - 5 = 24 ( viên )

Đáp số: 24 viên 

chúc bn học giỏi nha:)))

Vì \(\overline{abcd}\) vào thế kỷ XI nên \(\overline{abcd}=10\overline{cd}\)

mà \(\overline{abcd}\) chia hết cho 2,5

⇒ \(\overline{abcd}=10\overline{c}0\)

mà \(\overline{abcd}\) chia hết cho 101

⇒ \(\overline{abcd}=1010\)

Vậy Lý Thái Tổ dời đô vào năm 1010

\(125.5^2.\dfrac{1}{625}.5^3=5^3.5^2.\dfrac{1}{5^4}.5^3=5^{3+2-4+3}=5^4\\ 8.32.\left(2^4.\dfrac{1}{32}\right)=2^3.2^5.2^4.\dfrac{1}{2^5}=2^{3+5+4-5}=2^7\\ 6^3.5^2.\left(\dfrac{5}{6}\right)^3=6^3.5^2.5^3:6^3=5^{2+3}.6^{3-3}=5^5.6^0=5^5.1=5^5\\ Bài.5A\)

\(Bài.5B\\ a,2401.\left(\dfrac{1}{7}\right)^2.\dfrac{1}{7}.49^2=7^4.\left(\dfrac{1}{7}\right)^3.\left(7^2\right)^2=7^4.\dfrac{1}{7^3}.7^4=7^{4-3+4}=7^5\\ b,9.81:\left(3^5.\dfrac{1}{27}\right)=3^2.3^4:\left(3^5.\dfrac{1}{3^3}\right)=3^{2+4}:\left(3^{5-3}\right)=3^6:3^2=3^{6-2}=3^4\\ c,3^4.7^2.\left(\dfrac{7}{3}\right)^4=3^4.7^2.7^4:3^4=\left(3^4:3^4\right).\left(7^2.7^4\right)=1.7^6=7^6\)

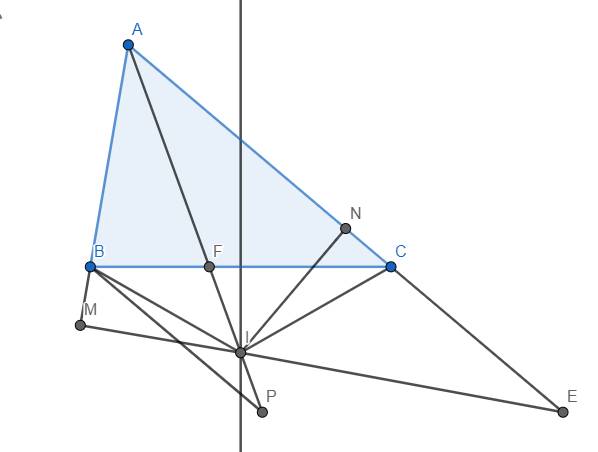
a) Do I nằm trên trung trực của đoạn BC nên \(IB=IC\). 

 Xét 2 tam giác IAM vuông tại M và IAN vuông tại N, ta có:

 AI là cạnh chung và \(\widehat{MAI}=\widehat{NAI}\) (do AI là phân giác góc BAC)

\(\Rightarrow\Delta IAM=\Delta IAN\left(ch-gn\right)\) \(\Rightarrow IM=IN\).

Lại xét 2 tam giác IMB vuông tại M và INC vuông tại N, có:

\(IB=IC\left(cmt\right);IM=IN\left(cmt\right)\)

\(\Rightarrow\Delta IMB=\Delta INC\left(ch-cgv\right)\) \(\Rightarrow MB=NC\left(đpcm\right)\)

b) Ta đã có \(IN\perp AE\) tại N nên ta chỉ cần chứng minh N là trung điểm của đoạn AE là xong. Thật vậy, ta có \(MB=NC\left(cmt\right)\) và \(AB=EC\left(gt\right)\) nên suy ra \(AB+MB=NC+EC\) hay \(AM=NE\).

Mặt khác, do \(\Delta IAM=\Delta IAN\left(cmt\right)\Rightarrow AM=AN\)

Từ đó suy ra \(AN=NE\) hay N là trung điểm AE. Ta có đpcm.

c) Qua B kẻ đường thẳng song song với AC cắt AI tại P. Khi đó ta có \(\widehat{BAP}=\widehat{CAP}=\widehat{BPA}\) nên tam giác ABP cân tại B, suy ra \(AB=BP\). Mặt khác, theo định lý Thales, ta có \(\dfrac{FB}{FC}=\dfrac{BP}{AC}=\dfrac{AB}{AC}< 1\) (do \(AB< AC\)) nên suy ra \(\dfrac{FB}{FC}< 1\) hay \(FB< FC\) (đpcm)

giúp t với 

\(A=2^{100}-2^{99}+2^{98}-2^{97}+....-2^3+2^2-2+1\\ A=\left(2^{100}+2^{98}+...+2\right)-\left(2^{99}+2^{97}+...+1\right)\)

Gọi \(\left(2^{100}+2^{98}+...+2\right)\)là B

\(B=\left(2^{100}+2^{98}+...+2\right)\\ 2B=2^{102}+2^{100}+.....+2^2\\ 2B-B=\left(2^{102}+2^{100}+.....+2^2\right)-\left(2^{100}+2^{98}+...+2\right)\\ B=2^{102}-2\)

Gọi \(\left(2^{99}+2^{97}+...+1\right)\) là C

\(C=\left(2^{99}+2^{97}+...+1\right)\\ 2C=2^{101}+2^{99}+....+2\\ 2C-C=\left(2^{101}+2^{99}+9^{97}+...+2\right)-\left(2^{99}+9^{97}+...+1\right)\\ C=2^{101}-1\)

\(A=B+C\\ =>A=2^{102}-2+2^{101}-1\\ A=2^{101}\left(2+1\right)-3\\ A=2^{101}\cdot3-3\\ A=3\cdot\left(2^{101}-1\right)\)

\(\dfrac{1}{2}A=2^{99}-2^{98}+...-1+\dfrac{1}{2}\\ \Rightarrow A-\dfrac{1}{2}A=2^{100}-\dfrac{1}{2}\\ \Rightarrow A=2^{101}-1\)

\(x< 100\Leftrightarrow x\le99\Leftrightarrow x-2\le97\)

 Ta thấy \(\left(x-2\right)⋮5,\left(x-2\right)⋮14\) mà \(\left(5,14\right)=1\) nên \(\left(x-2\right)⋮14.5=70\). Mà \(x-2\le97\) nên \(\left(x-2\right)\in\left\{0;70\right\}\) \(\Leftrightarrow x\in\left\{2;72\right\}\) . 

 Vậy \(x=2\) và \(x=72\) là các số thỏa ycbt.