\(B=\frac{2019}{1}+\frac{2018}{2}+\frac{2017}{3}+......+\frac{1}{2019}\)

\(=\left(\frac{2018}{2}+1\right)+\left(\frac{2017}{3}+1\right)+.....+\left(\frac{1}{2019}+1\right)+1\)

\(=\frac{2020}{2}+\frac{2020}{3}+\frac{2020}{4}+.....+\frac{2020}{2019}+\frac{2020}{2020}\)

\(=2020\left(\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+......+\frac{1}{2020}\right)\)

\(=2020A\)

\(\Rightarrow\frac{A}{B}=\frac{A}{2020A}=\frac{1}{2020}\)

10A=10¹¹-10/10¹¹-1

       =10¹¹-1-9/10¹¹-1

      =1 -  9/10¹¹-1

10B=10¹⁰-10/10¹⁰-1

      =10¹⁰-1-9/10¹⁰-1

      =1 -  9/10¹⁰-1

Vì 9/10¹¹-1<9/10¹⁰-1 nên 1 -  9/10¹¹-1>1 -  9/10¹⁰-1

hay 10A>10B

=>A>B(vì 10>0)

\(A=\frac{10^{10}-1}{10^{11}-1}\)

Nhân cả hai vế của A với 10 ta có

\(10A=\frac{10\times\left(10^{10}-1\right)}{10^{11}-1}\)

\(10A=\frac{10^{11}-10}{10^{11}-1}\)

\(10A=\frac{10^{11}-1+9}{10^{11}-1}\)

\(10A=\frac{10^{11}-1}{10^{11}-1}+\frac{9}{10^{11}-1}=1+\frac{9}{10^{11}-1}\left(1\right)\)

\(B=\frac{10^9-1}{10^{10}-1}\)

Nhân cả hai vế của B với 10 ta có 

\(10B=\frac{10\times\left(10^9-1\right)}{10^{10}-1}\)

\(10B=\frac{10^{10}-10}{10^{10}-1}\)

\(10B=\frac{10^{10}-1+9}{10^{10}-1}\)

\(10B=\frac{10^{10}-1}{10^{10}-1}+\frac{9}{10^{10}-1}=1+\frac{9}{10^{10}-1}\left(2\right)\)

\(Từ\left(1\right)và\left(2\right)\Rightarrow1+\frac{9}{10^{11}-1}< 1+\frac{9}{10^{10}-1}\)

                          \(\Rightarrow10A< 10B\)

                           Vậy A < B

Ròng rọc là một bánh xe có rãnh có thê quay quanh một trục. Căn cứ vào cách sử dụng ròng rọc mà người ta có thể phân ròng rọc làm hai loại (ròng rọc cố định và ròng rọc động).

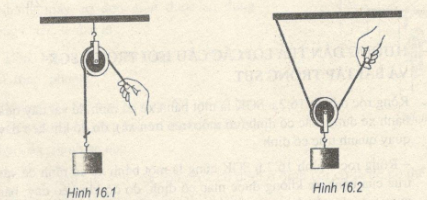
Khi nâng những vật nặng lên cao người ta có thể treo ròng rọc lên cao vắt dây qua rãnh của ròng rọc, buộc vật vào một đầu dây, muốn kéo vật lên thì phải kéo đầu dây kia xuống làm bánh xe quay tại chỗ. Ròng rọc được sử dụns theo cách này được gọi là ròng rọc cố định 

Khi nâng những vật nặng lên cao người ta có thể buộc cố định một đầu dây lên cao, luồn dây qua rãnh của ròng rọc, móc vật vào ròng rọc. Muốn kéo vật lên, thì phải kéo đầu dây kia lên làm bánh xe vừa quay, vừa chuyển động lên cùng vật. Ròng rọc được sử dụng theo cách này được gọi là ròng rọc động

175 km = 175 000 000 mm

Quãng đường sắt từ ga Hà Nội đến Thanh Hóa:

175 000 000 : 2 500 000 = 70 (mm)

Đáp số :...

3x+4xy-3x+9xy-5xz+9-xz-1=13xy-6xz+8

Chúc hok tốt

3x+4xy-3x+9xy-5xz=9-xz-1

=(3x-3x)+(4xy+9xy)-(5xz+xz)+(9-1)

=13xy-6xz+8