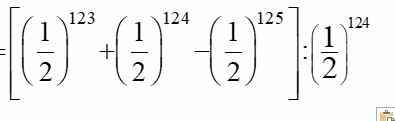cho P(x) là 1 đa thức bậc 4 có hệ số cao nhất là 1 thoả mãn P(1)=3;P(3)=11;P(5)=27.Tính P(-2)+7P(6)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Tổng số phần bằng nhau là : 7 + 3 = 10 ( phần )
Chiều dài HCN là : 60 : 10 x 7 = 42 ( m )
Chiều rộng HCN là : 60 - 42 = 18 ( m )
b) Diện tích HCN là : 42 x 18 = 756 ( m2 )
Đáp số : a) 42m ; 18m
b) 756m2
a, Nửa chu vi hình chữ nhật là: 60 : 2 = 30
Gọi chiều dài và chiều rộng hình chữ nhật lần lượt là \(x\); y (m) \(x;y>0\)
Theo bài ra ta có: \(\dfrac{x}{y}\) = \(\dfrac{7}{3}\) ⇒ \(\dfrac{x}{7}=\dfrac{y}{3}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{7}\) = \(\dfrac{y}{3}\) = \(\dfrac{x+y}{7+3}\) = \(\dfrac{30}{10}\) = 3
\(x\) = 3\(\times\) 7 = 21
y = 3 x 3 = 9
Chiều dài hình chữ nhật là: 21 m
Chiều rộng hình chữ nhật là 9 m
b, Diện tích hình chữ nhật là: 21 x 9 = 189 (m2)
Kết luận: diện tích hình chữ nhật là 189 m2

đây nha bạn
Thành phố nơi em sinh sống là một khu đô thị vốn dĩ ồn ào, hối hả, nhưng mỗi buổi sáng sớm tinh mơ, thành phố em mới thanh bình làm sao! Buổi sáng hôm ấy, em thức dậy từ rất sớm để tập thể dục và đi học. Không gian yên tĩnh tới lạ thường làm sao! Không có tiếng còi xe, không có tiếng người qua lại, ... Cả không gian yên tĩnh tới mức em có thể nghe từ xa tiếng giỏ thổi lao xao qua các tán cây, tiếng một vài chú chim dậy sớm hót líu lo. Con đường vốn đông đúc người qua lại mà giờ đây thật yên tĩnh và bình lặng. Bên các vỉa hè chỉ có một vài quán ăn nhỏ, bình dân đã mở cửa để chuẩn bị cho một ngày mai. Đó quả thực sự là một không gian yên tĩnh vô cùng. Thành phố em khi ấy thật thanh bình biết bao nhiêu.

Lời giải:
a.
$(\frac{-1}{3})^3.x=\frac{1}{81}=(\frac{-1}{3})^4$
$\Rightarrow x=(\frac{-1}{3})^4: (\frac{-1}{3})^3=\frac{-1}{3}$
b.
$2^2.16> 2^x> 4^2$
$\Rightarrow 2^2.2^4> 2^x> (2^2)^2$
$\Rightarrow 2^6> 2^x> 2^4$
$\Rightarrow 6> x> 4$
$\Rightarrow x=5$ (với điều kiện $x$ là số tự nhiên nhé)
c.
$9.27< 3^x< 243$
$3.3^3< 3^x< 3^5$
$\Rightarrow 3^4< 3^x< 3^5$
$\Rightarrow 4< x< 5$
Với $x$ là stn thì không có số nào thỏa mãn.


Lời giải:
$2^{299}< 2^{300}=(2^3)^{100}=8^{100}$
$3^{201}> 3^{200}=(3^2)^{100}=9^{100}$
$\Rightarrow 3^{201}> 9^{100}> 8^{100}> 2^{299}$

B = \(\left[\left(\dfrac{1}{2}\right)^{123}+\left(\dfrac{1}{2}\right)^{124}-\left(\dfrac{1}{2}\right)^{125}\right]\): \(\left(\dfrac{1}{2}\right)\)124
B = \(\left(\dfrac{1}{2}\right)\)123.\(\left(1+\dfrac{1}{2}-\dfrac{1}{4}\right)\): (\(\dfrac{1}{2}\))124
B = (\(\dfrac{1}{2}\))123. \(\dfrac{5}{4}\): (\(\dfrac{1}{2}\))124
B = (\(\dfrac{1}{2}\))124. \(\dfrac{5}{2}\) : (\(\dfrac{1}{2}\))124
B = \(\dfrac{5}{2}\)
Lời giải:
Đặt phép tính trên là $A$
$A=(\frac{1}{2})^{123}\left[1+(\frac{1}{2})-(\frac{1}{2})^2\right]: (\frac{1}{2})^{124}$
$=\left[1+\frac{1}{2}-(\frac{1}{2})^2\right]: \frac{1}{2}=\frac{5}{4}.2=\frac{5}{2}$

Lời giải:
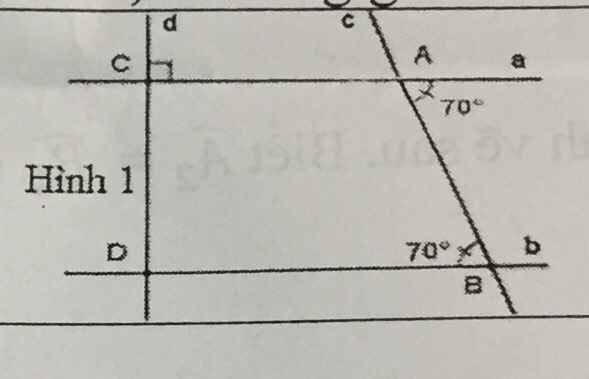
a.
Ta thấy $\widehat{aAb}=\widehat{ABD}=70^0$. Mà 2 góc này ở vị trí so le trong nên $a\parallel b$
b.
$\widehat{CAc}=\widehat{aAb}=70^0$ (2 góc đối đỉnh)
Vì $a\parallel b, a\perp d\Rightarrow b\perp d$
$\Rightarrow \widehat{CDB}=90^0$