354dm3 + 330000cm3 x 2 = ???
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


d.
\(\dfrac{2^3.5^4.49}{35.2^2.175}=\dfrac{2^3.5^4.7^2}{5.7.2^2.7.5^2}=\dfrac{2^3.5^4.7^2}{2^2.5^3.7^2}=2.5=10\)
\(\dfrac{12.2^a}{3^2.8^b}=\dfrac{3.2^2.2^a}{3^2.\left(2^3\right)^b}=\dfrac{3.2^{a+2}}{3^2.2^{3b}}=\dfrac{2^{a-3b+2}}{3}\)

Đổi : \(9dm=0,9m\)
Diện tích xung quanh của thùng là:
\(\left(1,2+0,8\right)\times2\times0,9=3,6\) ( m2 )
Diện tích mặt đáy thùng đó là:
\(1,2\times0,8=0,96\) ( m2 )
Diện tích tôn để làm thùng là:
\(3,6+0,96=4,56\) ( m2 )
Đ/S:....

\(\dfrac{2.4+2.4.8+4.8.16+8.16.32}{3.4+2.6.8+4.12.16+8.24.32}\)
\(=\dfrac{1.2.4+2.1.2.2.2.4+4.1.4.2.4.4+8.1.8.2.8.4}{3.4+2.1.2.3.2.4+4.1.4.3.4.4+8.1.8.3.8.4}\)
\(=\dfrac{1.2.4+2^3.1.2.4+4^3.1.2.4+8^3.1.2.4}{1.3.4+2^3.1.3.4+4^3.1.3.4+8^3.1.3.4}\)
\(=\dfrac{1.2.4.\left(1+2^3+4^3+8^3\right)}{1.3.4.\left(1+2^3+4^3+8^3\right)}\)
\(=\dfrac{2}{3}\)

Góc IA = góc IE làm sao được em. Góc thì phải có 3 đỉnh chứ sao mỗi góc ở đây có hai đỉnh vậy em

Đổi 1m 2dm = 12dm
Độ dài cạnh hình vuông là
\(12\div4=3\)(dm)
Đáp số 3 dm

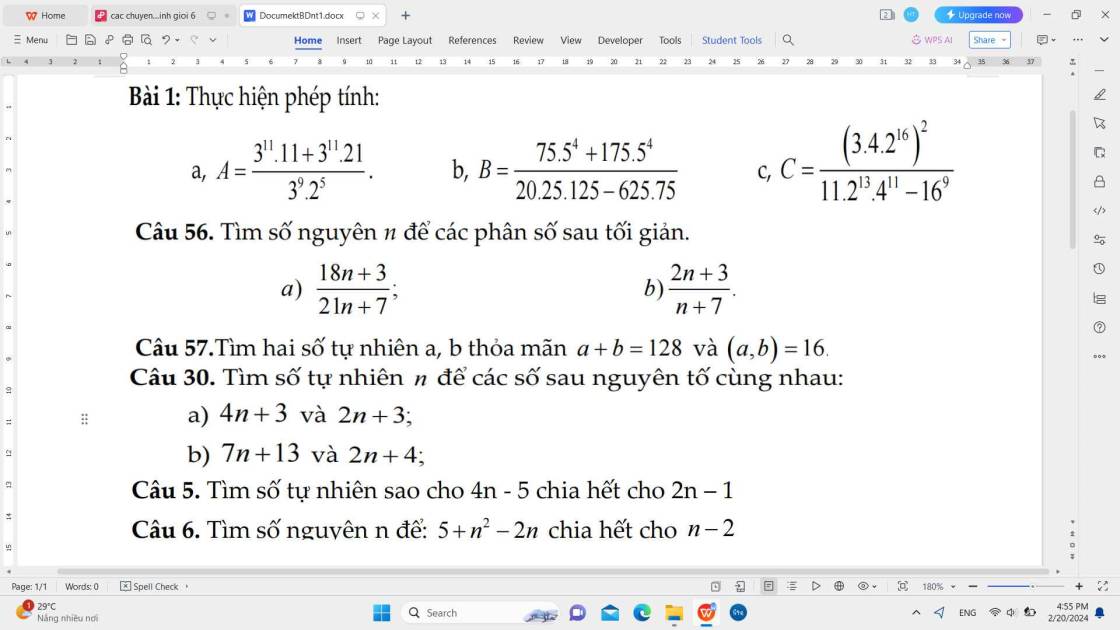
Do \(\left(a,b\right)=16\), đặt \(\left\{{}\begin{matrix}a=16x\\b=16y\end{matrix}\right.\) với \(\left(x,y\right)=1\)
\(a+b=128\Rightarrow16x+16y=128\)
\(\Rightarrow x+y=8\)
Mà \(\left(x,y\right)=1\Rightarrow\left(x;y\right)=\left(1;7\right);\left(7;1\right);\left(3;5\right);\left(5;3\right)\)
\(\Rightarrow\left(a;b\right)=\left(16;112\right);\left(112;16\right);\left(48;80\right);\left(80;48\right)\) có 4 cặp thỏa mãn

1 ngày thì dùng hết số ki-lô-gam gạo là:
754 : 13 = 58 (kg)
30 ngày thì dùng hết số ki-lô-gam gạo là:
58 x 30 = 1740 (kg)
Đ/S: 1740 kg gạo

Ta có: \(D\left(x\right)=2x^2+3y^2+4z^2-2\left(x+y+z\right)+2\)
\(=2x^2+3y^2+4z^2-2x-2y-2z+2\)
\(=\left(2x^2-2x\right)+\left(3y^2-2y\right)+\left(4z^2-2z\right)+2\)
\(=2\left(x^2-x\right)+3\left(y^2-\dfrac{2}{3}y\right)+4\left(z^2-\dfrac{1}{2}z\right)+2\)
\(=2\left[x^2-2\cdot x\cdot\dfrac{1}{2}+\left(\dfrac{1}{2}\right)^2-\left(\dfrac{1}{2}\right)^2\right]+3\left[y^2-2\cdot y\cdot\dfrac{1}{3}+\left(\dfrac{1}{3}\right)^2-\left(\dfrac{1}{3}\right)^2\right]+4\left[z^2-2\cdot z\cdot\dfrac{1}{4}+\left(\dfrac{1}{4}\right)^2-\left(\dfrac{1}{4}\right)^2\right]+2\)\(=2\left(x-\dfrac{1}{2}\right)^2-\dfrac{1}{2}+3\left(y-\dfrac{1}{3}\right)^2-\dfrac{1}{3}+4\left(z-\dfrac{1}{4}\right)^2-\dfrac{1}{4}+2\)
\(=2\left(x-\dfrac{1}{2}\right)^2+3\left(y-\dfrac{1}{3}\right)^2+4\left(z-\dfrac{1}{4}\right)^2+\dfrac{11}{12}\)
Mà: \(\left\{{}\begin{matrix}2\left(x-\dfrac{1}{2}\right)^2\ge0\forall x\\3\left(y-\dfrac{1}{3}\right)^2\ge0\forall y\\4\left(y-\dfrac{1}{4}\right)^2\ge0\forall z\end{matrix}\right.\)
\(\Rightarrow D\left(x\right)=2\left(x-\dfrac{1}{2}\right)^2+3\left(y-\dfrac{1}{3}\right)^2+4\left(z-\dfrac{1}{4}\right)^2+\dfrac{11}{12}\ge\dfrac{11}{12}\forall x,y,z\)
Dấu "=" xảy ra khi:
\(\left\{{}\begin{matrix}x-\dfrac{1}{2}=0\\y-\dfrac{1}{3}=0\\z-\dfrac{1}{4}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=\dfrac{1}{3}\\z=\dfrac{1}{4}\end{matrix}\right.\)
Vậy: ...
D(x)=2(x2−x)+(3y2−2y)+(4z2−2z)+2
=2(�2−�+14)+3(�2−23�+19)+[(2�)2−2�+14]+2−12−13−14=2(x2−x+41)+3(y2−32y+91)+[(2z)2−2z+41]+2−21−31−41
=2(�−12)2+3(�−13)2+(2�−12)2+112≥112=2(x−21)2+3(y−31)2+(2z−21)2+211≥211
Vậy giá trị nhỏ nhất của �D là: 112211 tại (�,�,�)=(12;13;14)(x,y,z)=(21;31;41).

a: Gọi I là trung điểm của MC
=>\(MI=IC=\dfrac{MC}{2}\)
mà \(AM=\dfrac{MC}{2}\)
nên AM=MI=IC
Vì AM=MI nên M là trung điểm của AI
Xét ΔBMC có
D,I lần lượt là trung điểm của CB,CM
=>DI là đường trung bình của ΔBMC
=>DI//BM và \(DI=\dfrac{BM}{2}\)
DI//BM nên OM//DI
Xét ΔADI có
M là trung điểm của AI
MO//DI
Do đó: O là trung điểm của AD
b: Xét ΔADI có
O,M lần lượt là trung điểm của AD,AI
=>OM là đường trung bình của ΔADI
=>\(OM=\dfrac{1}{2}DI=\dfrac{1}{2}\cdot\dfrac{1}{2}\cdot BM=\dfrac{1}{4}BM\)
a: Gọi I là trung điểm của MC
=>��=��=��2MI=IC=MC:2
mà ��=��2AM=MC:2
=> AM=MI=IC
Vì AM=MI => M là trung điểm của AI
Xét ΔBMC có:
D,I lần lượt là trung điểm của CB,CM
=>DI là đường trung bình của ΔBMC
=>DI//BM , ��=��2DI=BM:2
DI//BM => OM//DI
Xét ΔADI có:
M là trung điểm của AI
MO//DI
=> O là trung điểm của AD
b) Xét ΔADI có
O,M lần lượt là trung điểm của AD,AI
=>OM là đường trung bình của ΔADI
=>��=12��=12⋅12⋅��=14��OM=
DI:2=BM:4(đpcm)
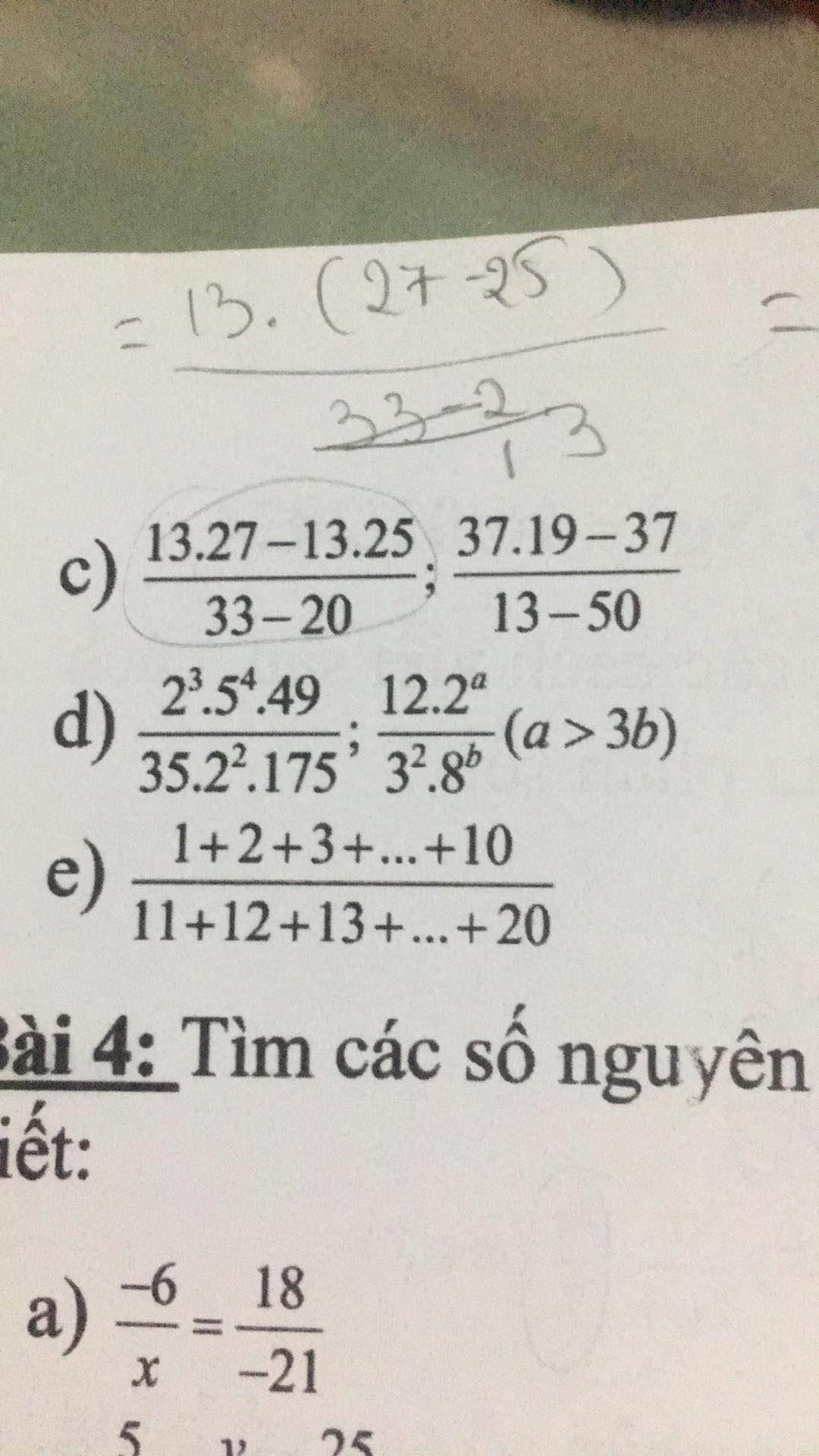
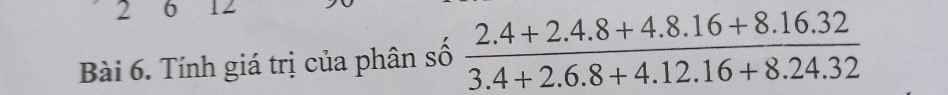
=354dm3+330dm3×2
=354dm3+660dm3
=1014dm3
354 dm3 + 330 000 cm3 x 2
= 354 dm3 + 660 000 cm3
= 354 dm3 + 660 dm3
= 1014 dm3