cho tam giac vuong abc co duong thang d cat ab ac tai d, e goi lan luot i,j,k,h la trung diem de,be,bc,dc chung minh ijkh la hinh chu nhat
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
31 tháng 10 2019
\(10.3^x=81\)
\(3^x=80:10\)
\(3^x=8\)
\(\Rightarrow3^x=\varnothing\)
\(20-\left(x-1\right)^3=\frac{1}{16}\)
\(\left(x-1\right)^3=20-\frac{1}{16}\)
\(\left(x-1\right)^3=\frac{320}{16}-\frac{1}{16}\)
\(\left(x-1\right)^3=\frac{319}{16}\)
\(\Rightarrow\left(x-1\right)^3=\varnothing\Leftrightarrow x=\varnothing\)
VA
2
C
31 tháng 10 2019
\(2-\left(\frac{-3}{2}\right)^0+\frac{16}{4}:\frac{1}{2}\)
\(=2-1+4:\frac{1}{2}\)
\(=1+8=9\)
HH
31 tháng 10 2019
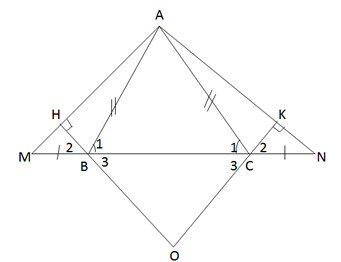
a) ∆ABC cân, suy ra ˆB1=ˆC1B1^=C1^
⇒ˆABM=ˆACN⇒ABM^=ACN^
∆ABM và ∆CAN có:
AB = AC (gt)
ˆABM=ˆACNABM^=ACN^
BM = ON (gt)
Suy ra ˆM=ˆNM^=N^
=>∆AMN là tam giác cân ở A.
b) Hai tam giác vuông ∆BHM và ∆CKN có :
BM = CN (gt)
ˆM=ˆNM^=N^ (CM từ câu a)
Nên ∆BHM = ∆CHN (cạnh huyền, góc nhọn)
Suy ra BH = CK.
c) Theo câu (a) ta có tam giác AMN cân ở A nên AM = AN (*)
Theo câu b ta có ∆BHM = ∆CKN nên suy ra HM = KN (**).
Do đó AH = AM – HM = AN – KN (theo (*) và (**)) = AK
Vậy AH = AK.
d) ∆BHM = ∆CKN suy ra ˆB2=ˆC2B2^=C2^
Mà ˆB2=ˆB3;ˆC2=ˆC3B2^=B3^;C2^=C3^ (đối đỉnh)
Nên ˆB3=ˆC3B3^=C3^ .
Vậy ∆OBC là tam giác cân.
e) Khi ˆBAC=600BAC^=600 và BM = CN = BC.
+Tam giác cân ABC có ˆBAC=600BAC^=600 nên là tam giác đều.
Do đó: AB = BC = AC = BM = CN
ˆABM=ˆACN=1200ABM^=ACN^=1200 (cùng bù với 600)
∆ABM cân ở B nên ˆM=ˆBAM=1800–12002=300M^=BAM^=1800–12002=300 .
Suy ra ˆANM=ˆAMN=300ANM^=AMN^=300 .
Và ˆMAN=1800–(ˆAMN+ˆANM)=1800–2.300=1200MAN^=1800–(AMN^+ANM^)=1800–2.300=1200
Vậy ∆AMN có ˆM=ˆN=300;ˆA=1200.M^=N^=300;A^=1200.
+∆BHM có: ˆM=300M^=300 nên ˆB2=600B2^=600 (hai góc phụ nhau)
Suy ra ˆB3=600B3^=600
Tương tự ˆC3=600C3^=600
Tam giác OBC có ˆB3=ˆC3=600B3^=C3^=600 nên tam giác OBC là tam giác đều.
(Tam giác cân có một góc bằng 600 nên là tam giác đều).
DT
2
31 tháng 10 2019
b)
(x-7)x+1 - (x-7)x+11 = 0
=>(x-7)x+1.[1-(x-7)10]=0
=>(x-7)x+1=0 hoặc 1-(x-7)10=0
=>x-7=0 hoặc (x-7)10=1
=>x=7 hoặc x-7=1 hoặc x-7=-1
=>x=7 hoặc x=8 hoặc x=6
31 tháng 10 2019
a)
(x-1)x+2=(x-1)x+6
(x-1)x+2-(x-1)x+6=0
(x-1)x+2 . [1-(x-1)4]=0
=> (x-1)x+2=0 hoặc 1-(x-1)4=0
=>x-1=0 =>(x-1)4=1
=>x=1 =>x-1=1 hoặc x-1=-1
=> x=2 hoặc x=0
vậy x \(\in\) {0;1;2}
NC
4
VC
Vũ Cao Minh
CTV
VIP
31 tháng 10 2019
Vì \(3x=8y\Rightarrow\frac{x}{8}=\frac{y}{3}\Rightarrow\frac{x}{8}=\frac{2y}{6}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có : \(\frac{x}{8}=\frac{2y}{6}=\frac{x-2y}{8-6}=\frac{4}{2}=2\)
\(\Rightarrow x=2.8=16\) Thử lại : \(3x=16\times3=48\)
\(\Rightarrow y=2.6\div2=6\) \(8y=6\times8=48\)
Vậy \(x=16;y=6\)
31 tháng 10 2019
Vì \(3x=2y\)nên:
\(\Rightarrow\frac{x}{2}=\frac{y}{3}\)
Ta thấy: \(\frac{y}{3}=\frac{2y}{6}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{x}{2}=\frac{y}{3}=\frac{2y}{6}=\frac{x-2y}{6-4}=\frac{4}{2}=2\)
\(\Rightarrow x=2.2=4\)
\(\Rightarrow y=2.3=6\)
31 tháng 10 2019
a) 3,5(15) = 3,5 + 0,0(15) = 3,5 + 1,5. 0,(01) = 3,5 + 1,5.1/99 = 3,5 + 1/66 = 116/33
b) Ta có: \(\frac{2x-y}{x+y}=\frac{2}{3}\)
=> (2x - y).3 = 2(x + y)
=> 6x - 3y = 2x + 2y
=> 6x - 2x = 2y + 3y
=> 4x = 5y
=> \(\frac{x}{y}=\frac{5}{4}\)
c) Đặt : \(\frac{a}{b}=\frac{c}{d}=k\) => \(\hept{\begin{cases}a=bk\\c=dk\end{cases}}\)
Khi đó, ta có:
\(\frac{\left(bk\right)^2+bk.dk}{\left(dk\right)^2+dk.bk}=\frac{b^2k^2+bdk^2}{d^2k^2+bdk^2}=\frac{k^2\left(b^2+bd\right)}{k^2\left(d^2+bd\right)}=\frac{b^2+bd}{d^2+bd}\)
=> Đpcm
31 tháng 10 2019
Có:\(\frac{x}{5}=\frac{y}{6}\Rightarrow\frac{x}{20}=\frac{y}{24}\)
\(\frac{y}{8}=\frac{z}{11}\Rightarrow\frac{y}{24}=\frac{z}{33}\)
\(\Rightarrow\frac{x}{20}=\frac{y}{24}=\frac{z}{33}\)
Áp dụng t/c dãy tỉ số bằng nhau ,có:
\(\frac{x}{20}=\frac{y}{24}=\frac{z}{33}=\frac{x+y-z}{20+24-33}=\frac{44}{11}=4\)
\(\Rightarrow\hept{\begin{cases}x=4.20=80\\y=4.24=96\\z=4.33=132\end{cases}}\)
Vậy.............................