Câu 6. (2,0 điểm) Cho ABC vuông tại A (AB < AC) có đường cao AH. a) Chứng minh ABC HBA và = . b) Trên cạnh BC lấy điểm D sao cho BD = BA. Qua D, vẽ DE AC tại E (E thuộc AC). Chứng minh = và AH.DC = DH.AC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ĐKXĐ: x<>-2
\(x^2+\dfrac{4x^2}{\left(x+2\right)^2}=5\)
=>\(\dfrac{\left(x^2+2x\right)^2+4x^2}{\left(x+2\right)^2}=5\)
=>\(x^4+4x^3+4x^2+4x^2=5\left(x^2+4x+4\right)\)
=>\(x^4+4x^3+8x^2-5x^2-20x-20=0\)
=>\(x^4+4x^3+3x^2-20x-20=0\)
=>\(\left(x-2\right)\left(x+1\right)\left(x^2+5x+10\right)=0\)
mà \(x^2+5x+10>0\forall x\)
nên (x-2)(x+1)=0
=>\(\left[{}\begin{matrix}x=2\left(nhận\right)\\x=-1\left(nhận\right)\end{matrix}\right.\)

a: Xét ΔMBA vuông tại M và ΔABC vuông tại A có
\(\widehat{MBA}\) chung
Do đó: ΔMBA~ΔABC
b: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
ΔMBA~ΔABC
=>\(\dfrac{MA}{AC}=\dfrac{BA}{BC}\)
=>\(MA=\dfrac{AB\cdot AC}{BC}=\dfrac{6\cdot8}{10}=4,8\left(cm\right)\)
Xét ΔBMA có BN là phân giác
nên \(\dfrac{NA}{NM}=\dfrac{BA}{BM}\left(1\right)\)
Xét ΔBAC có BG là phân gíac
nên \(\dfrac{GC}{GA}=\dfrac{BC}{BA}\left(2\right)\)
ΔMBA~ΔABC
=>\(\dfrac{BA}{BM}=\dfrac{BC}{BA}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\dfrac{GC}{GA}=\dfrac{NA}{NM}\)
=>\(GC\cdot NM=NA\cdot GA\)

Truyền và biến đổi chuyển động là gì? Nêu một số cơ cấu truyền động phổ biến.


a.
Để (a) song song (b) \(\Leftrightarrow\left\{{}\begin{matrix}2m=1\\-1\ne2\end{matrix}\right.\)
\(\Rightarrow m=\dfrac{1}{2}\)
b.
Gọi A là giao điểm của (C) với trục hoành
\(\Rightarrow x_A-2=0\Rightarrow x_A=2\)
\(\Rightarrow A\left(2;0\right)\)
Để (a) cắt (c) tại 1 điểm thuộc trục hoành \(\Rightarrow\) (a) đi qua A
Thay tọa độ A vào pt (a) ta được:
\(2m.2-1=0\)
\(\Rightarrow m=\dfrac{1}{4}\)

Gọi số tuổi của Nam hiện tại là x tuôi (với 0<x<62)
Do tuổi của Nam và ba cộng lại là 62 nên tuổi của ba hiện tại là: \(62-x\) tuổi
Tuổi của Nam 7 năm nữa là: \(x+7\)
Tuổi của ba Nam 7 năm sau nữa là: \(62-x+7=69-x\)
Do 7 năm sau tuổi của ba gấp 3 lần tuổi Nam nên ta có pt:
\(69-x=3\left(x+7\right)\)
\(\Leftrightarrow69-x=3x+21\)
\(\Leftrightarrow4x=48\)
\(\Leftrightarrow x=12\)
Vậy năm nay Nam 12 tuổi
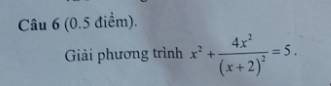


a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABC}\) chung
Do đó: ΔABC~ΔHBA
b: Ta có: \(\widehat{HAD}+\widehat{BDA}=90^0\)(ΔHAD vuông tại H)
\(\widehat{CAD}+\widehat{BAD}=\widehat{BAC}=90^0\)
mà \(\widehat{BDA}=\widehat{BAD}\)(ΔBAD cân tại B)
nên \(\widehat{HAD}=\widehat{CAD}\)
=>AD là phân giác của góc HAC
Xét ΔAHC có AD là phân giác
nên \(\dfrac{DH}{DC}=\dfrac{AH}{AC}\)
=>\(DH\cdot AC=AH\cdot DC\)