một vật sáng AB đặt trước thấu kính hội tụ một khoảng d = OA = 12 cm(A nằm trên trục chính của thấu kính ) và vuông góc với trục chính của thấu kính có tiêu cự F= 15 cm
a) hãy dựng ảnh , nêu đặc điểm của ảnh A'B' B) tính khoảng cách từ ảnh đến thấu kínhHãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) PTHH: \(CH_4+2O_2\underrightarrow{t^o}CO_2+2H_2O\)
\(C_2H_4+3O_2\underrightarrow{t^o}2CO_2+2H_2O\)
b) Đặt \(n_{CH_4}=x\left(mol\right);n_{C_2H_4}=y\left(mol\right)\). Khi đó \(22,4x+22,4y=4,48\) \(\Leftrightarrow x+y=0,2\)
Từ PTHH \(\Rightarrow n_{O_2\left(1\right)}=2x\left(mol\right)\)\(;n_{O_2\left(2\right)}=3y\left(mol\right)\). Khi đó \(2x.22,4+3y.22,4=11,2\) \(\Leftrightarrow2x+3y=0,5\)
Vậy ta có \(\left\{{}\begin{matrix}x+y=0,2\\2x+3y=0,5\end{matrix}\right.\Leftrightarrow x=y=0,1\left(mol\right)\)
\(\Rightarrow\%V_{CH_4}=\%V_{C_2H_4}=50\%\)

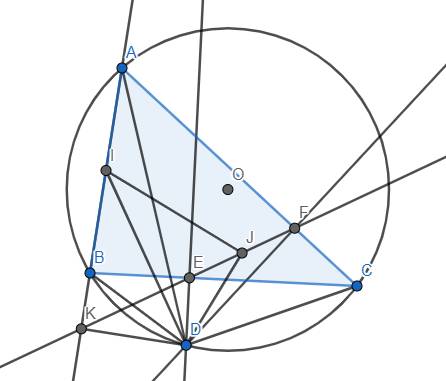
a) Theo đề bài, ta có \(\widehat{DEC}=\widehat{DFC}=90^o\) \(\Rightarrow\) Tứ giác CDEF nội tiếp do có 2 đỉnh kề nhau E, F cùng nhìn cạnh CD dưới góc vuông. \(\Rightarrow\widehat{DFE}=\widehat{DCE}=\widehat{DCB}=\widehat{DAB}\) (do tứ giác ABDC nội tiếp nên \(\widehat{DCB}=\widehat{DAB}\)). Từ đó suy ra đpcm.
b) Có \(\widehat{KBD}=\widehat{ACD}\) (do tứ giác ABDC nội tiếp) và \(\widehat{ACD}=\widehat{KED}\) (do tứ giác CDEF nội tiếp) \(\Rightarrow\widehat{KBD}=\widehat{KED}\) \(\Rightarrow\) Tứ giác DKBE nội tiếp.
Mặt khác, \(\widehat{BDA}=\widehat{BCA}=\widehat{EDF}\) và \(\widehat{BAD}=\widehat{BCD}=\widehat{EFD}\)
\(\Rightarrow\Delta DBA~\Delta DEF\left(g.g\right)\)\(\Rightarrow\dfrac{DA}{DF}=\dfrac{DB}{DE}\) \(\Rightarrow DA.DE=DB.DF\)
c) \(\Delta DBA~\Delta DEF\Rightarrow\dfrac{DB}{DE}=\dfrac{AB}{EF}=\dfrac{2BI}{2EJ}=\dfrac{BI}{EJ}\) . Lại có \(\widehat{DBI}=\widehat{DEJ}\) nên \(\Delta DBI~\Delta DEJ\left(c.g.c\right)\) \(\Rightarrow\widehat{DIB}=\widehat{DJE}\) hay \(\widehat{DIK}=\widehat{DJK}\) \(\Rightarrow\) Tứ giác DJIK nội tiếp \(\Rightarrow\) \(\widehat{DJI}=180^o-\widehat{DKI}\) . Lại có \(\widehat{DKI}=180^o-\widehat{BED}=90^o\) (do tứ giác DKBE nội tiếp) \(\Rightarrow\widehat{DJI}=90^o\) \(\Rightarrow\) đpcm

a. Để có một trận đấu ta có 5 cách chọn đội thứ nhất, 4 cách chọn đội thứ 2. Vì mỗi đội chỉ đấu với nhau 1 trận nên số trận đấu của bảng đấu là: 5 .4 : 2 = 10 trận.
b. Mỗi trận đấu tổng điểm của hai đội là 3 điểm hoặc 2 điểm
Tổng điểm tối đa của 5 đội là: 10 . 3 = 30 điểm
Tổng điểm thực tế của 5 là: 10 + 9 + 6 + 4 +0 =29 điểm
Điểm thực tế ít hơn điểm tối đa là 1 nên có 1 trận hòa.
Hai đội A và D hòa nhau, vì điểm 2 đội không chia hết cho 3.