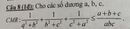Ta có: \(\frac{a}{b^3}+\frac{b}{c^3}+\frac{c}{d^3}+\frac{d}{a^3}\ge4\sqrt[4]{\frac{a}{b^3}\frac{b}{c^3}\frac{c}{d^3}\frac{d}{a^3}}=\frac{4}{\sqrt{abcd}}\)

\(\Rightarrow\left(\frac{a}{b^3}+\frac{b}{c^3}+\frac{c}{d^3}+\frac{d}{a^3}\right)\left(a+b\right)\left(c+d\right)\ge\frac{4}{\sqrt{abcd}}2\sqrt{ab}2\sqrt{cd}=16\)

Đẳng thức xảy ra <=> a=b=c=d

Theo định lý hàm cos

\(a^2=b^2+c^2-2bc.\cos A\Rightarrow\cos A=\frac{b^2+c^2-a^2}{2bc}\)

\(c^2=a^2+b^2-2ab.\cos C\Rightarrow\cos C=\frac{a^2+b^2-c^2}{2ab}\)

\(b^2=a^2+c^2-2ac.\cos B\Rightarrow\cos B=\frac{a^2+c^2-b^2}{2ac}\)

\(\Rightarrow a\left(c\cos C-b\cos B\right)=a\left(c.\frac{a^2+b^2-c^2}{2ab}-b.\frac{a^2+c^2-b^2}{2ac}\right)=\)

\(=\frac{c^2\left(a^2+b^2-c^2\right)-b^2\left(a^2+c^2-b^2\right)}{2bc}=\)

\(=\frac{a^2c^2+b^2c^2-c^4-a^2b^2-b^2c^2+b^4}{2bc}=\frac{\left(b^4-c^4\right)-a^2\left(b^2-c^2\right)}{2bc}=\)

\(=\frac{\left(b^2+c^2\right)\left(b^2-c^2\right)-a^2\left(b^2-c^2\right)}{2bc}=\frac{\left(b^2-c^2\right)\left(b^2+c^2-a^2\right)}{2bc}=\left(b^2-c^2\right)\cos A\left(dpcm\right)\)

Ta có VP= a(bcosC - ccosB)= a(\(b.(b^2+a^2-c^2)/2ab\) - c. (\(a^2+c^2-b^2\))/ 2ac))
                                             = ab. (\(b^2+a^2-c^2)/2ab-ac.(a^2+c^2-b^2)/2ac \)
                                             = (\(2b^2-2c^2)\)/2
                                             = \(b^2-c^2\) = VT
=> đpcm

A B C D E 5 3 4

áp dụng pitago đảo cho tam giác ABC ta thấy ABC vuông tại A . Kẻ DE vuông góc với AC. Xét tam giác ABC và EDC có 

\(\hept{\begin{cases}\widehat{BAC}=\widehat{DEC}=90^o\\BC=CD\\\widehat{BCA}=\widehat{DCE}\end{cases}}\)suy ra tam giác ABC=EDC suy ra \(\hept{\begin{cases}AC=EC=4\\AB=ED=3\end{cases}\Rightarrow\hept{\begin{cases}AE=8\\ED=3\end{cases}}}\)

ÁP DỤNG ĐỊNH LÍ PITAGO CHO TAM GIÁC VUÔNG ADE VUÔNG TẠI E TA CÓ \(AD=\sqrt{AE^2+ED^2}=\sqrt{73}\)