 Cứu tui bài natf
Cứu tui bài natf
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét đường tròn (O) có tiếp tuyến MB tại B nên
\(\widehat{MBI}=\dfrac{1}{2}sđ\stackrel\frown{IB}\)
Lại có \(\widehat{IBH}=90^o-\widehat{BIH}\)
\(=90^o-\widehat{OIB}\)
\(=90^o-\dfrac{180^o-\widehat{IOB}}{2}\)
\(=\dfrac{180^o-180^o+sđ\stackrel\frown{IB}}{2}\)
\(=\dfrac{1}{2}sđ\stackrel\frown{IB}\)
Do đó \(\widehat{MBI}=\widehat{IBH}\) hay BI là tia phân giác của \(\widehat{MBH}\)
\(\Rightarrow d\left(I,MB\right)=d\left(I,BH\right)=IH=R_I\)
Suy ra MB là tiếp tuyến của (I)

Bài 4:
\(a)x-7< 2-x\\ \Leftrightarrow x+x< 2+7\\ \Leftrightarrow2x< 9\\ \Leftrightarrow x< \dfrac{9}{2}\\ b)x+2\le2+3x\\ \Leftrightarrow3x-x\ge2-2=0\\ \Leftrightarrow2x\ge0\\ \Leftrightarrow x\ge0\\ c)4+x>5-3x\\ \Leftrightarrow x+3x>5-4\\ \Leftrightarrow4x>1\\ \Leftrightarrow x>\dfrac{1}{4}\\ d)-x+7\ge x-3\\ \Leftrightarrow x+x\le7+3\\ \Leftrightarrow2x\le10\\ \Leftrightarrow x\le\dfrac{10}{2}=5\)

Lời giải:
$4\times 5+3=23$
$6\times 7+3=45$
Vậy $(*)$ là phép toán nhân hai số đã cho với nhau rồi cộng thêm 3.
Áp dụng vào thì $9(*)10=9\times 10+3=93$

Bài 2:
\(a)\left(x-2\right)^2-\left(x+3\right)^2-4\left(x+1\right)=5\\ \Leftrightarrow\left(x^2-4x+4\right)-\left(x^2+6x+9\right)-4\left(x+1\right)=5\\ \Leftrightarrow x^2-4x+4-x^2-6x-9-4x-4=5\\ \Leftrightarrow-14x-9=5\\ \Leftrightarrow-14x=9+5=14\\ \Leftrightarrow x=\dfrac{14}{-14}\\ \Leftrightarrow x=-1\\ b)\left(5x+1\right)^2-\left(5x+3\right)\left(5x-3\right)=30\\ \Leftrightarrow\left(25x^2+10x+1\right)-\left(25x^2-9\right)=30\\ \Leftrightarrow25x^2+10x+1-25x^2+9=30\\ \Leftrightarrow10x+10=30\\ \Leftrightarrow10x=30-10\\ \Leftrightarrow10x=20\\ \Leftrightarrow x=\dfrac{20}{10}=2\)
Bài 1:
a: Sửa đề: \(A=6-2x+x^2\)
\(=x^2-2x+1+5\)
\(=\left(x-1\right)^2+5>=5\forall x\)
Dấu '=' xảy ra khi x-1=0
=>x=1
b: \(B=2x^2+3x-5\)
\(=2\left(x^2+\dfrac{3}{2}x-\dfrac{5}{2}\right)\)
\(=2\left(x^2+2\cdot x\cdot\dfrac{3}{4}+\dfrac{9}{16}-\dfrac{49}{16}\right)\)
\(=2\left(x+\dfrac{3}{4}\right)^2-\dfrac{49}{8}>=-\dfrac{49}{8}\forall x\)
Dấu '=' xảy ra khi \(x+\dfrac{3}{4}=0\)
=>\(x=-\dfrac{3}{4}\)
c: \(C=4x^2+8x+1\)
\(=4x^2+8x+4-3\)
\(=\left(2x+2\right)^2-3>=-3\forall x\)
Dấu '=' xảy ra khi 2x+2=0
=>2x=-2
=>x=-1

Lời giải:
\(B=\frac{-3}{4}.\frac{-8}{9}.\frac{-15}{16}....\frac{-99}{100}\\
=-\frac{3.8.15...99}{4.9...100}\) (do $B$ có lẻ các thừa số)
\(=-\frac{(1.3)(2.4)(3.5)...(9.11)}{2^2.3^2.4^2...10^2}\)
\(=-\frac{(1.2.3...9)(3.4.5...11)}{(2.3....10)(2.3.4...10)}\\ =-\frac{1.2.3...9}{2.3.4...10}.\frac{3.4.5...11}{2.3.4...10}\\ =-\frac{1}{10}.\frac{11}{2}=\frac{-11}{20}< \frac{-11}{21}\)

a: \(A=2xy^2\cdot\left(\dfrac{1}{2}x^2y^2x\right)\)
\(=2\cdot\dfrac{1}{2}\cdot xy^2\cdot x^3y^2=x^4y^4\)
b: Bậc là 8
c: \(A=x^4y^4\)
Hệ số là 1
Phần biến là \(x^4;y^4\)
d: Khi x=1 và y=-1 thì \(A=1^4\cdot\left(-1\right)^4=1\)
e: \(x^4>0\forall x\ne0;y^4>0\forall y\ne0\)
Do đó: \(x^4\cdot y^4>0\forall x,y\ne0\)
=>A luôn dương khi x,y đều khác 0
a)
\(A=2xy^2\cdot\left(\dfrac{1}{2}x^2y^2x\right)\\ =\left(2\cdot\dfrac{1}{2}\right)\cdot\left(x\cdot x^2\cdot x\right)\cdot\left(y^2\cdot y^2\right)\\ =x^4y^4\)
b) Bậc: 4 + 4 = 8
c) Hệ số là: 1
Phần biến là: `x^4y^4`
d) Thay x = 1 và y = -1 vào A ta có:
\(A=1^4\cdot\left(-1\right)^4=1\cdot1=1\)
e) Ta có: \(\left\{{}\begin{matrix}x^4>0\forall x>0\\y^4>0\forall y>0\end{matrix}\right.=>A=x^4y^4>0\cdot0=0\forall x,y>0\)
=> A luôn nhận giá trị nguyên khi x,y khác 0

a: Tỉ số giữa số thứ nhất và số thứ hai là:
\(\dfrac{1}{3}:\dfrac{1}{2}=\dfrac{1}{3}\times\dfrac{2}{1}=\dfrac{2}{3}\)
b: Tỉ số giữa số thứ nhất và số thứ hai là
\(\dfrac{3}{8}:\dfrac{2}{3}=\dfrac{3}{8}\times\dfrac{3}{2}=\dfrac{9}{16}\)
a) Tỉ số của số thứ nhất và số thứ hai là:
\(\dfrac{1}{3}:\dfrac{1}{2}=\dfrac{2}{3}\)
b) Tỉ số của số thứ nhất và số thứ hai là:
\(\dfrac{3}{8}:\dfrac{2}{3}=\dfrac{9}{16}\)


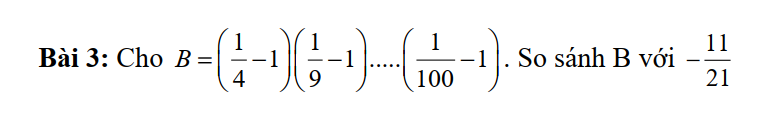
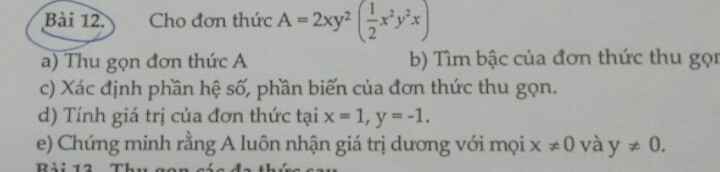

\(\dfrac{3}{x}+\dfrac{4}{x-1}=\dfrac{5x-2}{x^2-x}\left(x\notin\left\{0;1\right\}\right)\\ \Leftrightarrow\dfrac{3\left(x-1\right)}{x\left(x-1\right)}+\dfrac{4x}{x\left(x-1\right)}=\dfrac{5x-1}{x\left(x-1\right)}\\ \Leftrightarrow3\left(x-1\right)+4x=5x-1\\ \Leftrightarrow3x-3+4x=5x-1\\ \Leftrightarrow7x-3=5x+1\\ \Leftrightarrow7x-5x=1+3\\ \Leftrightarrow2x=4\\ \Leftrightarrow x=\dfrac{4}{2}\\ \Leftrightarrow x=2\left(tm\right)\)