Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


TA THẤY DÃY SỐ TRÊN CÓ 19 SỐ HẠNG
A= (0,1+1,9)x19:2
A=19

\(A=2+2^2+2^3+...+2^{99}+2^{100}\)
Ta có: \(2A=2^2+2^3+2^4+...+2^{100}+2^{101}\)
\(2A-A=\left(2^2+2^3+2^4+...+2^{100}+2^{101}\right)-\left(2+2^2+2^3+...+2^{99}+2^{100}\right)\)
\(A=2^{101}-2\)
Vì \(2^{101}=2^{101}\)
\(\Rightarrow2^{101}-2< 2^{101}\)
Hay \(A< 2^{101}\)
Vậy \(A< 2^{101}\).
\(#NqHahh\)
Trong phép chia có dư có thương là 1919, số chia là 77 và số dư là số lớn nhất có thể.
Số bị chia là

Giải:
Số dư là số dư lớn nhất có thể nên số dư là:
7 - 1 = 6
Số bị chia là:
19 x 7 + 6 = 139
Số bị chia là 139.

Cần số khoang chở người là:
973:(10x4)=24 (khoang)dư 13 hành khách
Vậy ta cần thêm 1 khoang để chứa 13 hành khách
Tổng là 25 khoang
Đ/s:...
Mỗi toa tàu hỏa có số chỗ ngồi là:
4 . 10=40 (chỗ)
Cần số toa tàu hỏa để chở hết số khách tham quan là:
973 : 40= 24 (toa dư 13 khách)
Vậy cần tất cả số toa tàu là:
24+1=25(toa)
Đ/S:...

Cần số khoang là: 818 : 4 = 204,5 (khoang)
Cần số toa tàu là: 204,5 : 10 = 20,45 (toa)
Số hơi lẻ nên mình cũng không chắc lắm

`#3107.101107`
`g)`
\(\dfrac{4}{19}\cdot\dfrac{-3}{7}+\dfrac{-3}{7}\cdot\dfrac{15}{19}+\dfrac{5}{7}\)
\(=\dfrac{-3}{7}\left(\dfrac{4}{19}+\dfrac{15}{19}\right)+\dfrac{5}{7}\)
\(=\dfrac{-3}{7}\cdot1+\dfrac{5}{7}\)
\(=-\dfrac{3}{7}+\dfrac{5}{7}=\dfrac{2}{7}\)
`h)`
\(\dfrac{5}{9}\cdot\dfrac{7}{13}+\dfrac{5}{9}\cdot\dfrac{9}{13}-\dfrac{5}{9}\cdot\dfrac{3}{13}\)
\(=\dfrac{5}{9}\cdot\left(\dfrac{7}{13}+\dfrac{9}{13}-\dfrac{3}{13}\right)\)
\(=\dfrac{5}{9}\cdot\left(\dfrac{7+9-3}{13}\right)\)
\(=\dfrac{5}{9}\cdot1=\dfrac{5}{9}\)
`i)`
\(\left(\dfrac{-4}{5}+\dfrac{4}{3}\right)+\left(\dfrac{-5}{4}+\dfrac{14}{5}\right)-\dfrac{7}{3}\)
\(=\dfrac{-4}{5}+\dfrac{4}{3}+\dfrac{-5}{4}+\dfrac{14}{5}-\dfrac{7}{3}\)
\(=\left(-\dfrac{4}{5}+\dfrac{14}{5}\right)+\left(\dfrac{4}{3}-\dfrac{7}{3}\right)-\dfrac{5}{4}\)
\(=\dfrac{10}{5}+\dfrac{-3}{3}-\dfrac{5}{4}\)
\(=2-1-\dfrac{5}{4}\)
\(=1-\dfrac{5}{4}\)
\(=-\dfrac{1}{4}\)
`j)`
\(\dfrac{8}{3}\cdot\dfrac{2}{5}\cdot\dfrac{3}{8}\cdot10\cdot\dfrac{19}{92}\)
\(=\left(\dfrac{8}{3}\cdot\dfrac{3}{8}\right)\cdot\left(\dfrac{2}{5}\cdot10\right)\cdot\dfrac{19}{92}\)
\(=1\cdot\dfrac{20}{5}\cdot\dfrac{19}{92}\)
\(=4\cdot\dfrac{19}{92}=\dfrac{19}{23}\)
`k)`
\(\dfrac{-5}{7}\cdot\dfrac{2}{11}+\dfrac{-5}{7}\cdot\dfrac{9}{14}+1\dfrac{5}{7}\)
\(=-\dfrac{5}{7}\cdot\dfrac{2}{11}-\dfrac{5}{7}\cdot\dfrac{9}{14}+1+\dfrac{5}{7}\)
\(=\dfrac{5}{7}\cdot\left(-\dfrac{2}{11}-\dfrac{9}{14}+1\right)+1\)
\(=\dfrac{5}{7}\cdot\dfrac{27}{154}+1\)
\(=\dfrac{135}{1078}+1=\dfrac{1213}{1078}\)
`l)`
\(\dfrac{12}{19}\cdot\dfrac{7}{15}\cdot\dfrac{-13}{17}\cdot\dfrac{19}{12}\cdot\dfrac{17}{13}\)
\(=\left(\dfrac{12}{19}\cdot\dfrac{19}{12}\right)\cdot\left(-\dfrac{13}{17}\cdot\dfrac{17}{13}\right)\cdot\dfrac{7}{15}\)
\(=1\cdot\left(-1\right)\cdot\dfrac{7}{15}=-\dfrac{7}{15}\)

Số số tự nhiên có thể lập được là:
5x4x3x2x1=120(số)

Lời giải:
Phản chứng, giả sử $a$ không cắt $b$. Suy ra $a\parallel b$
Mà: $a\perp Ox$
$\Rightarrow b\perp Ox$
Mà $b\perp Oy$
$\Rightarrow Ox\parallel Oy$
Điều này vô lý do $Ox$ cắt $Oy$ (bằng chứng là $\widehat{xOy}$ là góc nhọn)
Vậy điều giả sử là sai. Suy ra $a$ cắt $b$

Bài nào em chưa biết cách làm thì hỏi để Thầy cô và các bạn hướng dẫn. Em không gửi một tệp bài lên nhờ mọi người giải như vậy em sẽ không học tập phát triển được.
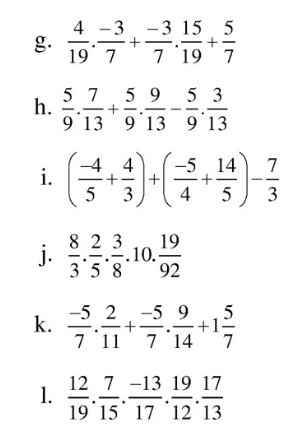


A = \(\dfrac{7}{23}\).\(\dfrac{5}{17}\) + \(\dfrac{7}{17}\).\(\dfrac{12}{23}\) + \(\dfrac{-30}{23}\)
A = \(\dfrac{7}{23}\).\(\dfrac{5}{17}\) + \(\dfrac{7}{23}\).\(\dfrac{12}{17}\) + \(\dfrac{-30}{23}\)
A = \(\dfrac{7}{23}\).(\(\dfrac{5}{17}\) + \(\dfrac{12}{17}\)) + \(\dfrac{-30}{23}\)
A = \(\dfrac{7}{23}\) - \(\dfrac{30}{23}\)
A = - 1