(x-1)(x+2)-2x-4=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
a. ĐKXĐ: $1-x\neq 0; 1+x\neq 0; 1-x^2\neq 0$
$\Leftrightarrow x\neq \pm 1$
b.
\(A=\frac{1+x}{(1-x)(1+x)}+\frac{2(1-x)}{(x+1)(1-x)}-\frac{5-x}{(1-x)(1+x)}\\ =\frac{1+x+(2-2x)-(5-x)}{(1-x)(1+x)}=\frac{-2}{(1-x)(1+x)}=\frac{-2}{1-x^2}\)

Lời giải:
$\frac{A}{B}=\frac{3}{5}\Rightarrow A=\frac{3}{5}B$
$\frac{B}{C}=\frac{7}{11}\Rightarrow C=\frac{11}{7}B$
$\frac{C}{D}=\frac{2}{3}\Rightarrow D=\frac{3}{2}C=\frac{3}{2}.\frac{11}{7}B=\frac{33}{14}B$
$A+B+C+D=1161$
$\frac{3}{5}B+B+\frac{11}{7}B+\frac{33}{14}B=1161$
$B.(\frac{3}{5}+1+\frac{11}{7}+\frac{33}{14})=1161$
$B.\frac{387}{70}=1161$
$B=210$

1008³ - 3.1008².8 + 3.1008.8² - 2⁹
= 1008³ - 3.1008².8 + 3.1008.8² - 8³
= (1008 - 8)³
= 1000³
= 1000000000

Lời giải:
a. $(3x+1)^2+(2-3x)(2+3x)$
$=(9x^2+6x+1)+(4-9x^2)=6x+5$
b.
$(2a-1)(4a^2+2a+1)-4a(2a^2-3)$
$=(2a)^3-1-(8a^3-12a)=8a^3-1-8a^3+12a=12a-1$

Vừa nãy làm sai:
Làm lại:
Số tiền giảm giá là:
\(12000000\text{x}10\%=1200000\left(\text{đồng}\right)\)
Giá tiền tivi sau khi giảm giá là:
\(12000000-1200000=10800000\left(\text{đồng}\right)\)
Đáp số: \(10800000\left(\text{đồng}\right)\)
Bài giải:
Giá tivi sau khi giảm giá là:
\(\dfrac{12000000\text{x}10}{100}=1200000\left(\text{đồng}\right)\)
Đáp số: \(1200000\text{đồng}\)

Lời giải:
Nếu $x=0$ thì: $0-6y^3=0\Rightarrow y=0$
Nếu $x\neq 0$. Đặt $y=tx$. Khi đó
PT $\Leftrightarrow x^3-6x^3t^3=x.tx(x-tx)$
$\Leftrightarrow x^3(1-6t^3)=x^3t(1-t)$
$\Leftrightarrow x^3[(1-6t^3)-t(1-t)]=0$
$\Leftrightarrow 1-6t^3-t+t^2=0$ (do $x\neq 0$)
$\Leftrightarrow 6t^3-t^2+t-1=0$
$\Leftrightarrow (2t-1)(3t^2+t+1)=0$
$\Leftrightarrow 2t-1=0$ hoặc $3t^2+t+1=0$
Dễ thấy $3t^2+t+1>0$ với mọi $t\in\mathbb{R}$
$\Rightarrow 2t-1=0\Leftrightarrow t=\frac{1}{2}$
Vậy $x=2y$. Đến đây bạn thay vào pt ban đầu để tìm $x,y$.
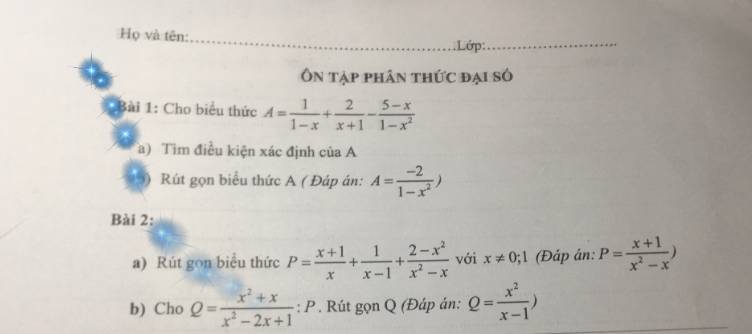
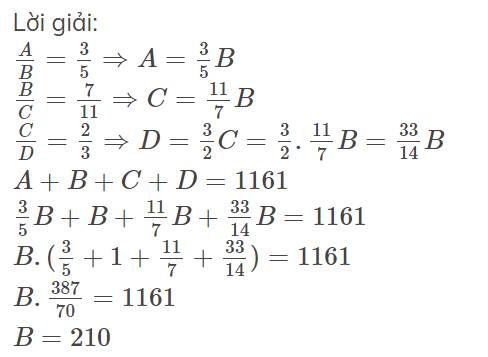
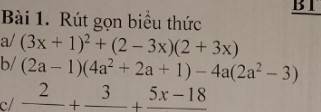
`#3107.101107`
`(x - 1)(x + 2) - 2x - 4 = 0`
`\Leftrightarrow (x - 1)(x + 2) - (2x + 4) = 0`
`\Leftrightarrow (x - 1)(x + 2) - 2(x + 2) = 0`
`\Leftrightarrow (x + 2)(x - 1 - 2) = 0`
`\Leftrightarrow (x + 2)(x - 3) = 0`
`\Leftrightarrow`\(\left[{}\begin{matrix}x+2=0\\x-3=0\end{matrix}\right.\)
`\Leftrightarrow`\(\left[{}\begin{matrix}x=-2\\x=3\end{matrix}\right.\)
Vậy, `x \in {-2; 3}.`
\(\left(x-1\right)\left(x+2\right)-2x-4=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)-\left(2x+4\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)-2\left(x+2\right)=0\)
\(\Leftrightarrow\left(x-1-2\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1-2=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x+2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0+3\\x=0-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-2\end{matrix}\right.\)
Vậy x=3 hoặc x=-2