2) Cho biểu thức A= 2023 ^ 1 + 2023 ^ 2 + 2023 ^ 3+...,+2023^ 009 +2023^ 10000.Chứng minh rằng 2022A + 2023 chia hếtcho 2023^2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đề sai. Cho $x=1,y=-1, z=0$ thì điều kiện đề cho vẫn đúng nhưng $x\neq y\neq z$

Số thứ hai + 5 = 3 lần số thứ ba
2 lần số thứ hai + 10 = 6 lần số thứ ba
Số thứ nhất = 6 lần số thứ ba
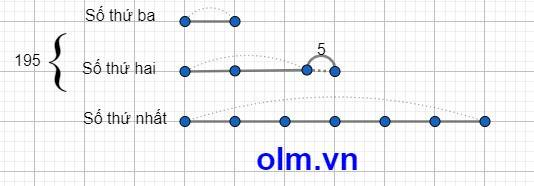
Theo sơ đồ ta có:
Số thứ ba là: (195 + 5) : (1 + 3 + 6) = 20
Số thứ hai là: 20 x 3 - 5 = 55
Số thứ nhất là: 55 x 2 + 10 = 120
Đáp số:..

Đây là dạng toán nâng cao hai tỉ số. Cấu trúc thi chuyên, thi học sinh giỏi, thi violympic.
Hôm nay olm.vn sẽ hướng dẫn các em giải dạng này như sau:
Giải:
Tỉ số số học sinh đội một và đội hai là:
\(\dfrac{2}{3}\) : \(\dfrac{4}{5}\) = \(\dfrac{5}{6}\)
Nếu mỗi bạn đội một trồng được một cây, mỗi bạn đội hai trồng được hai cây thì tỉ số số cây đội một và số cây đội hai là:
\(\dfrac{5}{6}\) : \(\dfrac{5}{4}\) = \(\dfrac{25}{24}\)
Ta có sơ đồ:
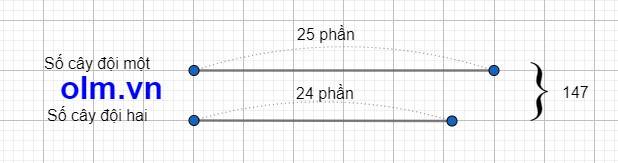
Theo sơ đồ ta có số cây đội một trồng được là:
147:(25+24)x25 = 75 (cây)
Số cây đội hai trồng được là:
147 - 75 = 72 (cây)
Số học sinh đội một là:
75 : 5 = 15 (học sinh)
Số học sinh đội hai là:
72 : 4 = 18 (học sinh)
Đáp số:...

Gọi m là số tự nhiên bớt đi cả tử và mẫu:
Theo đề bài ta có:
\(\dfrac{113-m}{138-m}=\dfrac{4}{5}\)
\(5\times\left(113-m\right)=4\times\left(138-m\right)\)
\(565-5\times m=552-4\times m\)
\(5\times m-4\times m=565-552\)
\(m\times\left(5-4\right)=13\)
\(m=13\)
Đáp số: ...

\(\dfrac{4\times4-6}{7\times4-8}=\dfrac{10}{20}=\dfrac{1}{2}\)
4 x 4 - 6 / 7 x 4 - 8
= 2 x 2 x 4 - 3 x 2 / 7 x 4 - 4 x 2
= 2 x (2 x 4 - 3) / 4 x (7 - 2)
= 2 x 5 / 4 x 5
=1/2

Gọi số thứ ba là x
Vì số thứ hai bằng 3 lần số thứ ba trừ đi 5 đơn vị nên Số thứ hai là 3x-5
Vì số thứ nhất bằng 2 lần số thứ hai cộng 10 đơn vị nên số thứ nhất là:
2(3x-5)+10=6x
Tổng của ba số là 195 nên ta có:
x+3x-5+6x=195
=>10x=200
=>x=20
=>Số thứ hai là \(3\cdot20-5=55\)
=>Số thứ nhất là \(2\cdot55+10=120\)
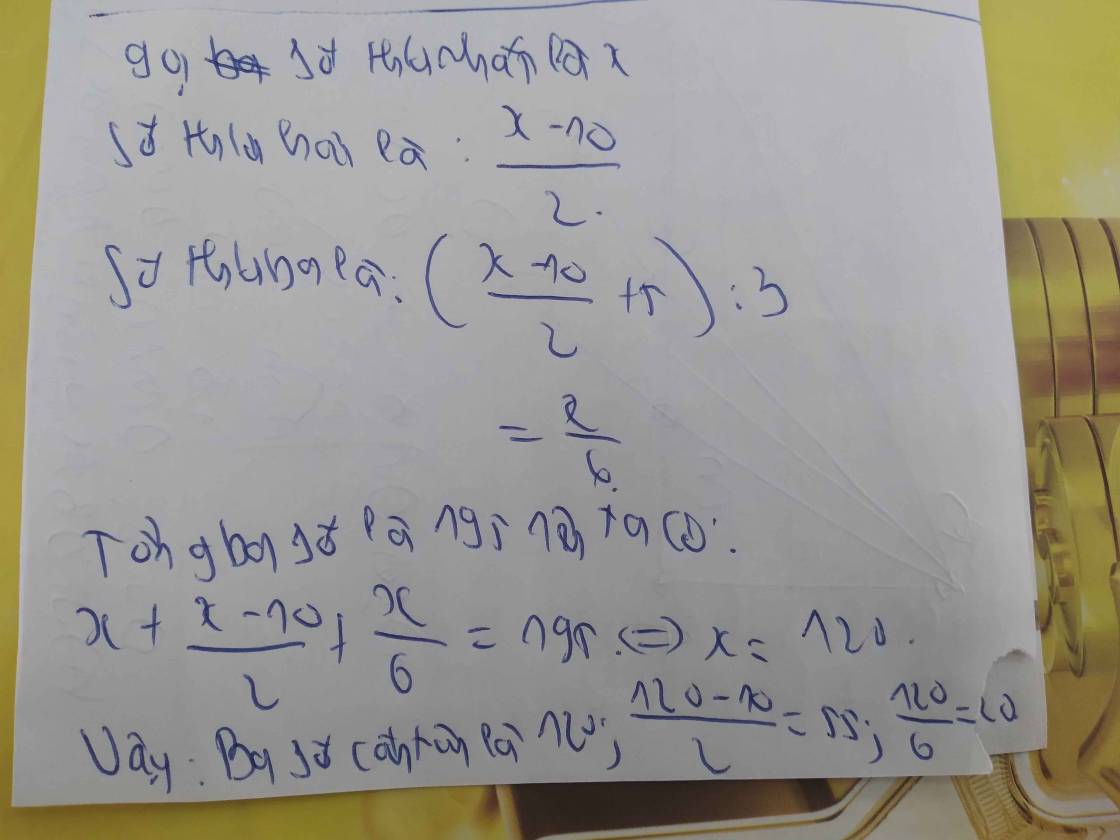


A = 2023 + 2023² + 2023³ + ... + 2023¹⁰⁰⁰⁰
⇒ 2023A = 2023² + 2023³ + 2023⁴ + ... + 2023¹⁰⁰⁰¹
⇒ 2022A = 2023A - A
= (2023² + 2023³ + 2023⁴ + ... + 2023¹⁰⁰⁰¹) - (2023 + 2023² + 2023³ + ... + 2023¹⁰⁰⁰⁰)
= 2023¹⁰⁰⁰¹ - 2023
⇒ 2022A + 2023 = 2023¹⁰⁰⁰¹ - 2023 + 2023
= 2023¹⁰⁰⁰¹
= 2023².2023⁹⁹⁹⁹ ⋮ 2023²
Vậy (2022A + 2023) ⋮ 2023²