\(\dfrac{x}{3}\) = \(\dfrac{5x}{15}\) = \(\dfrac{y}{4}\) = \(\dfrac{4y}{16}\) 

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

\(\dfrac{5x}{15}\) = \(\dfrac{4y}{16}\) = \(\dfrac{5x-4y}{15-16}\) = \(\dfrac{-5}{-1}\) = 5

\(x\) = 5 : \(\dfrac{5}{15}\) = 15

y = 5 : \(\dfrac{4}{16}\) = 20

Vậy (\(x;y\)) = (15; 20)

Chọn đáp án: D.Lê Thánh Tông

Giải thích:

Chính quyền phong kiến thời Lê sơ được hoàn thiện dần và hoàn chỉnh nhất dưới thời vua Lê Thánh Tông.

Trong những năm 1460 – 1471, Lê Thánh Tông tiến hành một cuộc cải cách hành chính lớn.

* Ở Trung ương:

- Đứng đầu là vua, trực tiếp nắm mọi quyền hành.

- Bãi bỏ một số chức quan cao cấp: tướng quốc, đại tổng quản, đại hành khiển.

- Giúp việc cho vua có các quan đại thần, 6 bộ và các cơ quan chuyên môn: Hàn lâm viện, Quốc sử viện, Ngự sử đài.

* Ở địa phương chia cả nước làm 13 đạo thừa tuyên.

Đáp án: A . Được mở rộng về phía Nam

Giải thích:

Lãnh thổ Đại Việt dưới thời vua Lê Thánh Tông được mở rộng hơn về phía Nam so với thời Trần:

- Lãnh thổ Đại Việt sau sự kiện năm 1306 vua Trần Nhân Tông gả công chúa Huyền Trần cho vua Chế Mân đổi lại sính lễ là hai châu Ô và Lý - tức vùng Thuận Hóa

- Năm 1471, sau khi chiếm vùng đất phía Nam Thuận Hóa cho đến đèo Cù Mông, vua Lê Thánh Tông lập thêm đơn vị hành chính thứ 13 - Đạo Thừa Tuyên Quảng Nam gồm 3 phủ: Thăng Hoa, Tư Nghĩa và Hoài Nhơn (nay là Quảng Nam, Quảng Ngãi, Bình Định).

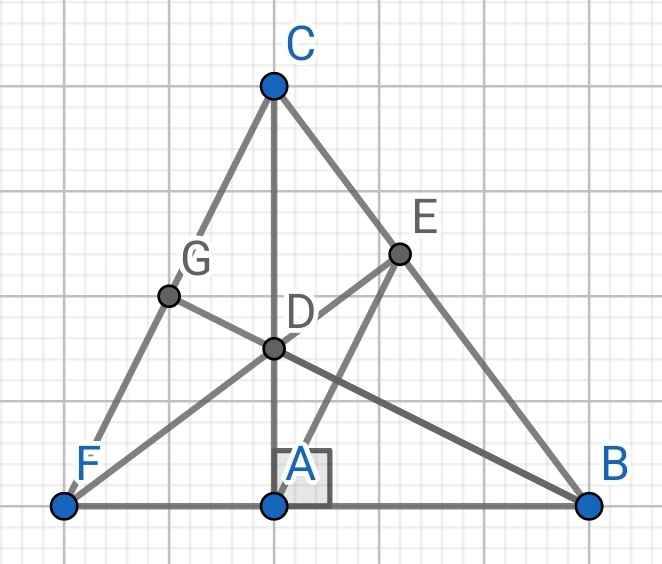
a) Do BD là tia phân giác của ∠ABC (gt)

⇒ ∠ABD = ∠CBD

⇒ ∠ABD = ∠EBD

Xét ∆BDA và ∆BDE có:

BD là cạnh chung

∠ABD = ∠EBD (cmt)

AB = BE (gt)

⇒ ∆BDA = ∆BDE (c-g-c)

b) Do ∆BDA = ∆BDE (cmt)

⇒ AD = DE (hai cạnh tương ứng)

⇒ D nằm trên đường trung trực của AE (1)

Do BA = BE (gt)

⇒ B nằm trên đường trung trực của AE (2)

Từ (1) và (2) ⇒ BD là đường trung trực của AE

⇒ BD ⊥ AE

c) Do ∆BAD = ∆BAE (cmt)

⇒ ∠BAD = ∠BED (hai góc tương ứng)

⇒ ∠BED = 90⁰

⇒ DE ⊥ BE

⇒ DE ⊥ BC

⇒ FE ⊥ BC

⇒ FE là đường cao của ∆BCF

Do CA AB (∆ABC vuông tại A)

⇒ CA ⊥ BF

⇒ CA là đường cao thứ hai của ∆BCF

Mà D là giao điểm của CA và FE

⇒ BD là đường cao thứ ba của ∆BCF

⇒ BD ⊥ CF

Mà BD ⊥ AE (cmt)

⇒ AE // CF

d) Do BD là tia phân giác của ∠ABC (gt)

⇒ BD là tia phân giác của ∠FBC

⇒ BD là đường phân giác của ∆BCF

∆BCF có:

BD là đường cao (cmt)

BD là đường phân giác (cmt)

⇒ ∆BCF cân tại B

⇒ BD là đường trung trực của ∆BCF

Mà M là trung điểm của CF (gt)

⇒ B, D, M thẳng hàng

           Giải:

a; Xét tam giác BDA và tam giác BDE có:

BA = BE (gt)

\(\widehat{ABD}\) = \(\widehat{DBE}\) (gt)

Cạnh BD (chung)

Vậy \(\Delta\) BDA = \(\Delta\) BDE (C-g-c)

b; Xét tam giác ABE có

   BA = BE (gt)

  ⇒ tam giác ABE cân tại B

 BD là phân giác của góc ABE (gt)

 ⇒ BD \(\perp\) AE (vì trong tam giác cân đường phân giác cũng là đường cao)

c; \(\Delta\) BDA = \(\Delta\) BDE (cmt)

⇒ \(\widehat{BAD}\) = \(\widehat{BED}\) = 90⁰

Xét tam giác vuông EBF và tam giác vuông ABC có:

      BE = AB

      \(\widehat{FBE}\) = \(\widehat{CBA}\)

⇒ \(\Delta\) EBF  =  \(\Delta\) ABC (góc nhọn, cạnh góc vuông)

⇒ BF = BC 

⇒ \(\Delta\) BFC  cân tại B

⇒ BD \(\perp\) FC (trong tam giác cân đường cao cũng là đường phân giác)

Mặt khác BD \(\perp\) AE (cmt)

⇒ AE // FC (vì hai đường thẳng cùng vuông góc đường thẳng thứ ba thì song song với nhau)

d; BD là phân giác của tam giác cân BFC nên BD là đường trung tuyến của FC, mà M là trung điểm CF vậy B, D, M thẳng hàng vì qua một đỉnh của tam giác chỉ kẻ được một trung tuyến ứng với cạnh đối diện của đỉnh đó. 

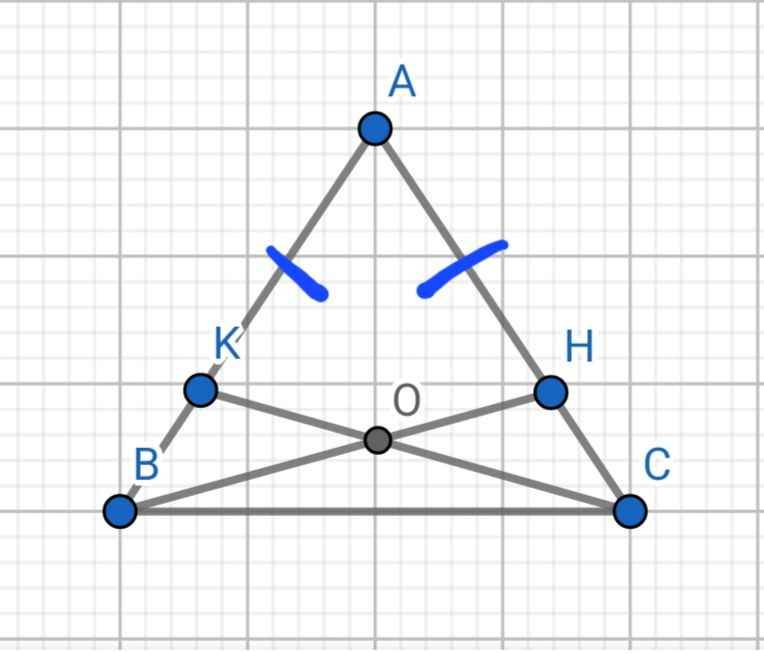
a: Xét ΔOAC và ΔOBC có 

OA=OB

\(\widehat{AOC}=\widehat{BOC}\)
OC chung

Do đó: ΔOAC=ΔOBC

b: TA có: ΔOAC=ΔOBC

=>\(\widehat{OAC}=\widehat{OBC}\)

=>\(\widehat{OAD}=\widehat{OBF}\)

Xét ΔOAD và ΔOBF có

\(\widehat{OAD}=\widehat{OBF}\)

OA=OB

\(\widehat{AOD}\) chung

Do đó: ΔOAD=ΔOBF

c: Ta có: \(\widehat{OAC}+\widehat{CAF}=180^0\)(kề bù)

\(\widehat{OBC}+\widehat{CBD}=180^0\)(kề bù)

mà \(\widehat{OAC}=\widehat{OBC}\)

nên \(\widehat{CAF}=\widehat{CBD}\)

Ta có; ΔOAD=ΔOBF

=>\(\widehat{ODA}=\widehat{OFB}\) và OD=OF

Ta có: OA+AF=OF

OB+BD=OD

mà OA=OB và OF=OD

nên AF=BD

Xét ΔCAF và ΔCBD có

\(\widehat{CAF}=\widehat{CBD}\)

AF=BD

\(\widehat{CFA}=\widehat{CDB}\)

Do đó; ΔCAF=ΔCBD

=>CF=CD và CA=CB

Ta có: OA=OB

=>O nằm trên đường trung trực của BA(1)

Ta có: CA=CB

=>C nằm trên đường trung trực của BA(2)

Từ (1),(2) suy ra OC là đường trung trực của BA

d: Ta có: OD=OF

=>O nằm trên đường trung trực của DF(3)

Ta có: CD=CF

=>C nằm trên đường trung trực của DF(4)

Ta có: MD=MF

=>M nằm trên đường trung trực của DF(5)

Từ (3),(4),(5) suy ra O,C,M thẳng hàng

chịu thôi em mới lớp 5

a: Ta có: \(\widehat{C}+\widehat{DEC}=90^0\)

\(\widehat{C}+\widehat{B}=90^0\)

Do đó: \(\widehat{DEC}=\widehat{B}\)

b: Xét ΔAFD và ΔAED có

AF=AE

\(\widehat{FAD}=\widehat{EAD}\)

AD chung

Do đó: ΔAFD=ΔAED

=>\(\widehat{AFD}=\widehat{AED}\)

mà \(\widehat{AFD}+\widehat{DFB}=180^0\)(hai góc kề bù)

và \(\widehat{AED}+\widehat{CED}=180^0\)(hai góc kề bù)

nên \(\widehat{DFB}=\widehat{CED}\)

=>\(\widehat{DFB}=\widehat{DBF}\)

=>ΔDBF cân tại D

c: Ta có: ΔAFD=ΔAED

=>DF=DE

mà DF=DB

nên DE=DB

Dù ai đi ngược về xuôi

Nhớ ngày giỗ tổ Mùng Mười Tháng Ba