có \(\Delta'=\left[-\left(m-1\right)\right]^2-m^2+m+5\)

\(\Delta'=m^2-2m+1-m^2+m+5\)

\(\Delta'=-m+6\)

để pt (1) có 2 nghiệm \(x_1;x_2\) \(\Leftrightarrow-m+6>0\)

\(\Leftrightarrow m< 6\)

theo định lí \(Vi-et\) \(\hept{\begin{cases}x_1+x_2=2m-2\\x_1.x_2=m^2-m-5\end{cases}}\)

theo bài ra \(\frac{x_1}{x_2}+\frac{x_2}{x_1}+\frac{10}{3}=0\)

\(\Leftrightarrow\frac{x_1^2+x_2^2}{x_1.x_2}+\frac{10}{3}=0\)   ( \(x_1.x_2\ne0\Leftrightarrow m^2-m-5\ne0\))

\(\Leftrightarrow\frac{\left(x_1+x_2\right)^2-2x_1.x_2}{x_1.x_2}=\frac{-10}{3}\)

\(\Leftrightarrow\frac{\left(2m-2\right)^2-2.\left(m^2-m-5\right)}{m^2-m-5}=-\frac{10}{3}\)

\(\Leftrightarrow\frac{4m^2-8m+4-2m^2+2m+10}{m^2-m-5}=\frac{-10}{3}\)

\(\Leftrightarrow\left(2m^2-6m+14\right).3=-10.\left(m^2-m-5\right)\)

\(\Leftrightarrow6.\left(m^2-3m+7\right)=-10.\left(m^2-m-5\right)\)

\(\Leftrightarrow-3m^2+9m-21=5m^2-5m-25\)

\(\Leftrightarrow-3m^2+9m-21-5m^2+5m+25=0\)

\(\Leftrightarrow-8m^2+14m+4=0\)

\(\Leftrightarrow4m^2-7m-2=0\)  \(\left(2\right)\)

từ PT (2) có \(\Delta=\left(-7\right)^2-4.4.\left(-2\right)=49+32=81>0\Rightarrow\sqrt{\Delta}=9\)

vì \(\Delta>0\) nên PT có 2 nghiệm phân biệt 

\(m_1=\frac{7-9}{8}=\frac{-1}{4}\)  ( TM ĐK 

\(m_2=\frac{7+9}{8}=2\)                                  \(m< 6\)và \(m^2-m-5\ne0\)) 

Bài này bạn áp dụng vi-ét là ra ngay nha !

Chúc bạn học tốt !

a) \(P=\left(\frac{x+8}{x\sqrt{x}+8}-\frac{1}{\sqrt{x}+2}\right):\left(1-\frac{x-3\sqrt{x}+6}{x-2\sqrt{x}+4}\right)\)

\(P=\frac{x+8-x+\sqrt{x}-4}{x\sqrt{x}+8}:\frac{x-2\sqrt{x}+4-x+3\sqrt{x}-6}{x-2\sqrt{x}+4}\)

\(P=\frac{\sqrt{x}+4}{x\sqrt{x}+8}:\frac{\sqrt{x}-2}{x-2\sqrt{x}+4}\)

\(P=\frac{\sqrt{x}+4}{\sqrt{x}+2}.\frac{1}{\sqrt{x}-2}\)

\(P=\frac{\sqrt{x}+4}{x-4}\)

b) Ta có \(x=6+4\sqrt{2}=2^2+2.2.\sqrt{2}+\left(\sqrt{2}\right)^2=\left(2+\sqrt{2}\right)^2\)

\(\Rightarrow\sqrt{x}=2+\sqrt{2}\)

Suy ra \(P=\frac{2+\sqrt{2}+4}{6+4\sqrt{2}-4}=\frac{6+\sqrt{2}}{4\sqrt{2}+2}=\frac{11\sqrt{2}-2}{14}\)

cô  Hoàng Thị Thu Huyền  ơi e thấy có j đó sai sai ở đây 

chỗ dòng thứ 2 phải là 

\(P=\left[\frac{8}{\left(\sqrt{x}+2\right)\left(x-2\sqrt{x}+4\right)}-\frac{x-2\sqrt{x}+4}{\left(\sqrt{x}+2\right)\left(x-2\sqrt{x}+4\right)}\right]\) 

vì theo hằng đẳng thức   A³ + B³= (A+B)(A²- AB +B²)

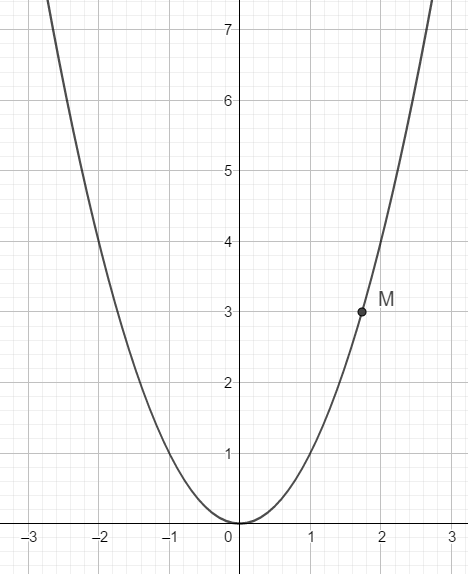
a) Do parabol qua điểm O nên ta có thể giả sử phương trình của Parabol có dạng : y = ax² \(\left(a\ne0\right)\)

Parabol qua điểm \(M\left(\sqrt{3};3\right)\) nên ta thấy ngay \(3=a\left(\sqrt{3}\right)^3\Rightarrow a=1\)

Vậy phương trình parabol là \(y=x^2\)

Ta có bảng giá trị: 

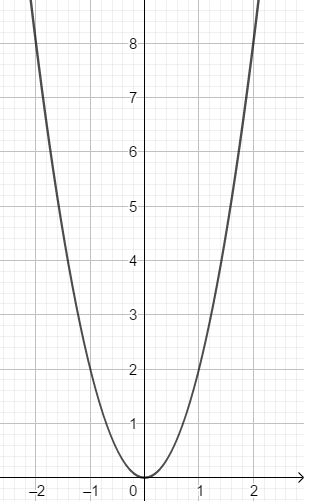
b) Vì \(K\left(\sqrt{2};4\right)\) thuộc parabol (P) nên \(4=a\left(\sqrt{2}\right)^2\Leftrightarrow a=2\)

Vậy phương trình parabol cần tìm là: \(y=2x^2\)

Bảng giá trị:

Cho BG cắt AC tại N, CG cắt AB tại P. Qua B kẻ đường thẳng song song với AC cắt CF,AF tại I,J. Qua C kẻ đường thẳng song song với AB cắt EB,EA tại D,H

\(\Delta BCA\)và \(\Delta CDB\)có : \(\widehat{ABC}=\widehat{BCD}\left(slt\right);\widehat{BAC}=\widehat{CBD}\)(góc tạo bởi tiếp tuyến & dây cung và góc nội tiếp cùng chắn cung BC) nên \(\Delta BCA\infty\Delta CDB\left(g.g\right)\). Suy ra : \(\frac{BC}{CD}=\frac{AB}{BC}\Leftrightarrow BC^2=AB.CD\left(1\right)\)

\(\Delta BCA\)và \(\Delta IBC\)có : \(\widehat{BCA}=\widehat{IBC}\left(slt\right);\widehat{BAC}=\widehat{ICB}\)(góc tạo bởi tiếp tuyến & dây cung và góc nội tiếp cùng chắn cung BC) nên \(\Delta BCA\infty\Delta IBC\left(g.g\right)\). Suy ra : \(\frac{BC}{IB}=\frac{CA}{BC}\Leftrightarrow BC^2=IB.CA\left(2\right)\)

\(\left(1\right),\left(2\right)\Rightarrow AB.CD=IB.CA\Leftrightarrow\frac{AB}{BI}=\frac{AC}{CD}\)

Áp dụng hệ quả định lí Talet : AC // IJ\(\Rightarrow\frac{AN}{JB}=\frac{FN}{FB}=\frac{CN}{BI}\Rightarrow BJ=BI\)(vì AN = CN)

AB // DH\(\Rightarrow\frac{PB}{CD}=\frac{EP}{EC}=\frac{AP}{HC}\Rightarrow CD=HC\)(vì PB = AP)

\(\frac{AB}{BI}=\frac{AC}{CD}\Leftrightarrow\frac{AB}{BJ}=\frac{AC}{CH}\). \(\widehat{JBA}=\widehat{CAB};\widehat{CAB}=\widehat{ACH}\left(slt\right)\Rightarrow\widehat{JBA}=\widehat{ACH}\)

\(\Delta ABJ,\Delta ACH\)có \(\widehat{JBA}=\widehat{HCA};\frac{AB}{BJ}=\frac{AC}{CH}\Rightarrow\Delta ABJ\infty\Delta ACH\left(c.g.c\right)\Rightarrow\widehat{AJB\:}=\widehat{AHC}\)

Mà \(\widehat{AJB\:}=\widehat{FAC};\widehat{AHC}=\widehat{EAB}\)(đồng vị) nên \(\widehat{EAB}=\widehat{FAC}\)

P/S : - Bài này là câu 7 của đề thi HSG Toán 9 Đà Nẵng 2017 - 2018 vào ngày 1/3 vừa qua. Mình bí bài này nhưng đã nhận được đáp án đề thi và muốn đưa bài giải cho mọi người tham khảo

- Link đáp án : www.facebook.com/toaji.phan/posts/595746860776994?pnref=story

- Link hình : www.facebook.com/toanhockhocothayanh/photos/a.258465918014842.1073741829.258088654719235/295108181017282/?type=3&theater

rảh nhỉ!hỏi rồi trả lời luôn!

\(2018x^2-2017-1=0\)

\(2018x^2-2018=0\)

\(2018\left(x^2-1\right)=0\)

\(\left(x-1\right)\left(x+1\right)=0\)

\(\Rightarrow\orbr{\begin{cases}x-1=0\\x+1=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=1\\x=-1\end{cases}}\)

đề phải là : 2018x^2-2017x-1 = 0

pt <=> (2018x^2-2018x)+(x-1) = 0

<=> 2018.x.(x-1)+(x-1) = 0

<=> (x-1).(2018x+1) = 0

<=> x-1=0 hoặc 2018x+1=0

<=> x=1 hoặc x=-1/2018

Vậy ............

Tk mk nha

Đường tròn c: Đường tròn qua B_1 với tâm O Góc α: Góc giữa O, A, P Góc α: Góc giữa O, A, P Góc β: Góc giữa P, B, O Góc β: Góc giữa P, B, O Đoạn thẳng i: Đoạn thẳng [P, C] Đoạn thẳng k: Đoạn thẳng [B, P] Đoạn thẳng l: Đoạn thẳng [P, A] Đoạn thẳng m: Đoạn thẳng [B, C] Đoạn thẳng n: Đoạn thẳng [E, B] Đoạn thẳng p: Đoạn thẳng [O, B] Đoạn thẳng q: Đoạn thẳng [O, A] Đoạn thẳng r: Đoạn thẳng [D, A] Đoạn thẳng s: Đoạn thẳng [A, B] O = (5.16, 0.8) O = (5.16, 0.8) O = (5.16, 0.8) O = (5.16, 0.8) O = (5.16, 0.8) O = (5.16, 0.8) O = (5.16, 0.8) P = (0.16, 5.34) P = (0.16, 5.34) P = (0.16, 5.34) P = (0.16, 5.34) P = (0.16, 5.34) P = (0.16, 5.34) P = (0.16, 5.34) Điểm A: Giao điểm đường của c, f Điểm A: Giao điểm đường của c, f Điểm A: Giao điểm đường của c, f Điểm A: Giao điểm đường của c, f Điểm A: Giao điểm đường của c, f Điểm A: Giao điểm đường của c, f Điểm A: Giao điểm đường của c, f Điểm B: Giao điểm đường của c, g Điểm B: Giao điểm đường của c, g Điểm B: Giao điểm đường của c, g Điểm B: Giao điểm đường của c, g Điểm B: Giao điểm đường của c, g Điểm B: Giao điểm đường của c, g Điểm B: Giao điểm đường của c, g Điểm C: Giao điểm đường của c, h Điểm C: Giao điểm đường của c, h Điểm C: Giao điểm đường của c, h Điểm C: Giao điểm đường của c, h Điểm C: Giao điểm đường của c, h Điểm C: Giao điểm đường của c, h Điểm C: Giao điểm đường của c, h Điểm D: Giao điểm đường của c, i Điểm D: Giao điểm đường của c, i Điểm D: Giao điểm đường của c, i Điểm D: Giao điểm đường của c, i Điểm D: Giao điểm đường của c, i Điểm D: Giao điểm đường của c, i Điểm D: Giao điểm đường của c, i Điểm E: Giao điểm đường của f, j Điểm E: Giao điểm đường của f, j Điểm E: Giao điểm đường của f, j Điểm E: Giao điểm đường của f, j Điểm E: Giao điểm đường của f, j Điểm E: Giao điểm đường của f, j Điểm E: Giao điểm đường của f, j

a) Do BC // AP nên \(\widehat{EPD}=\widehat{DCB}\)  (Hai góc so le trong)

mà \(\widehat{DCB}=\widehat{EBP}\) (Góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung BD)

nên \(\widehat{EPD}=\widehat{EPB}\)

Suy ra \(\Delta PED\sim\Delta BEP\left(g-g\right)\)

b) Ta thấy ngay \(\widehat{EAD}=\widehat{EBA}\) (Góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung AD)

Suy ra \(\Delta AED\sim\Delta BEA\left(g-g\right)\)

c) Do \(\Delta PED\sim\Delta BEP\Rightarrow\frac{PE}{BE}=\frac{ED}{PE}\Rightarrow PE^2=ED.EB\)

\(\Delta AED\sim\Delta BEA\Rightarrow\frac{AE}{BE}=\frac{ED}{AE}\Rightarrow AE^2=BE.ED\)

Vậy nên AE = EP

\(x^2+2x+1-4x^2=0\)

\(-3x^2+2x+1=0\)

\(3x^2-2x-1=0\)

\(3x^2-3x+x-1=0\)

\(3x\left(x-1\right)+\left(x-1\right)=0\)

\(\left(3x+1\right)\left(x-1\right)=0\)

\(\Rightarrow\orbr{\begin{cases}3x+1=0\\x-1=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=\frac{-1}{3}\\x=1\end{cases}}\)

\(x^2+2x+1-4x^2=0\)

\(\left(x+1\right)^2-\left(2x\right)^2=0\)

\(\left(x+1-2x\right)\left(x+1+2x\right)=0\)

\(\left(1-x\right)\left(3x+1\right)=0\)

\(\Rightarrow\orbr{\begin{cases}1-x=0\\3x+1=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=0\\x=\frac{-1}{3}\end{cases}}\)

Xét \(\Delta=\left[-2\left(m-1\right)\right]^2-4\left(m-3\right)=4\left(m-1\right)^2-4m+12\)

\(=4m^2-8m+4-4m+12\)

\(=4m^2-12m+16\)

\(=\left(2m+3\right)^2+7>0\forall m\)

Do \(\Delta>0\) nên PT trên luôn có hai nghiệm phân biệt \(\forall m\)

(a=1;b=-2(m-1);c=m-3)

Mà pt có 2 nghiệm với mọi m

=> Denta >0

<=>4(m-1)^2-4(m-3)>0

<=>4m^2-8m+4-4m+12>0

<=>4m^2-12m+16>0

<=>4m^2-12m+9+7>0

<=>(2m-3)^2+7>0

Ta thấy: \(\hept{\begin{cases}\left(2m-3\right)^2>0\\7>0\end{cases}\Rightarrow dpcm}\)

có \(\Delta=\left[2\left(m-2\right)\right]^2-4\left(-2m+1\right)\)

\(\Delta=4\left(m^2-4m+4\right)+8m-4\)

\(\Delta=4m^2-16m+16+8m-4\)

\(\Delta=4m^2-8m+12\)

\(\Delta=m^2-2m+3\)

\(\Delta=m^2-2m+1+2\)

\(\Delta=\left(m-1\right)^2+2>0\forall m\)

vì \(\Delta>0\forall m\)nên pt (1) luôn có 2 nghiệm phân biệt với mọi m 

3 phút

/3 phut