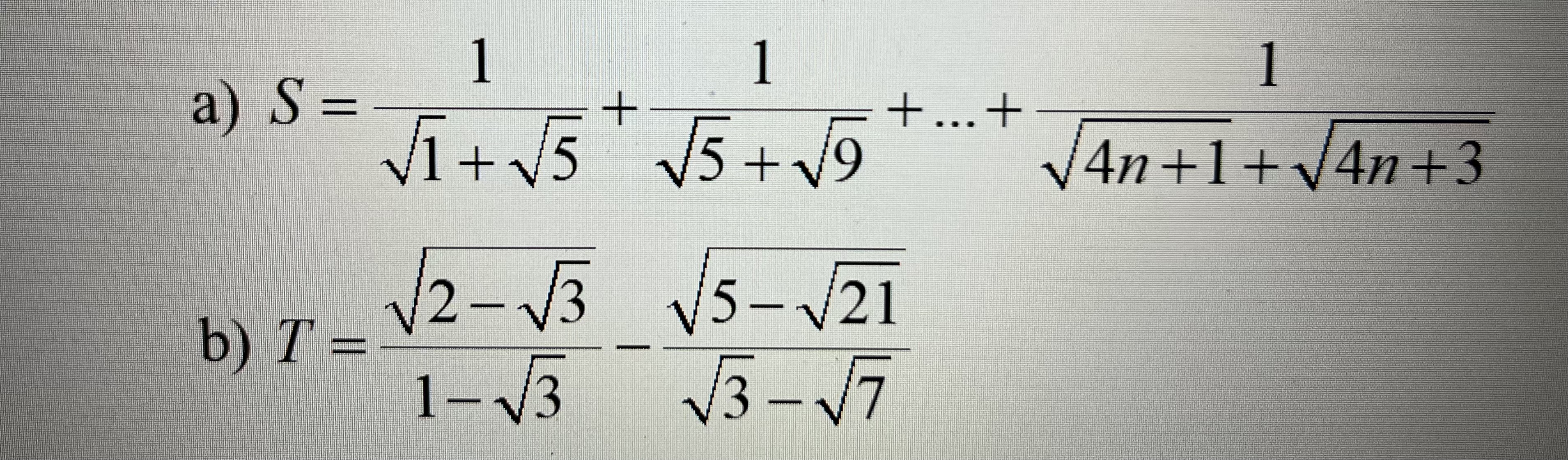sơ đồ khối minh họa cho bài toán giải phương trình bậc 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
12 tháng 4
\(\text{Δ}=5^2-4\left(m-3\right)=25-4m+12=-4m+37\)
Để phương trình có hai nghiệm thì Δ>=0
=>-4m+37>=0
=>-4m>=-37
=>\(m< =\dfrac{37}{4}\)
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-5\\x_1x_2=\dfrac{c}{a}=m-3\end{matrix}\right.\)
\(2x_1x_2-\left(x_1+x_2\right)=2\)
=>\(2\left(m-3\right)-\left(-5\right)=2\)
=>2m-6+5=2
=>2m-1=2
=>2m=3
=>\(m=\dfrac{3}{2}\left(nhận\right)\)
12 tháng 4
a: Sửa đề: \(S=\dfrac{1}{\sqrt{1}+\sqrt{5}}+\dfrac{1}{\sqrt{5}+\sqrt{9}}+...+\dfrac{1}{\sqrt{4n-3}+\sqrt{4n+1}}\)
\(=\dfrac{-\sqrt{1}+\sqrt{5}}{4}+\dfrac{-\sqrt{5}+\sqrt{9}}{4}+...+\dfrac{-\sqrt[]{4n-3}+\sqrt{4n+1}}{4}\)
\(=\dfrac{-\sqrt{1}+\sqrt{5}-\sqrt{5}+\sqrt{9}-...-\sqrt{4n-3}+\sqrt{4n+1}}{4}=\dfrac{\sqrt{4n+1}-1}{4}\)
b: \(T=\dfrac{\sqrt{2-\sqrt{3}}}{1-\sqrt{3}}-\dfrac{\sqrt{5-\sqrt{21}}}{\sqrt{3}-\sqrt{7}}\)
\(=\dfrac{1}{\sqrt{2}}\left(\dfrac{\sqrt{4-2\sqrt{3}}}{1-\sqrt{3}}-\dfrac{\sqrt{10-2\sqrt{21}}}{\sqrt{3}-\sqrt{7}}\right)\)
\(=\dfrac{1}{\sqrt{2}}\cdot\left(\dfrac{\sqrt{\left(\sqrt{3}-1\right)^2}}{1-\sqrt{3}}-\dfrac{\sqrt{\left(\sqrt{7}-\sqrt{3}\right)^2}}{\sqrt{3}-\sqrt{7}}\right)\)
\(=\dfrac{1}{\sqrt{2}}\cdot\left(\dfrac{\sqrt{3}-1}{1-\sqrt[]{3}}-\dfrac{\sqrt{7}-\sqrt{3}}{\sqrt{3}-\sqrt{7}}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(-1+\dfrac{\sqrt{7}-\sqrt{3}}{\sqrt{7}-\sqrt{3}}\right)=0\)