Thiếu hình đồ thị rồi em

\(-x^3+3x-7+2m=0\)

\(\Leftrightarrow x^3-3x+7=2m\)

Xét hàm: \(f\left(x\right)=x^3-3x+7\)

\(f'\left(x\right)=3x^2-3=0\Rightarrow x=\pm1\)

Bảng biến thiên:

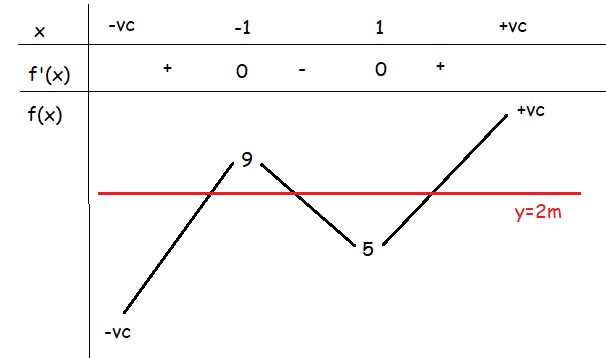
Từ BBT ta thấy pt có 3 nghiệm pb hay \(y=2m\) cắt \(y=f\left(x\right)\) tại 3 điểm pb

\(\Leftrightarrow5< 2m< 9\Rightarrow\dfrac{5}{2}< m< \dfrac{9}{2}\)

Gọi \(A_1\) là biến cố: "2 sản phẩm lấy nhầm từ lô 1 đều là sản phẩm tốt"

\(A_2\) là biến cố: "2 sản phẩm lấy nhầm từ lô 1 có 1 sản phẩm tốt 1 sản phẩm xấu"

`A_3` là biến cố: "2 sản phẩm lấy nhầm từ lô 1 đều là sản phẩm xấu"

\(\Rightarrow P\left(A_1\right)=\dfrac{C_6^2}{C_9^2}=\dfrac{5}{12}\); \(P\left(A_2\right)=\dfrac{C_6^1.C_3^1}{C_9^2}=\dfrac{1}{2}\); \(P\left(A_3\right)=\dfrac{C_3^2}{C_9^2}=\dfrac{1}{12}\)

\(A_1;A_2;A_3\) tạo thành 1 nhóm biến cố đầy đủ

Gọi B là biến cố: "sản phẩm cuối cùng lấy ra là sản phẩm tốt"

\(\Rightarrow P\left(B|A_1\right)=\dfrac{5+2}{7+2}=\dfrac{7}{9}\);

 \(P\left(B|A_2\right)=\dfrac{5+1}{7+2}=\dfrac{2}{3}\);

 \(P\left(B|A_3\right)=\dfrac{5}{7+2}=\dfrac{5}{9}\)

a.

\(P\left(B\right)=P\left(A_1\right).P\left(B|A_1\right)+P\left(A_2\right).P\left(B|A_2\right)+P\left(A_3\right).P\left(B|A_3\right)\)

\(=\dfrac{5}{12}.\dfrac{7}{9}+\dfrac{1}{2}.\dfrac{2}{3}+\dfrac{1}{12}.\dfrac{5}{9}=\dfrac{19}{27}\)

b.

Gọi `C_1` là biến cố "sản phẩm cuối cùng lấy ra thuộc lô 1"

`C_2` là biến cố: "sản phẩm cuối cùng lấy ra thuộc lô 2"

\(\Rightarrow P\left(C_1\right)=\dfrac{2}{9};P\left(C_2\right)=\dfrac{7}{9}\)

`C_1`, `C_2` cũng là nhóm biến cố đầy đủ

\(P\left(B|C_1\right)=\dfrac{6}{9}=\dfrac{2}{3}\)

\(\Rightarrow P\left(C_1|B\right)=\dfrac{P\left(B|C_1\right).P\left(C_1\right)}{P\left(B\right)}=\dfrac{\dfrac{2}{3}.\dfrac{2}{9}}{\dfrac{19}{27}}=\dfrac{4}{19}\)

c.

\(P\left(A_2|B\right)=\dfrac{P\left(B|A_2\right).P\left(A_2\right)}{P\left(B\right)}=\dfrac{\dfrac{2}{3}.\dfrac{1}{2}}{\dfrac{19}{27}}=\dfrac{9}{19}\)

 Gọi A, B, C lần lượt là các biến cố: "Khách hàng trả lời "sẽ sử dụng"."; "Khách hàng trả lời "có thể sẽ sử dụng"." và "Khách hàng trả lời "không sử dụng"." và X là biến cố: "Khách hàng sử dụng dịch vụ."

 Khi đó theo đề bài, ta có \(P\left(A\right)=\dfrac{17}{100};P\left(B\right)=\dfrac{48}{100};P\left(C\right)=\dfrac{35}{100};P\left(X|A\right)=0,4;P\left(X|B\right)=0,2;P\left(X|C\right)=0,01\)

 Theo công thức xác suất đầy đủ: 

\(P\left(X\right)=P\left(A\right)P\left(X|A\right)+P\left(B\right)P\left(X|B\right)+P\left(C\right)P\left(X|C\right)\)

\(=\dfrac{17}{100}.0,4+\dfrac{48}{100}.0,2+\dfrac{35}{100}.0,01=\dfrac{67}{400}=0,1675=16,75\%\)

Vậy tỉ lệ khách hàng sử dụng dịch vụ là \(16,75\%\)

Gọi \(A_1\) là biến cố: "khách hàng được chọn thuộc nhóm trả lời sẽ sử dụng"

`A_2` là biến cố: "khách hàng được chọn thuộc nhóm trả lời có thể sẽ sử dụng"

`A_3` là biến cố: "khách hàng được chọn thuộc nhóm trả lời không sử dụng"

\(\Rightarrow P\left(A_1\right)=\dfrac{17}{100}\) ; \(P\left(A_2\right)=\dfrac{48}{100}\); \(P\left(A_3\right)=\dfrac{35}{100}\)

\(A_1;A_2;A_3\) tạo thành 1 nhóm biến cố đầy đủ

Gọi B là biến cố: "khách hàng đó sử dụng dịch vụ của công ty"

\(\Rightarrow P\left(B|A_1\right)=0,4\); \(P\left(B|A_2\right)=0,2\); \(P\left(B|A_3\right)=0,01\)

Theo công thức xác suất đầy đủ:

\(P\left(B\right)=0,4\times\dfrac{17}{100}+0,2\times\dfrac{48}{100}+0,01\times\dfrac{35}{100}=0,1675\)

\(\overrightarrow{AB}=\left(1;1-3\right)\), \(\overrightarrow{AC}=\left(-1;2;-5\right)\)

\(\left[\overrightarrow{AB},\overrightarrow{AC}\right]=\left(1,8,3\right)\)

\(\Rightarrow\left(ABC\right)\) nhận (1,8,3) là 1 ptvt

Phương trình:

\(1\left(x-5\right)+8\left(y-1\right)+3\left(z-4\right)=0\)

\(\Leftrightarrow x+8y+3z-25=0\)

\(\overrightarrow{AB}=\left(2;1;-2\right)\) ; \(\overrightarrow{AC}=\left(-12;6;0\right)\)

\(\left[\overrightarrow{AB},\overrightarrow{AC}\right]=\left(12;24;24\right)=12.\left(1;2;2\right)\)

\(\Rightarrow\left(ABC\right)\) nhận (1,2,2) là 1 vtpt

Phương trình:

\(1\left(x-2\right)+2\left(y+1\right)+2\left(z-3\right)=0\)

\(\Leftrightarrow x+2y+2z-6=0\)

\(\overrightarrow{DE}=\left(-1;1;2\right)\); \(\overrightarrow{DF}=\left(2;-1;-1\right)\)

\(\left[\overrightarrow{DE},\overrightarrow{DF}\right]=\left(1;3;-1\right)\)

\(\Rightarrow\left(DEF\right)\) nhận (1;3;-1) là 1 vtpt

Phương trình:

\(1\left(x-3\right)+3\left(y-0\right)-1\left(z-2\right)=0\)

\(\Leftrightarrow x+3y-z-1=0\)