Tan a=2 tính Cos^2a
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(0< a< \dfrac{\Omega}{2}\)
=>\(sina>0\)
=>\(sina=\sqrt{1-cos^2a}=\dfrac{4}{5}\)
\(\dfrac{3}{2}\Omega< b< 2\Omega\)
=>\(sinb< 0\)
=>\(sinb=-\sqrt{1-\left(\dfrac{12}{13}\right)^2}=-\dfrac{5}{13}\)
\(tana=\dfrac{sina}{cosa}=\dfrac{4}{5}:\dfrac{3}{5}=\dfrac{4}{3}\)
\(tanb=\dfrac{sinb}{cosb}=\dfrac{-5}{13}:\dfrac{12}{13}=-\dfrac{5}{12}\)
\(tan\left(a+b\right)=\dfrac{tana+tanb}{1-tana\cdot tanb}\)
\(=\dfrac{\dfrac{4}{3}+\dfrac{-5}{12}}{1-\dfrac{4}{3}\cdot\dfrac{-5}{12}}=\dfrac{11}{12}:\left(1+\dfrac{20}{36}\right)=\dfrac{11}{12}:\dfrac{14}{9}\)
\(=\dfrac{11}{12}\cdot\dfrac{9}{14}=\dfrac{11\cdot3}{4\cdot14}=\dfrac{33}{56}\)

a) \(\lim\limits_{ }\left(\sqrt{n^2-n+1}-n\right)\)
\(=\lim\limits_{ }\left[\dfrac{\left(\sqrt{n^2-n+1}-n\right)\left(\sqrt{n^2-n+1}+n\right)}{\sqrt{n^2-n+1}+n}\right]\)
\(=\lim\limits_{ }\left(\dfrac{1-n}{\sqrt{n^2-n+1}+n}\right)\)
\(=\lim\limits_{ }\left(\dfrac{\dfrac{1}{n}-1}{\sqrt{1-\dfrac{1}{n}+\dfrac{1}{n^2}}+1}\right)\)
\(=-\dfrac{1}{2}\)
b) \(\lim\limits_{ }\left(\dfrac{-3}{4n^2-2n+1}\right)=0\)
c) \(\lim\limits_{ }\dfrac{n^2+n+5}{2n+1}=+\infty\)
d) \(\lim\limits_{ }\left(\sqrt{n^2-1}-\sqrt{3n^2+2}\right)\)
\(=\lim\limits_{ }\left(\dfrac{-2n^2-3}{\sqrt{n^2-1}+\sqrt{3n^2+2}}\right)\)
\(\lim\limits_{ }\left(\dfrac{-2n-\dfrac{3}{n}}{\sqrt{1-\dfrac{1}{n^2}}+\sqrt{3+\dfrac{2}{n^2}}}\right)\)
\(=-\infty\)
a: \(lim\left(\sqrt{n^2-n+1}-n\right)\)
\(=\lim\limits\dfrac{n^2-n+1-n^2}{\sqrt{n^2-n+1}+n}=\lim\limits\dfrac{-n+1}{\sqrt{n^2-n+1}+n}\)
\(=\lim\limits\dfrac{-1+\dfrac{1}{n}}{\sqrt{1-\dfrac{1}{n}+\dfrac{1}{n^2}}+1}=\dfrac{-1+0}{\sqrt{1-0+0}+1}=\dfrac{-1}{2}\)
b: \(\lim\limits\dfrac{-3}{4n^2-2n+1}\)
\(=\lim\limits\dfrac{-\dfrac{3}{n^2}}{4-\dfrac{2}{n}+\dfrac{1}{n^2}}=\dfrac{0}{4-0+0}=0\)
c: \(\lim\limits\dfrac{n^2+n+5}{2n+1}=\lim\limits\dfrac{n^2\left(1+\dfrac{1}{n}+\dfrac{5}{n^2}\right)}{n\left(2+\dfrac{1}{n}\right)}\)
\(=\lim\limits\dfrac{n\left(1+\dfrac{1}{n}+\dfrac{5}{n^2}\right)}{2+\dfrac{1}{n}}=+\infty\)
d: \(\lim\limits\left(\sqrt{n^2-1}-\sqrt{3n^2+2}\right)\)
\(=\lim\limits\left(\dfrac{n^2-1-3n^2-2}{\sqrt{n^2-1}+\sqrt{3n^2+2}}\right)=\lim\limits\left(\dfrac{-2n^2-3}{\sqrt{n^2-1}+\sqrt{3n^2+2}}\right)\)
\(=\lim\limits\left(\dfrac{n^2\left(-2-\dfrac{3}{n^2}\right)}{n\cdot\left(\sqrt{1-\dfrac{1}{n^2}}+\sqrt{3+\dfrac{2}{n^2}}\right)}\right)\)
\(=\lim\limits\left(\dfrac{n\left(-2-\dfrac{3}{n^2}\right)}{\sqrt{1-\dfrac{1}{n^2}}+\sqrt{3+\dfrac{2}{n^2}}}\right)=+\infty\)

\(\dfrac{sin^3x+sinx\cdot cos^2x-cosx}{1-2\cdot sinx\cdot cosx}\)
\(=\dfrac{sinx\left(sin^2x+cos^2x\right)-cosx}{\left(sinx-cosx\right)^2}\)
\(=\dfrac{sinx-cosx}{\left(sinx-cosx\right)^2}=\dfrac{1}{sinx-cosx}\)

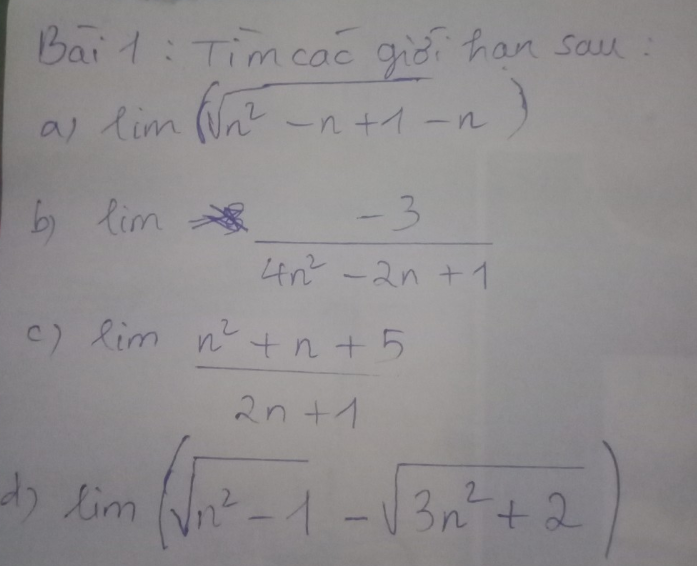


\(1+tan^2\alpha=\dfrac{1}{cos^2\alpha}\Rightarrow1+2^2=\dfrac{1}{cos^2\alpha}\\ \Rightarrow5=\dfrac{1}{cos^2\alpha}\Rightarrow cos^2\alpha=\dfrac{1}{5}\)