
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Khi x=-1;y=-1;z=-1 thì \(N=\left(-1\right)^1\cdot\left(-1\right)^2\cdot\left(-1\right)^3+\left(-1\right)^2\cdot\left(-1\right)^3\cdot\left(-1\right)^4+...+\left(-1\right)^{2014}\cdot\left(-1\right)^{2015}\cdot\left(-1\right)^{2016}\)
=1-1+1-1+...+1-1
=0

a: Xét ΔABH vuông tại A và ΔEBH vuông tại E có
BH chung
\(\widehat{ABH}=\widehat{EBH}\)
Do đó: ΔBAH=ΔBEH
b: Xét ΔBFC có
FE,CA là các đường cao
FE cắt CA tại H
Do đó: H là trực tâm của ΔBFC
c: Xét ΔBEF vuông tại E và ΔBAC vuông tại A có
BE=BA
\(\widehat{EBF}\) chung
Do đó ΔBEF=ΔBAC
=>BF=BC
=>ΔBFC cân tại B
Ta có: ΔBFC cân tại B
mà BH là đường cao
nên BH là đường trung tuyến của ΔBFC
=>K là trung điểm của FC
Xét ΔMAQ và ΔMFK có
MA=MF
\(\widehat{AMQ}=\widehat{FMK}\)(hai góc đối đỉnh)
MQ=MK
Do đó: ΔMAQ=ΔMFK
=>\(\widehat{MAQ}=\widehat{MFK}\)
=>AQ//FK
=>AQ//FC
Xét ΔBFC có \(\dfrac{BA}{BF}=\dfrac{BE}{BC}\)
nên AE//FC
mà AQ//FC
và AE,AQ có điểm chung là A
nên A,E,Q thẳng hàng

a: Xét ΔAIB và ΔAIC có
AB=AC
BI=CI
AI chung
Do đó: ΔAIB=ΔAIC
b: ΔABI=ΔACI
=>\(\widehat{AIB}=\widehat{AIC}\)
mà \(\widehat{AIB}+\widehat{AIC}=180^0\)
nên \(\widehat{AIB}=\widehat{AIC}=\dfrac{180^0}{2}=90^0\)
=>AI\(\perp\)BC
Xét ΔDBC có
DI là đường cao
DI là đường trung tuyến
Do đó: ΔDBC cân tại D
=>DB=DC
c: Ta có: DB=DE
mà D nằm giữa B và E
nên D là trung điểm của BE
Xét ΔEBC có
EI,CD là các đường trung tuyến
EI cắt CD tại G
Do đó: G là trọng tâm của ΔEBC
=>EG=2GI

Gọi độ dài quãng đường AB là x(km)
(Điều kiện: x>0)
Thời gian ô tô thứ nhất đi từ A đến B là \(\dfrac{x}{30}\left(giờ\right)\)
Thời gian ô tô thứ hai đi từ A đến B là \(\dfrac{x}{60}\left(giờ\right)\)
Ô tô thứ hai đến B trước ô tô thứ nhất 3 giờ nên ta có:
\(\dfrac{x}{30}-\dfrac{x}{60}=3\)
=>\(\dfrac{x}{60}=3\)
=>x=180(nhận)
Thời gian ô tô thứ nhất đi là 180/60=3(giờ)
Thời gian ô tô thứ hai đi là 180/30=6(giờ)

Gọi chiều dài, chiều rộng, chiều cao lần lượt là a(cm),b(cm),c(cm)
(ĐIều kiện: a>0; b>0; c>0)
Chiều dài; chiều rộng; chiều cao lần lượt tỉ lệ với 4;3;2
=>\(\dfrac{a}{4}=\dfrac{b}{3}=\dfrac{c}{2}=k\)
=>a=4k; b=3k; c=2k
Thể tích là 192cm3 nên \(a\cdot b\cdot c=192\)
=>\(4k\cdot3k\cdot2k=192\)
=>\(24k^3=192\)
=>\(k^3=8\)
=>\(k=2\)
=>\(a=4\cdot2=8;b=3\cdot2=6;c=2\cdot2=4\)
Diện tích xung quanh là:
(8+6)x2x4=8x14=112(cm2)

Thể tích của của thùng là:
40x25x30=30000(cm3)
Thời gian hết lượng nước là:
30000:1500=20(giờ)

a: \(f\left(x\right)⋮g\left(x\right)\)
=>\(2x^2-x+2⋮x+1\)
=>\(2x^2+2x-3x-3+5⋮x+1\)
=>\(5⋮x+1\)
=>\(x+1\in\left\{1;-1;5;-5\right\}\)
=>\(x\in\left\{0;-2;4;-6\right\}\)
b: \(f\left(x\right)⋮g\left(x\right)\)
=>\(3x^2-4x+6⋮3x-1\)
=>\(3x^2-x-3x+1+5⋮3x-1\)
=>\(5⋮3x-1\)
=>\(3x-1\in\left\{1;-1;5;-5\right\}\)
=>\(3x\in\left\{2;0;6;-4\right\}\)
=>\(x\in\left\{\dfrac{2}{3};0;2;-\dfrac{4}{3}\right\}\)
mà x nguyên
nên \(x\in\left\{0;2\right\}\)
c: \(f\left(x\right)⋮g\left(x\right)\)
=>\(-2x^3-7x^2-5x+5⋮x+2\)
=>\(-2x^3-4x^2-3x^2-6x+x+2+3⋮x+2\)
=>\(3⋮x+2\)
=>\(x+2\in\left\{1;-1;3;-3\right\}\)
=>\(x\in\left\{-1;-3;1;-5\right\}\)

Bổ sung đề: ΔABC vuông tại A
a: Xét ΔEAB và ΔEND có
EA=EN
\(\widehat{AEB}=\widehat{NED}\)(hai góc đối đỉnh)
EB=ED
Do đó: ΔEAB=ΔEND
=>\(\widehat{EAB}=\widehat{END}\)
=>AB//ND
b: Ta có: AB//ND
AB\(\perp\)AC
Do đó: ND\(\perp\)AC
Ta có: ΔABC vuông tại A
mà AD là đường trung tuyến
nên \(AD=\dfrac{BC}{2}=AB=BD\)
=>ΔABD đều
Ta có: ΔABD đều
mà AE là đường trung tuyến
nên AE\(\perp\)BD
Xét ΔANC có
CE,ND là các đường cao
CE cắt ND tại D
Do đó: D là trực tâm của ΔANC
=>AD\(\perp\)NC
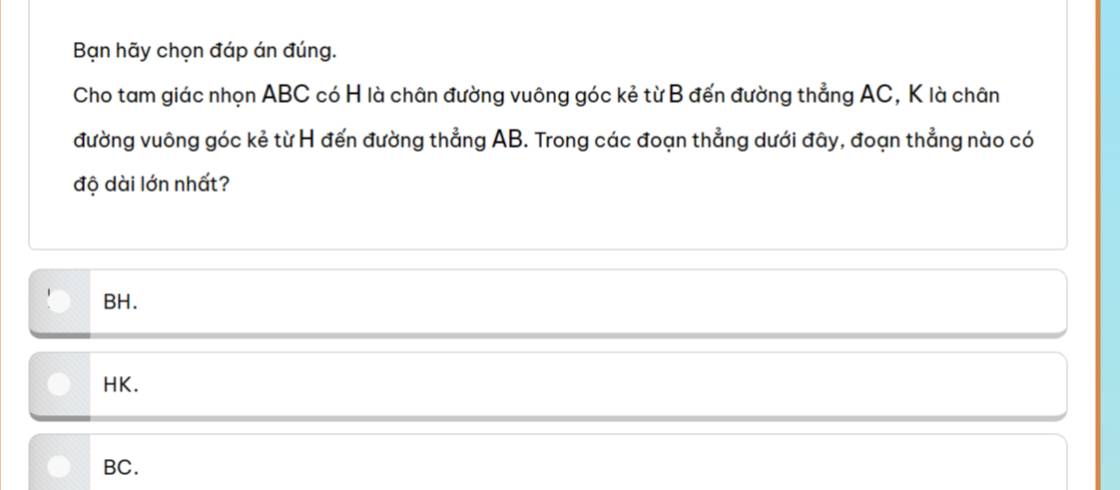 help me, please~
help me, please~

a; \(\dfrac{x}{8}\) = \(\dfrac{y}{-5}\) và \(x\) + y = 15
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{8}\) = \(\dfrac{y}{-5}\) = \(\dfrac{x+y}{8-5}\) = \(\dfrac{15}{3}\) = 5
\(x\) = 5.8 = 40
y = 5.(-5)
y = - 25
Vậy (\(x;y\)) = ( 40; - 25)
b; Giải:
Một máy in hết số bao bì trong: 6 x 4 = 24 (giờ)
Thực tế số máy in số bao bì là: 6 - 2 = 4 (máy)
Nếu bị hỏng 4 máy thì sẽ in xong số bao bì trong:
24 : 4 = 6 (giờ)
Kết luận nếu bị hỏng hai máy thì xưởng in sẽ in hết số bao bì trong 6 giờ.