ai giúp mình bài này với :)))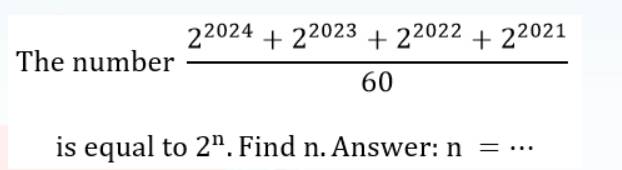
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(\dfrac{2^4\cdot125}{2^7\cdot50}=\dfrac{2^4\cdot5^3}{2^8\cdot5^2}=\dfrac{5}{2^4}=\dfrac{5}{16}\)

a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
b: Ta có: ΔBAD=ΔBED
=>\(\widehat{BAD}=\widehat{BED}\)
mà \(\widehat{BAD}=90^0\)
nên \(\widehat{BED}=90^0\)
c: ta có: \(\widehat{BED}=90^0\)
=>DE\(\perp\)BC
d: ta có: ΔBAD=ΔBED
=>DA=DE
mà DE<DC(ΔDEC vuông tại E)
nên DA<DC
=>DC>DA

a: \(P=\dfrac{x}{x-2}+\dfrac{2-x}{x+2}+\dfrac{8-6x}{x^2-4}\)
\(=\dfrac{x}{x-2}-\dfrac{x-2}{x+2}+\dfrac{8-6x}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x\left(x+2\right)-\left(x-2\right)^2+8-6x}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x^2+2x-x^2+4x-4+8-6x}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{4}{\left(x-2\right)\left(x+2\right)}=\dfrac{4}{x^2-4}\)
b: Thay x=3 vào P, ta được:
\(P=\dfrac{4}{3^2-4}=\dfrac{4}{5}\)
Thay x=-1/2 vào P, ta được:
\(P=\dfrac{4}{\left(-\dfrac{1}{2}\right)^2-4}=\dfrac{4}{\dfrac{1}{4}-4}=4:\dfrac{-15}{4}=\dfrac{-16}{15}\)
c: Để P là số nguyên thì \(4⋮x^2-4\)
=>\(x^2-4\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(x^2\in\left\{5;3;6;2;8;0\right\}\)
mà x nguyên
nên x^2=0
=>x=0(nhận)

Vì số chia là bé nhất nên số chia là: 5 + 1 = 6
Số bị chia là: 9 x 6 + 5 = 59
Đáp số: Số chia 6; số bị chia 59

Số có số hàng chục lớn hơn số hàng trăm là:
563
Chọn b.563

Để \(\dfrac{3n-5}{n-3}\) là số nguyên thì \(3n-5⋮n-3\)
=>\(3n-9+4⋮n-3\)
=>\(4⋮n-3\)
=>\(n-3\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(n\in\left\{4;2;5;1;7;-1\right\}\)

a:
ĐKXĐ: n<>1
Để \(A=\dfrac{3}{n-1}\) max thì n-1=1
=>n=2
=>\(A_{max}=\dfrac{3}{2-1}=3\)
b:
ĐKXĐ: n<>-5
\(B=\dfrac{n+9}{n+5}=\dfrac{n+5+4}{n+5}=1+\dfrac{4}{n+5}\)
Để \(B_{max}\) thì \(\dfrac{4}{n+5}\) max
=>n+5=1
=>n=-4(nhận)
Vậy: \(B_{max}=1+\dfrac{4}{-4+5}=1+4=5\)
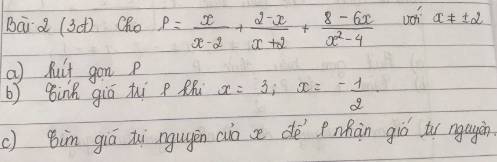
\(\dfrac{2^{2024}+2^{2023}+2^{2022}+2^{2021}}{60}=\dfrac{2^{2021}\left(2^3+2^2+2+1\right)}{60}=\dfrac{2^{2021}.15}{60}\)
\(=\dfrac{2^{2019}.2^2.15}{60}=\dfrac{2^{2019}.60}{60}=2^{2019}\)
\(\Rightarrow n=2019\)