98761

Mình nhầm

\(a.\left(4x+1\right)\left(-2x+\dfrac{1}{3}\right)=0\\ TH1:4x+1=0\\ =>4x=-1\\ =>x=-\dfrac{1}{4}\\ TH2:-2x+\dfrac{1}{3}=0\\ =>2x=\dfrac{1}{3}\\ =>x=\dfrac{1}{3}:2=\dfrac{1}{6}\\ b.\left(x-\dfrac{5}{2}\right)^3=\dfrac{-1}{8}\\ =>\left(x-\dfrac{5}{2}\right)^3=\left(-\dfrac{1}{2}\right)^2\\ =>x-\dfrac{5}{2}=-\dfrac{1}{2}\\ =>x=-\dfrac{1}{2}+\dfrac{5}{2}\\ =>x=\dfrac{4}{2}=2\\ c.\left(\dfrac{2}{5}-3x\right)^2-\dfrac{1}{5}=\dfrac{4}{25}\\ =>\left(\dfrac{2}{5}-3x\right)^2=\dfrac{4}{25}+\dfrac{1}{5}=\dfrac{9}{25}=\left(\dfrac{3}{5}\right)^2\\TH1:\dfrac{2}{5}-3x=\dfrac{3}{5}\\ =>3x=\dfrac{2}{5}-\dfrac{3}{5}=-\dfrac{1}{5}\\ =>x=\dfrac{-1}{5}:3=-\dfrac{1}{15}\\ TH2:\dfrac{2}{5}-3x=-\dfrac{3}{5}=>3x=\dfrac{2}{5}+\dfrac{3}{5}=1\\ =>x=1:3=\dfrac{1}{3}\) 

\(d.\left(\dfrac{2}{3}\right)^{x+2}+\left(\dfrac{2}{3}\right)^{x+1}=\dfrac{20}{27}\\ =>\left(\dfrac{2}{3}\right)^{x+1}\cdot\left(\dfrac{2}{3}+1\right)=\dfrac{20}{27}\\ =>\left(\dfrac{2}{3}\right)^{x+1}\cdot\dfrac{5}{3}=\dfrac{20}{27}\\ =>\left(\dfrac{2}{3}\right)^{x+1}=\dfrac{20}{27}:\dfrac{5}{3}=\dfrac{4}{9}=\left(\dfrac{2}{3}\right)^2\\ =>x+1=2\\ =>x=2-1\\ =>x=1\)

tui đang cần gấp lắm

Gọi số chia là `a`, số dư sẽ là `a - 1`

Ta có: `324 : a = 12 dư a - 1`

`=> 12a + a- 1 = 324`

`=> 13a = 325`

`=> a = 25`

Vậy số chia là `25` và số dư là `25-1=24`

Xét tổng các số trừ sau x theo dãy:

1; 2; ...; 200

- Có 200 số số hạng ( ⇒ cũng có 200 x)

- Tổng dãy trên là: (200 + 1) x 200 : 2 = 20100

Ta xét dãy: 5; 10; ...; 1000

- Khoảng cách giữa mỗi số hạng liên tiếp là: 5

- Số số hạng của dãy là: (1000 - 5) : 5 + 1 = 200  (số)

- Tổng dãy trên là: (5 + 1000) x 200 : 2 = 100500

⇒ 200x - 20100 = 100500

200x = 100500 + 20100

200x = 120600

x = 120600 : 200

x = 603

Vậy x = 603

Đặt A=5+10+15+...+1000

Tổng A có số số hạng là:

(1000-5):5+1=200(số)

Tổng A là:

(1000+5).200:2=100500

=>(2x-1)+(4x-2)+....+(400x-200)=100500

(2x+1)(1+2+...+200)=100500

Đặt B=1+2+...+200

Tổng B có số số hạng là:

(200-1):1+1=200(số)

Tổng B là:

(200+1).200:2=20100

=>(2x-1).20100=100500

=>2x-1=100500 : 20100 = 5

=>2x = 5+1

=>2x = 6

=>x = 6 : 2

=>x = 3

Số đối của 5/6 là -5/6

Số đối của \(-\dfrac{5}{2}\) là \(\dfrac{5}{2}\)

Số đối của 0,8 là -0,8

Biểu diễn:

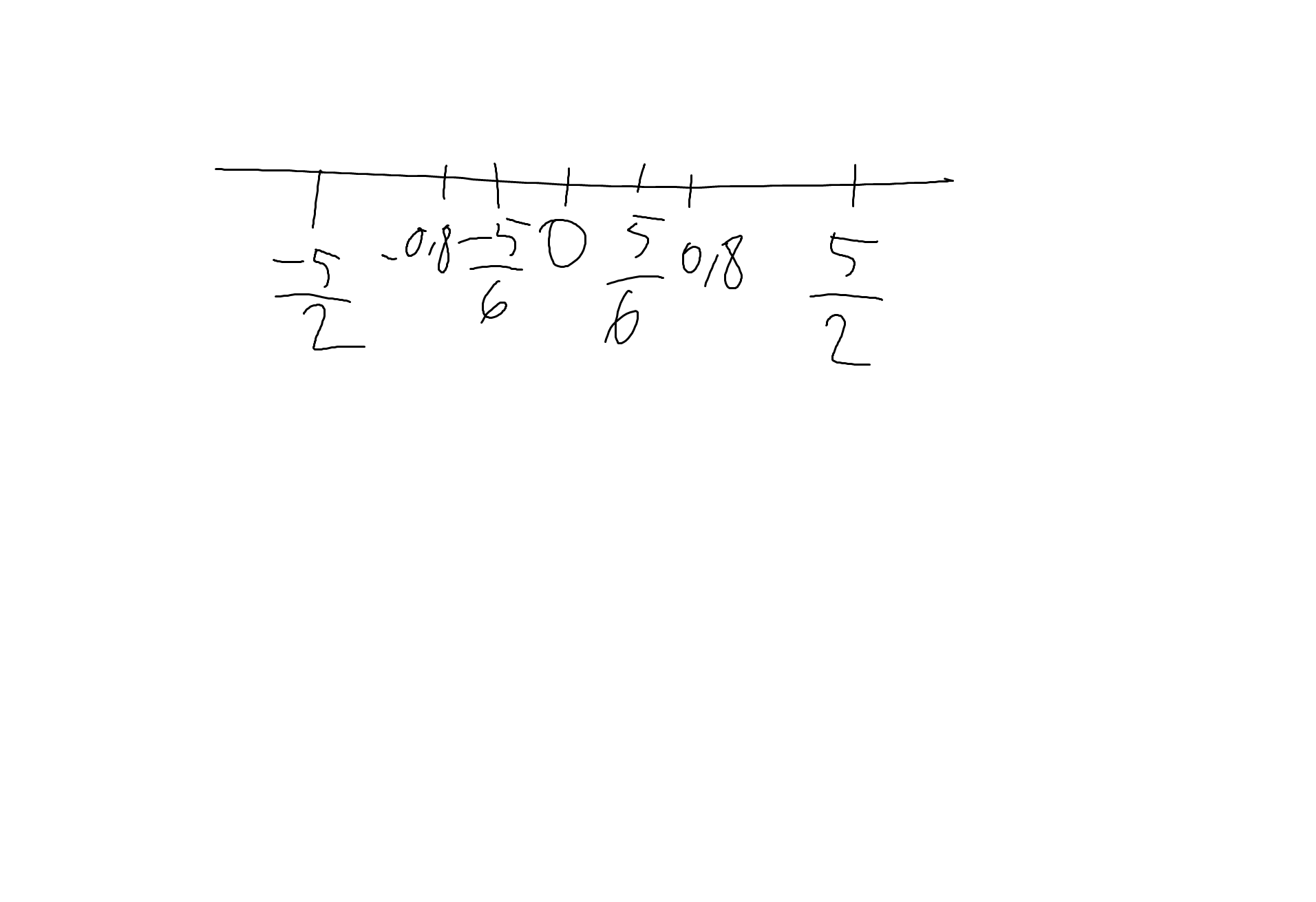
Theo đề ta có:

\(10y=2xy\left(x^2+y^2\right)+xy\left(y^2-x^2\right)\\ =2x^3y+2xy^3+xy^3-x^3y\\ =x^3y+3xy^3\\ =>y=\dfrac{x^3y+3xy^3}{10}\\ =>x=2xy\left(x^2+y^2\right)-5y=\left(2x^3y+2xy^3\right)-\dfrac{x^3y+3xy^3}{2}\\ =\dfrac{4x^3y+4xy^3-x^3y-3xy^3}{2}=\dfrac{3x^3y+xy^3}{2}\)

\(=>x-y=\dfrac{3x^3y+xy^3}{2}-\dfrac{x^3y+3xy^3}{10}=\dfrac{15x^3y+5xy^3-x^3y-3xy^3}{10}=\dfrac{14x^3y+2xy^3}{10}\\ =\dfrac{7x^3y+xy^3}{5}\)

\(a.-\dfrac{1}{3}x^2y\cdot\dfrac{3}{2}xy^3\\ =\left(-\dfrac{1}{3}\cdot\dfrac{3}{2}\right)\cdot\left(x^2\cdot x\right)\cdot\left(y\cdot y^3\right)\\ =-\dfrac{1}{2}x^3y^4\\ b.-5xy^4\left(-0,2x^2y^2\right)\\ =\left(-5\cdot-0,2\right)\cdot\left(x\cdot x^2\right)\cdot\left(y^4\cdot y^2\right)\\ =x^3y^6\\ c.\left(2x^2\right)^2\cdot\left(-3y^3\right)\\ =4x^4\cdot\left(-3y^3\right)\\ =\left(4\cdot-3\right)\cdot x^4y^3\\ =-12x^4y^3\\ d.\left(-1\dfrac{1}{2}x^2y^3\right)^2\\ =\left(-\dfrac{3}{2}x^2y^3\right)^2\\ =\dfrac{9}{4}x^4y^6\)

Khi không bán 4kg gạo cuối cùng thì ta sẽ còn lại:

17 + 4 = 21 (kg)

Vậy số gạo khi chưa bán của ngày thứ 3 là"

21 : \(\left(1-\dfrac{1}{4}\right)\) = 28 (kg)

Khi không bán 8kg vào ngày thứ 3 và dừng bán tại đó thì ta còn lại:

28 + 3 = 31 (kg)

Số gạo còn lại sau ngày thứ nhất là:

31 : \(\left(1-\dfrac{3}{5}\right)\) = 72,5 (kg)

Vậy số gạo ban đầu là:

72,5 + 5 : \(\left(1-\dfrac{1}{6}\right)\) = 93 (kg)

Đáp số: 93 kg gạo

\(16x^4+32x^3+24x^2+8x-15=0\\ \Leftrightarrow\left(16x^4-8x^3\right)+\left(40x^3-20x^2\right)+\left(44x^2-22x\right)+\left(30x-15\right)=0\\ \Leftrightarrow8x^3\left(2x-1\right)+20x^2\left(2x-1\right)+22x\left(2x-1\right)+15\left(2x-1\right)=0\\ \Leftrightarrow\left(2x-1\right)\left(8x^3+20x^2+22x+15\right)=0\\ \Leftrightarrow\left(2x-1\right)\left[\left(8x^3+12x^2\right)+\left(8x^2+12x\right)+\left(10x+15\right)\right]=0\\ \Leftrightarrow\left(2x-1\right)\left[4x^2\left(2x+3\right)+4x\left(2x+3\right)+5\left(2x+3\right)\right]\\ \Leftrightarrow\left(2x-1\right)\left(2x+3\right)\left(4x^2+4x+5\right)=0\)

Mà: \(4x^2+4x+5=\left(4x^2+4x+1\right)+4=\left(2x+1\right)^2+4>0\forall x\)

\(\Leftrightarrow\left[{}\begin{matrix}2x-1=0\\2x+3=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=-\dfrac{3}{2}\end{matrix}\right.\)

\(5^{5x-3}-2\cdot5^{21}=5^{21\cdot3}\\ =>5^{5x-3}=5^{21\cdot3}+2\cdot5^{21}\\ =>5^{5x-3}=5^{21}\cdot\left(5^3+2\right)\\ =>5^{5x-3}=5^{21}\cdot127\\ =>\dfrac{5^{5x-3}}{5^{21}}=127\\ =>5^{5x-3-21}=127\\ =>5^{5x-24}=127\\ =>5x-24=log_5127\\ =>5x=log_5127+24\\=>x=\dfrac{log_5127+24}{5}\)

5^5x-3-2 . 5²¹ = 5⁶³

5^5x-5 = 5⁶³ : 5²¹

5^5x-5 = 5⁴²

⇒ 5x - 5 = 42

5x = 42 + 5

5x = 47

x = 47 : 5

x = 9,4

Vậy x = 9,4