A B C D O 1 2 1 2 1 2

1. Xét tam giác ABD và tam giác ABC có: 

AB chung 

AD=BC ( ABCD là hình thang cân)

\(\widehat{A}=\widehat{B}\)( hai góc đối đỉnh)

=> Tam giác ABD= Tam giác ABC

2.

Ta có:  Tam giác ABD= Tam giác ABC ( theo câu 1)

=> \(\widehat{A_1}=\widehat{B_2}\)

=> Tam giác OAB cân

=> OA=OB

3. 

Ta có \(\widehat{D}=\widehat{C}\)( ABCD là hình thang cân)

=> \(\widehat{D_1}+\widehat{D_2}=\widehat{C_1}+\widehat{C_2}\)

Mà \(\widehat{D_1}=\widehat{C_1}\)( Tam giác ABD= Tam giác ABC)

=> \(\widehat{D_2}=\widehat{C_2}\)

=> Tam giác DOC cân tại O

=> DO=CO

Bài toán 8 mà sao giống toán 7 thế nhỉ?

A B C D O

a) Trong hình thang câng hai cạnh bên bằng nhau (AD = BC)

Hai góc kề ở 1 đáy bằng nhau nên theo tính chất hai đoạn thẳng song song suy ra hai góc kề ở đáy kia cũng bằng nhau.

Suy ra \(\widehat{A}=\widehat{B};\widehat{C}=\widehat{D}\)

Xét tam giác ABD và tam giác BAC có:

AD = BC (gt)

\(\widehat{A}=\widehat{B}\)

\(AB:\text{ cạnh chung }\)

\(\Rightarrow\Delta ABD=\Delta BAC\)

b) Do \(\Delta ABD=\Delta BAC\Rightarrow\widehat{DBA}=\widehat{BAC}\left(\text{hai góc tương ứng}\right)\)

\(\Rightarrow\Delta OAB\text{ cân tại O }\Rightarrow OA=OB\) (theo tính chất tam giác cân)

c) Cũng do \(\Delta ABD=\Delta BAC\Rightarrow BD=AC\Leftrightarrow OB+OD=OA+OC\)

Theo kết quả câu b ta có OA = OB suy ra OD = OC (đpcm)

Ta có

\(\left(1+\sqrt{15}\right)^2=16+2\sqrt{15}< 16+2\sqrt{16}=16+8=24\)

Ta lại có \(\sqrt{24}^2=24\)

Vậy \(1+\sqrt{15}< \sqrt{24}\)

Bài làm

Ta có: ( 1 + V15  )²  = 1 + 15 + 2 V15  = 16 + 2V15  

           V24 ² = 24 = 16 + 8

Vì V15²  = 15 < 16 = 4² 

Nên V15 < 4

=> 2V15  < 8

=> 16 + 2V15  < 24

=>  ( 1 + V15  )²  < V24 ² 

Vậy 1 + V15 < V24

# Chúc bạn học tốt #

Em tham khảo:

Câu hỏi của Thanh Triều Vương Nguyễn - Toán lớp 8 - Học toán với OnlineMath

\(\left(a+b\right).\left(b+c\right).\left(c-a\right)+\left(b+c\right).\left(c+a\right).\left(a-b\right)+\left(c+a\right).\left(a+b\right).\left(b-c\right)\)

\(=\left(a+b\right).\left[\left(b+c\right).\left(c-a\right)+\left(c+a\right).\left(a-b\right)\right]+\left(c+a\right).\left(a+b\right).\left(b-c\right)\)

\(=\left(a+b\right).\left(ac-a^2+bc-ab+a^2-ab+ac-bc\right)+\left(c+a\right).\left(a+b\right).\left(b-c\right)\)

\(=-\left(a+b\right).2a.\left(b-c\right)+\left(c+a\right).\left(a+b\right).\left(b-c\right)\)

\(=\left(a+b\right).\left(b-c\right).\left(-2a+c+a\right)=\left(a+b\right).\left(b-c\right).\left(c-a\right)\)

giai lai:

\(\left(b+c\right).\left[\left(a+b\right).\left(c-a\right)+\left(c+a\right).\left(a-b\right)\right]+\left(c+a\right).\left(a+b\right).\left(b-c\right)\)

\(=-\left(b+c\right).2a.\left(b-c\right)+\left(b-c\right).\left(ac+bc+a^2+ab\right)\)

\(=\left(b-c\right).\left(-2ab-2ac+ac+bc+a^2+ab\right)\)

\(=\left(b-c\right).\left(-ab-ac+bc+a^2\right)\)

\(=\left(b-c\right).\left(a+b\right).\left(a-c\right)\)

Có PA + PC >= AC (BĐT tam giác)

PB + PD >= BD 

=>PA + PC + PB + PD >= BD + AC

Dấu ''='' xảy ra <=> P là giao điểm của AC và BD. 

Vậy...

Ban giải thích kĩ hơn được không vậy

Ta có :

MN = AB+CD2AB+CD2

=> MN là đường trung bình của tứ giác ABCD

=> MN // AB , MN// DC

=> AB // CD

Trong tứ giác ABCD , có :

AB // CD (cmt)

=> ABCD là ht (DHNB)

học tốt

Ta có:

MN=AB+CD2MN=AB+CD2

=> MN là đường trung bình

=> MN//CD;MN//AB

=> AB//CD

=> tứ giác ABCD là hình thang

học tốt

a) Ta có: AB = AD (gt)  => A thuộc đường trung trực của BD

CB = CD (gt)   => C thuộc đường trung trực của BD.

Vậy AC là đường trung trực của BD.

b) Xét ∆ ABC và ∆ADC có AB = AD (gt)

nên ∆ ABC = ∆ADC (c.c.c)

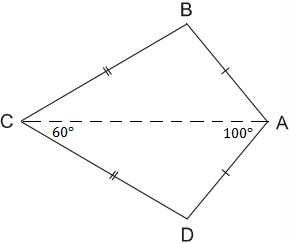
Suy ra: ⇒ˆB=ˆD

Ta có ˆB+ˆD=360⁰–(100+60)=20⁰

 Do đó ˆB=ˆD=100⁰

mban trl giúp mình câu C luôn nha ạ😭

nên đặt ở giữa 

đặt ở giữa

vì (xem ảnh)

a b c d

vậy đặt ở giữa

chúc bn

hok tốt

B) Kẻ MH vuông góc QP và NK vuông góc với QP ta có :

Ta có : MHK = NKH = 90 độ

=> MH // NK

=> Tứ giác MNKH là hình thang

Mà MHK = NKH = 90 độ

=> Tứ giác MNKH là hình thang cân

=> HMN = MNK = 90 độ

=> MNK = NKH = 90 độ

=> MN // HK 

=> MN// QP

=> MNPQ là hình thang

Mà QMN = MNP (gt)

=> MNPQ là hình thang cân(dpcm)

Ko bt tớ làm đúng ko nếu sai đừng chửi mk nhé

A B C D M I 1 2 1 2 1 2

Gọi M là giao điểm DI và AB

Ta có: AM//DC 

=> \(\widehat{M}=\widehat{D_2}\)( sole trong) (1) 

Mà \(\widehat{D_1}=\widehat{D_2}\)( DI là phân giác góc D)

=> \(\widehat{M}=\widehat{D_1}\)

=> Tam giác ADM cân 

=> ID=IM (2) 

Ta lại có: \(\widehat{I_1}=\widehat{I_2}\)( so le trong) (3)

Từ (1) , (2) => Tam giác IBM = tam giác ICD

=> BM=DC

Do  vậy: AD=AM=AB+BM=AB+DC (AD=AM vì tam giác ADM cân)

60 B A C D

+)Xét tam giác CDA  vuông tại C có: \(\widehat{CDA}=60^o\)

=> \(\widehat{CAD}=30^o\)

=> \(\widehat{BAC}=30^o\)

=> \(\widehat{BAD}=\widehat{BAC}+\widehat{CAD}=60^o=\widehat{CDA}\)

=> Hình thang ABCD cân 

=> AB=CD

Mặt khác xét tam giác BAC có: \(\widehat{BAC}=\widehat{BCA}\left(=\widehat{CAD},soletrong\right)\)

=> Tam  giác BAC cân tại B

=> BC=AB=CD

Ta lại có: Tam giác ACD vuông tại C, cạnh góc vuông CD đối diện với \(\widehat{CAD}=30^o\)

=> CD= 1/2  AD hay AD=2 CD

+) Đặt cạnh CD=x

=> AB=BC=CD=x và AD=2CD=2x

Chu vi của hình thang là:

AB+BC+CD+AD=50

<=> x+x+x+2x=50

<=> 5x=50

<=> x=10

Vậy các cạnh của hình thang : AB=BC=CD=10 cm, AD= 20 cm