\(\dfrac{x-2}{x+1}\)=\(\dfrac{x^2-3x+2}{x^2-1}\)với x ≠ 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bạn cần làm gì với đa thức này bạn cần ghi chú rõ ra.
em cần viết rõ yêu cầu đề bài nhé, và nên gõ công thức trực quan để đề rõ ràng hơn


1 con gà có 2 chân
1 con chó có 4 chân
Giả sử 36 con đều là chó
36 con chó có số chân là: 4 x 36 = 144 (chân)
Số chân tăng thêm là: 144 - 100 = 44 (chân)
1 con gà ít hơn 1 con chó số chân là: 4 - 2 = 2 (chân)
Có số con gà là : 44 : 2 = 22 (con)
Có số con chó là: 36 - 22 = 14 (con)
đ/s:....
Gọi số gà là : x
theo bài ra ta có hệ phương trình
2x+4(36-x)=100
2x+144-4x=100
-2x=100-144
-2x=-44
x=-44:-2
x=22
Suy ra có 22 con gà
Số chó là :
36-22=14(con)
Vậy....

\(\dfrac{1}{x}+\dfrac{1}{x+2}+\dfrac{x-2}{x^2+2x}\\ =\dfrac{1}{x}+\dfrac{1}{x+2}+\dfrac{x-2}{x.\left(x+2\right)}\\ =\dfrac{x+2}{x.\left(x+2\right)}+\dfrac{x}{x.\left(x+2\right)}+\dfrac{x-2}{x.\left(x+2\right)}\\ =\dfrac{x+2+x+x-2}{x.\left(x+2\right)}\\ =\dfrac{3x}{x.\left(x+2\right)}\\ =\dfrac{3}{x+2}\)
Đầu tiên, em tìm ĐKXĐ, sau đó biến đổi vế trái:
VT = $\dfrac{1}{x}+\dfrac{1}{x+2}+\dfrac{x-2}{x^2+2x}=\dfrac{1}{x}+\dfrac{1}{x+2}+\dfrac{x-2}{x.\left(x+2\right)}$
$=\dfrac{x+2}{x.\left(x+2\right)}+\dfrac{x}{x.\left(x+2\right)}+\dfrac{x-2}{x.\left(x+2\right)} =\dfrac{x+2+x+x-2}{x.\left(x+2\right)}$
$=\dfrac{3x}{x.\left(x+2\right)}=\dfrac{3}{x+2}$ = VP.

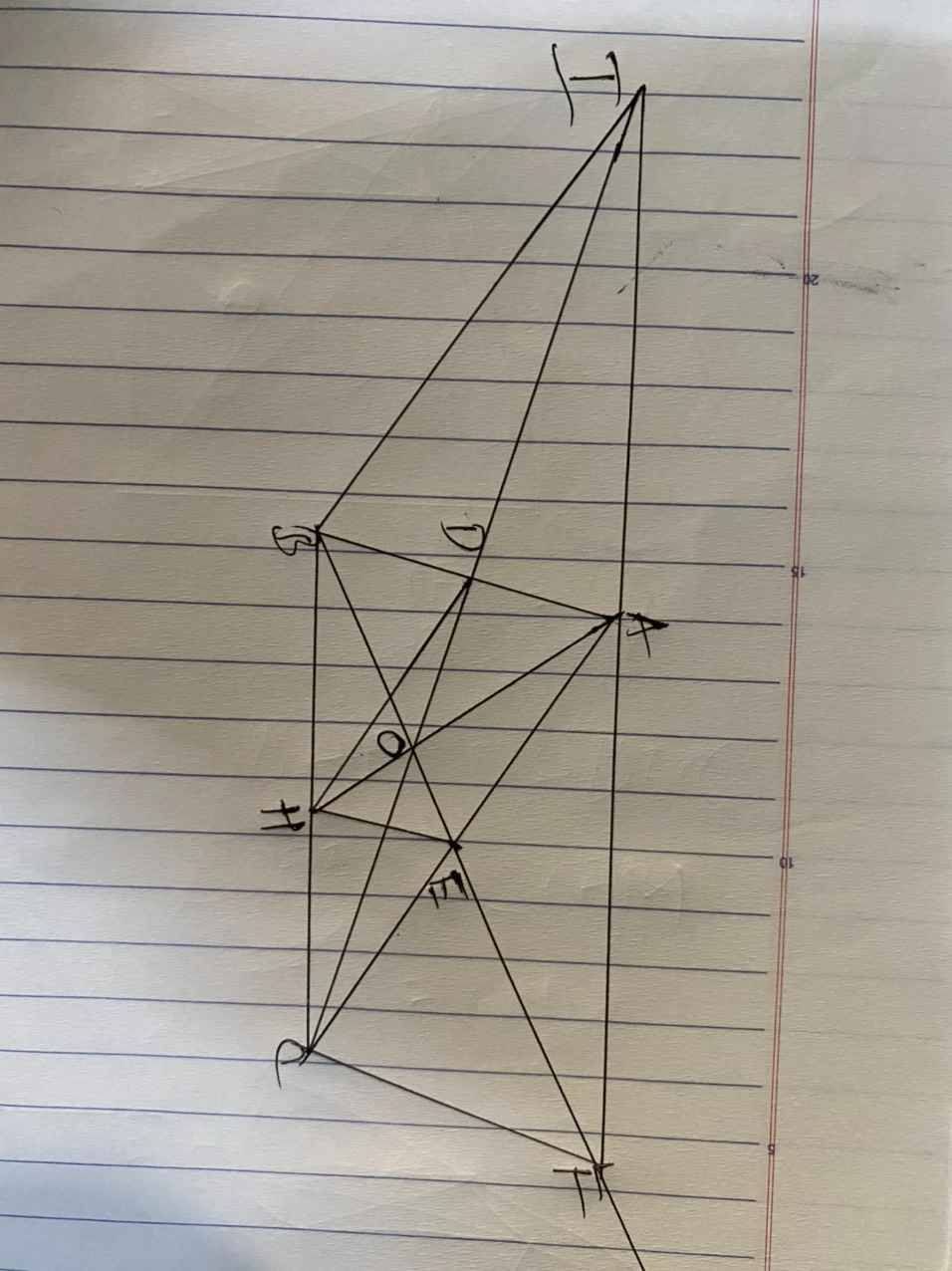
a) vì I đối xứng với C qua D → ID= DC hay D là trung điểm IC
xét tứ giác ACBI có 2 dg chéo IC và AB cắt nhau tại trung điểm D mỗi dg
→ ACBI là hbh
⇒ BI //=AC
và IA//=BC(1)
b) chứng minh tương tự như trên ta có ABCF là hbh ( do có 2 dg chéo AC và BF cắt nhau tại trung điểm E mỗi dg)
⇒ AF//=BC (2)
từ (1)(2) ⇒ I, A, F thẳng hàng và FI//BC
BCFI là hình thang
c)ADHE là hbh
do D, E là trung điểm AB, AC nên O là giao điểm 3 dg trung tuyến ⇒ AH là trung tuyến ứng với cạnh BC ⇒ H là trung điểm BC
áp dụng tc dg trung bình sẽ có DH // và =1/2 AC = AE = EC
EH // và = 1/2 AB = AD= DB
tứ giac ADHE có 2 AE//=DH và AD//=EH
⇒ ADHE là hbh
d) dk la hình thoi khi hbh ADHE có 2 cạnh kề = nhau là AD = AE
vậy khi △ABC cân thi ADHE là h thoi

\(a^2-6a-7\\ =a^2-7a+a-7\\ =a\left(a-7\right)+\left(a-7\right)\\ =\left(a+1\right)\left(a-7\right)\)
\(a^2-6a-7\)
\(=a^2+a-7a-7\)
\(=a\left(a+1\right)-7\left(a+1\right)\)
\(=\left(a+1\right)\left(a-7\right)\)
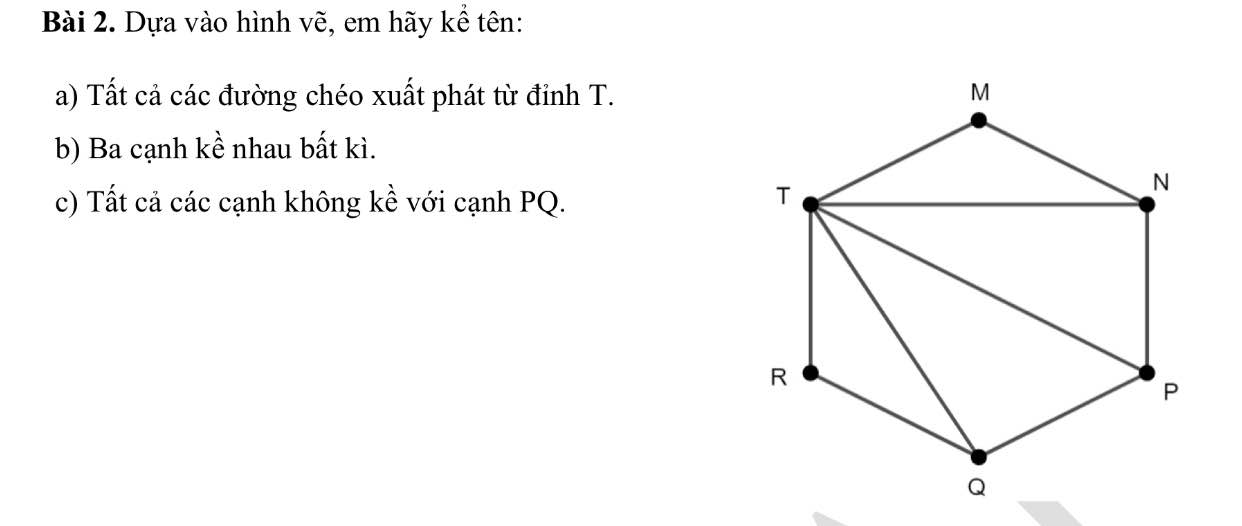

x^2-3x+2/x^2-1
=x^2-x-2x+2/(x+1).(x-1)
=x(x-1)-2(x-1)/(x+1)(x-1)
=(x-2)(x-1)/(x+1)(x-1)
=(x-2)/(x+1)
\(\dfrac{x-2}{x+1}=\dfrac{x^2-3x+2}{x^2-1}\)
\(\dfrac{x-2}{x+1}=\dfrac{\left(x^2-2x+1\right)-\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}\)
\(\dfrac{x-2}{x+1}=\dfrac{\left(x-1\right)^2-\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}\)
\(\dfrac{x-2}{x+1}=\dfrac{\left(x-1\right)\left(x-1-1\right)}{\left(x-1\right)\left(x+1\right)}\)
\(\dfrac{x-2}{x+1}=\dfrac{x}{x+1}\)
\(\Leftrightarrow x\left(x+1\right)=\left(x-2\right)\left(x+1\right)\)
\(\Leftrightarrow x^2+x=x^2+x-2x+1\)
\(\Leftrightarrow x^2+x-x^2+x+1=0\)
\(\Leftrightarrow2x=1\)
\(\Leftrightarrow x=\dfrac{1}{2}\left(tm\right)\)
Vậy ...