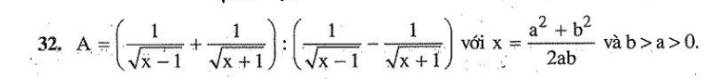Cho BC là dây cung cố định trên đường tròn (O), (BC không là đường
kính), A là điểm di động trên cung lớn BC, (A không trùng B, C). Gọi AD, BE, CF là các
đường cao của tam giác ABC; EF cắt BC tại P. Qua điểm D vẽ đường thẳng song song với
EF cắt AC tại Q và cắt AB tại R.
a) Chứng minh tứ giác BQCR là tứ giác nội tiếp.
b) Gọi M là trung điểm cạnh BC. Chứng minh rằng hai tam giác EPM và DEM là hai
tam giác đồng dạng.
c) Chứng minh rằng đường tròn ngoại tiếp tam giác PQR luôn đi qua một điểm cố định.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Từ \(x^3+y^3+z^3=-3\)
\(\Leftrightarrow2x^3+2y^3+2z^3=-6\)
\(\Leftrightarrow2x^3+2y^3+2z^3=-3\left(x^2y+y^2z+z^2x\right)-3\left(xy^2+yz^2+zx^2\right)\)
\(\Leftrightarrow\left(x^3+3x^2y+3xy^2+y^3\right)+\left(y^3+3y^2z+3yz^2+z^3\right)+\left(z^3+3z^2x+3zx^2+x^3\right)=0\)
\(\Leftrightarrow\left(x+y\right)^3+\left(y+z\right)^3+\left(z+x\right)^3=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+y+y+z+z+x=0\\x+y=y+z=z+x\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x+y+z=0\\x=y=z\end{matrix}\right.\)
Xét TH \(x=y=z\), thay vào pt thứ 3 của hệ, ta có \(3x^3=-3\Leftrightarrow x=-1\) \(\Rightarrow\left(x;y;z\right)=\left(-1;-1;-1\right)\). Thử lại vào 2 pt đầu, ta thấy rõ ràng không thỏa mãn.
Xét TH \(x+y+z=0\), ta sẽ có \(x^3+y^3+z^3=3xyz\) \(\Rightarrow xyz=-1\)
Thay vào pt đầu tiên của hệ, thu được \(x^2y+y^2z+z^2x=-xyz\) \(\Leftrightarrow x^2y+y^2z+z^2x+xyz=0\). Tương tự, ta có \(xy^2+yz^2+zx^2+xyz=0\). Cộng theo vế 2 pt này, ta được \(\left(x+y\right)\left(y+z\right)\left(z+x\right)=0\) \(\Leftrightarrow\left[{}\begin{matrix}x+y=0\\y+z=0\\z+x=0\end{matrix}\right.\). Ta xét TH \(x+y=0\). Do \(x+y+z=0\) nên \(z=0\) và \(x=-y\), không thỏa mãn pt thứ 3. Tương tự với 2 trường hợp còn lại.
Vậy hpt đã cho vô nghiệm.
Nhớ tick nha
⎧⎪⎨⎪⎩3x2+xz−yz+y2=2(1)y2+xy−yz+z2=0(2)x2−xy−xz−z2=2(3){3�2+��−��+�2=2(1)�2+��−��+�2=0(2)�2−��−��−�2=2(3)
Lấy (2) cộng (3) ta được
x2+y2−yz−zx=2�2+�2−��−��=2 (4)
Lấy (1) - (4) ta được
2x(x+z)=02�(�+�)=0
⇔[x=0x=−z⇔[�=0�=−�
Xét 2 TH rồi thay vào tìm được y và z

A =\(\left(\dfrac{1}{\sqrt{x-1}}+\dfrac{1}{\sqrt{x+1}}\right):\left(\dfrac{1}{\sqrt{x-1}}-\dfrac{1}{\sqrt{x+1}}\right)\)
\(=\dfrac{\sqrt{x+1}+\sqrt{x-1}}{\sqrt{x^2-1}}.\dfrac{\sqrt{x^2-1}}{\sqrt{x+1}-\sqrt{x-1}}\)
\(=\left(\sqrt{x+1}+\sqrt{x-1}\right).\dfrac{1}{\sqrt{x+1}-\sqrt{x-1}}\)
\(=\left(\sqrt{x+1}+\sqrt{x-1}\right).\dfrac{\sqrt{x+1}+\sqrt{x-1}}{x+1-\left(x-1\right)}\)
\(=\dfrac{\left(\sqrt{x+1}+\sqrt{x-1}\right)^2}{2}\)
\(=\dfrac{x+1+x-1+2\sqrt{x^2-1}}{2}\)
\(=x+\sqrt{x^2-1}=\dfrac{a^2+b^2}{2ab}+\sqrt{\left(\dfrac{a^2+b^2}{2ab}\right)^2-1}\)
\(=\dfrac{a^2+b^2}{2ab}+\sqrt{\dfrac{a^4+b^4+2a^2b^2}{4a^2b^2}-\dfrac{4a^2b^2}{4a^2b^2}}\)
\(=\dfrac{a^2+b^2}{2ab}+\sqrt{\dfrac{\left(a^2-b^2\right)^2}{4a^2b^2}}\)
\(=\dfrac{a^2+b^2}{2ab}+\dfrac{b^2-a^2}{2ab}\) (do b > a > 0 nên b2 - a2 > 0)
\(=\dfrac{2b^2}{2ab}=\dfrac{b}{a}\)

Các điều kiện xác định hợp lại sẽ là \(\left\{{}\begin{matrix}2\le x\le4\\0\le y\le2\end{matrix}\right.\)
Ta có \(8\sqrt{xy-2y}-8y+4\) \(=8\sqrt{y\left(x-2\right)}-8y+4\) \(\le4\left(y+x-2\right)-8y+4\) (BĐT AM-GM) \(=4\left(x-y\right)-4\)
Do vậy, \(\left(x-y\right)^2=8\sqrt{xy-2y}-8y+4\le4\left(x-y\right)-4\) \(\Leftrightarrow\left(x-y\right)^2-4\left(x-y\right)+4\le0\) \(\Leftrightarrow\left(x-y-2\right)^2\le0\) \(\Leftrightarrow x-y-2=0\) \(\Leftrightarrow y=x-2\), điều này cũng thỏa mãn ĐTXR của BĐT \(8\sqrt{y\left(x-2\right)}=4\left(y+x-2\right)\). Do đó, pt đầu tiên của hệ \(\Leftrightarrow y=x-2\) hay \(x=y+2\)
Thay vào pt thứ 2 của hệ, ta có
\(2\sqrt{2y-y^2}\left(\sqrt{4-2y}-2\sqrt{2y}+1\right)=4y+5\sqrt{2-y}-10\sqrt{y}\)
\(\Leftrightarrow\left(4-2y\right)\sqrt{2y}-4y\sqrt{4-2y}+2\sqrt{y\left(2-y\right)}=4y+5\sqrt{2-y}-10\sqrt{y}\)
Mình mới làm được đến đây thôi. Mình phải đi ngủ rồi, thế nên mai mình suy nghĩ tiếp nhé.

A = \(\dfrac{x+3}{\sqrt{x}+1}\); \(x\) = 9 - 4\(\sqrt{2}\)
Thay \(x\) = 9 - 4\(\sqrt{2}\) vào biểu thức A = \(\dfrac{x+3}{\sqrt{x}+1}\) ta có:
A = \(\dfrac{9-4\sqrt{2}+3}{\sqrt{9-4\sqrt{2}}+1}\) = \(\dfrac{12-4\sqrt{2}}{\sqrt{8-4\sqrt{2}+1}+1}\)
A = \(\dfrac{12-4\sqrt{2}}{\sqrt{\left(2\sqrt{2}-1\right)^2}+1}\) = \(\dfrac{12-4\sqrt{2}}{2\sqrt{2}-1+1}\)
A = \(\dfrac{12-4\sqrt{2}}{2\sqrt{2}}\) = \(\dfrac{2\sqrt{2}\left(3\sqrt{2}-2\right)}{2\sqrt{2}}\)
A = 3\(\sqrt{2}\) - 2

gọi số thỏa mãn đề bài là \(x^2\) ( \(x\) \(\in\) N) Theo bài ra ta có:
236 ≤ \(x^2\) ≤ 335 ⇒ 15,3 \(\le\) \(x\) \(\le\) 18,3
⇒ \(x\) \(\in\) { 16; 17}
Vậy số chính phương có trong dãy số 236 đến 335 là:
162 và 172

Bạn nên có bài cụ thể thì mọi người sẽ hướng dẫn được. Tách thì cũng phải dựa vào điều kiện.

Gọi P là 1 giá trị của biểu thức trên.
Ta có \(P=\dfrac{ax+b}{x^2+1}\Leftrightarrow\left(x^2+1\right)P-\left(ax+b\right)=0\)
\(\Leftrightarrow Px^2-ax+P-b=0\left(1\right)\)
Vì giá trị nhỏ nhất và giá trị lớn nhất đều khác 0, nên \(P\ne0\)
Để P tồn tại thì phương trình (1) phải có nghiệm hay \(\Delta_{\left(1\right)}\ge0\)
\(\Leftrightarrow\left(-a\right)^2-4P\left(P-b\right)\ge0\Leftrightarrow4P^2-4Pb-a^2\le0\left(2\right)\)
Gọi \(P_1,P_2\left(P_1< P_2\right)\) là 2 nghiệm của phương trình \(4P^2-4Pb-a^2=0\left(3\right)\)
Khi đó phương trình (2) có nghiệm \(P_1\le P\le P_2\) nên P đạt Min tại giá trị \(P_1\), đạt Max tại giá trị \(P_2\).
Do đó, yêu cầu của bài toán chỉ thỏa mãn khi và chỉ khi phương trình (3) có 2 nghiệm -1 và 4, tức: \(\left\{{}\begin{matrix}4+4b-a^2=0\\64-16b-a^2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=3\\a^2=16\end{matrix}\right.\) hay \(\left\{{}\begin{matrix}b=3\\a=\pm4\end{matrix}\right.\)
Vậy \(\left\{{}\begin{matrix}a=4\\b=3\end{matrix}\right.\) hoặc \(\left\{{}\begin{matrix}a=-4\\b=3\end{matrix}\right.\)