
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(n_{H_2}\)= \(\dfrac{0,756}{24,79}\) = 0,0305 mol
PTHH:
Mg + 2HCl → MgCl2 + H2
Al + 3HCl → AlCl3 + \(\dfrac{3}{2}\)H2
Gọi số mol của Mg và Al lần lượt là x và y.
Ta có hệ phương trình
\(\left\{{}\begin{matrix}24x+27y=0,615\\x+1,5y=0,0305\end{matrix}\right.\)↔\(\left\{{}\begin{matrix}x=0,011\\y=0,013\end{matrix}\right.\)
⇒ mMg = 0,11 . 24 = 0,264 gam
⇒ %Mg = \(\dfrac{0,264}{0,615}\) . 100 = 43%


a: Để (d) có hệ số góc bằng -2 thì m-1=-2
=>m=-1
b: Thay x=-3 và y=0 vào (d), ta được:
\(-3\left(m-1\right)+2m=0\)
=>-3m+3+2m=0
=>3-m=0
=>m=3
c: Thay x=0 và y=2 vào (d), ta được:
0(m-1)+2m=2
=>2m=2
=>m=1
d: Để (d)//(d1) thì \(\left\{{}\begin{matrix}m-1=-3\\2m\ne4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m=-2\\m\ne2\end{matrix}\right.\)
=>m=-2
a) Tìm 𝑚m để 𝑑d có hệ số góc bằng -2.
Hệ số góc của đường thẳng 𝑑d là 𝑚−1m−1. Để 𝑑d có hệ số góc bằng -2, ta giải phương trình: 𝑚−1=−2
m−1=−2 𝑚=−2+1
\(\Rightarrow\)m=−2+1 𝑚=−1
\(\Rightarrow\)m=−1
b) Tìm 𝑚m để 𝑑d cắt trục hoành tại điểm có hoành độ bằng -3.
Khi 𝑑d cắt trục hoành, 𝑦=0y=0, từ đó: (𝑚−1)𝑥+2𝑚=0
(m−1)x+2m=0 (𝑚−1)(−3)+2𝑚=0
\(\Rightarrow\)(m−1)(−3)+2m=0 3(𝑚−1)+2𝑚=0
\(\Rightarrow\)3(m−1)+2m=0 3𝑚−3+2𝑚=0
\(\Rightarrow\)3m−3+2m=0 5𝑚−3=0
\(\Rightarrow\)5m−3=0 5𝑚=3
\(\Rightarrow\)5m=3 𝑚=35
\(\Rightarrow\)m= 3/5
c) Tìm 𝑚m để 𝑑d cắt trục tung tại điểm có tung độ bằng 2.
Khi 𝑑d cắt trục tung, 𝑥=0x=0, khi đó: (𝑚−1)⋅0+2𝑚=2
(m−1)⋅0+2m=2
\(\Rightarrow\)2𝑚=2\(\Rightarrow\)2m=2 𝑚=1
\(\Rightarrow\)m=1
d) Tìm 𝑚m để 𝑑d song song với đường thẳng 𝑑1d
: 𝑦=−3𝑥+4y=−3x+4.
Đường thẳng 𝑑d sẽ song song với 𝑑1d nếu hệ số góc của 𝑑d bằng hệ số góc của 𝑑1d: dđ𝑚−1=−3
\(\Rightarrow\) m−1=−3 𝑚=−3+1
\(\Rightarrow\)m=−3+1 𝑚=−2
\(\Rightarrow\)m=−2
Kết luận:a) 𝑚=−1m = -1
b) 𝑚=35m = 3/5
c) 𝑚=1m = 1
d) 𝑚=−2m = −2

a: Xét ΔAHB vuông tại H và ΔCHA vuông tại H có
\(\widehat{HAB}=\widehat{HCA}\left(=90^0-\widehat{ABC}\right)\)
Do đó: ΔAHB~ΔCHA
b: Ta có: \(\widehat{BAD}+\widehat{CAD}=\widehat{BAC}=90^0\)
\(\widehat{BDA}+\widehat{DAH}=90^0\)(ΔDAH vuông tại H)
mà \(\widehat{CAD}=\widehat{DAH}\)
nên \(\widehat{BAD}=\widehat{BDA}\)
=>ΔBAD cân tại B
ΔBAD cân tại B
mà BF là đường phân giác
nên BF\(\perp\)AD tại F
Xét ΔEFA vuông tại F và ΔEHB vuông tại H có
\(\widehat{FEA}=\widehat{HEB}\)(hai góc đối đỉnh)
Do đó: ΔEFA~ΔEHB
=>\(\dfrac{EF}{EH}=\dfrac{EA}{EB}\)
=>\(EF\cdot EB=EA\cdot EH\)
c: Xét ΔBAK và ΔBDK có
BA=BD
\(\widehat{ABK}=\widehat{DBK}\)
BK chung
Do đó: ΔBAK=ΔBDK
=>\(\widehat{BAK}=\widehat{BDK}\)
=>\(\widehat{BDK}=90^0\)
=>KD\(\perp\)BC
=>KD//AH
d: Xét ΔBKD có EH//KD
nên \(\dfrac{EH}{KD}=\dfrac{BH}{BD}\)
=>\(\dfrac{EH}{KD}=\dfrac{BH}{BA}\)
Xét ΔBHA vuông tại H và ΔBAC vuông tại A có
\(\widehat{HBA}\) chung
Do đó: ΔBHA~ΔBAC
=>\(\dfrac{BH}{BA}=\dfrac{BA}{BC}\)
=>\(\dfrac{EH}{KD}=\dfrac{BA}{BC}\)
=>\(\dfrac{EH}{BA}=\dfrac{KD}{BC}\)

Lời giải:
Giả sử theo kế hoạch tổ sản xuất trong $n$ ngày.
Số sản phẩm theo kế hoạch: $50n$ (sản phẩm)
Số sản phẩm thực tế: $57(n-1)$ (sản phẩm)
Theo bài ra ta có:
$57(n-1)=50n+13$
$\Leftrightarrow 7n=70$
$\Leftrightarrow n=10$
Theo kế hoạch tổ phải sản xuất số sản phẩm là:
$50n=50.10=500$ (sản phẩm)
Gọi số sp tổ phải sản xuất theo kế hoạch là: x(sản phẩm) ĐK:x>13
\(\Rightarrow\)Thời gian dự định làm là: \(\dfrac{x}{50}\)(ngày)
Thời gian thực tế là: \(\dfrac{x+13}{57}\)(ngày)
Theo bài ra ta có pt:
\(\dfrac{x}{50}\)-\(\dfrac{x+13}{57}\)=1
\(\Leftrightarrow\)2850(\(\dfrac{x}{50}\)-\(\dfrac{x+13}{57}\))=2850
\(\Leftrightarrow\)\(57x-50x-650=2850\)
\(\Leftrightarrow\)\(7x=3500\)
\(\Leftrightarrow\)\(x=500\)
Vậy ....

- \(\dfrac{2}{5}\)\(x^2\)y.2\(xy^3\).\(\dfrac{1}{4}\)yz
= (-\(\dfrac{2}{5}\).2.\(\dfrac{1}{4}\)).(\(x^2\).\(x\)).(y.y3.y).z
= - \(\dfrac{1}{5}\)\(x^3\).y5.z
\(-\dfrac{2}{5}x^2y\cdot2xy^3\cdot\dfrac{1}{4}yz\)
\(=\left(-\dfrac{2}{5}\cdot2\cdot\dfrac{1}{4}\right)\cdot\left(x^2\cdot x\right)\cdot\left(y\cdot y^3\cdot y\right)\cdot z\)
\(=-\dfrac{1}{5}x^3y^5z\)

program XoaChuSoLonNhat;
var
s: string;
i, j, k, vitri: integer;
soLonNhat: longint;
function ChuanHoa(s: string): string;
var
i, j: integer;
begin
for i := 1 to Length(s) do
if s[i] = '0' then
Delete(s, i, 1);
for i := 1 to Length(s) do
if s[i] = '-' then
Delete(s, i, 1);
if s[1] = '+' then
Delete(s, 1, 1);
end;
function TimViTriLonNhat(s: string): integer;
var
i, j: integer;
begin
vitri := 1;
for i := 2 to Length(s) do
if s[i] > s[vitri] then
vitri := i;
end;
function XoaChuSo(s: string; vitri: integer): string;
var
i: integer;
begin
Delete(s, vitri, 1);
for i := vitri to Length(s) do
Inc(s[i]);
end;
function ChuyenSangSo(s: string): longint;
var
i, so: integer;
begin
so := 0;
for i := 1 to Length(s) do
so := so * 10 + Ord(s[i]) - Ord('0');
if s[1] = '-' then
so := -so;
end;
begin
Writeln('Nhap xau: ');
Readln(s);
s := ChuanHoa(s);
vitri := TimViTriLonNhat(s);
soLonNhat := ChuyenSangSo(XoaChuSo(s, vitri));
Writeln('So lon nhat sau khi xoa 1 chu so: ', soLonNhat);
end
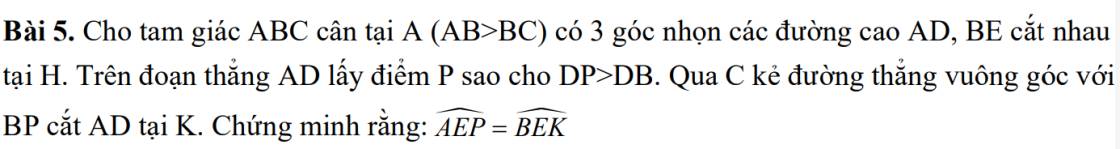

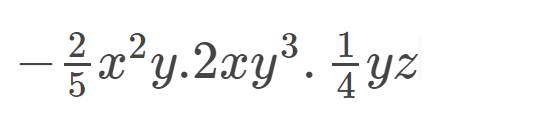
a: Xét ΔABC có
D,E lần lượt là trung điểm của AB,AC
=>DE là đường trung bình của ΔABC
=>DE//BC và BC=2DE
b: Xét ΔAFB có
D là trung điểm của AB
DI//FB
Do đó: I là trung điểm của AF
Xét ΔAFB có ID//FB
nên \(\dfrac{ID}{FB}=\dfrac{AD}{AB}=\dfrac{1}{2}\)
Xét ΔAFC có IE//FC
nên \(\dfrac{IE}{FC}=\dfrac{AE}{AC}=\dfrac{1}{2}\)
Do đó: \(\dfrac{ID}{FB}=\dfrac{IE}{FC}\)
mà ID=IE(I là trung điểm của DE)
nên FB=FC
=>F là trung điểm của BC
Xét tứ giác AEFD có
I là trung điểm chung của AF và ED
=>AEFD là hình bình hành
Hình bình hành AEFD có \(\widehat{EAD}=90^0\)
nên AEFD là hình chữ nhật
c: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
\(DE=\dfrac{1}{2}BC=\dfrac{1}{2}\cdot10=5\left(cm\right)\)
I là trung điêm của DE
=>ID=IE=DE/2=2,5(cm)
=>AI=ED/2=2,5(cm)
ΔABC vuông tại A
mà AF là đường trung tuyến
nên AF=BC/2=5(cm)
Xét ΔABC có
BE,AF là các đường trung tuyến
BE cắt AF tại K
Do đó: K là trọng tâm của ΔABC
=>\(AK=\dfrac{2}{3}AF=\dfrac{2}{3}\cdot5=\dfrac{10}{3}\left(cm\right)\)
AI+IK=AK
=>\(IK+2,5=\dfrac{10}{3}\)
=>\(IK=\dfrac{10}{3}-\dfrac{5}{2}=\dfrac{20}{6}-\dfrac{15}{6}=\dfrac{5}{6}\left(cm\right)\)