Lời giải:

a. Bạn tự vẽ

b. Gọi ptđt $(D)$ là $y=ax+b$. Vì $A\in (D)$ nên:

$y_A=ax_A+b\Leftrightarrow -3=a+b(1)$

$(D)$ tiếp xúc với $(P)$
$\Leftrightarrow$ phương trình hoành độ giao điểm $x^2-ax-b=0$ có nghiệm kép 

$\Leftrightarrow \Delta=a^2+4b=0(2)$

Từ $(1); (2)\Rightarrow a=6$ hoặc $a=-2$
Nếu $a=6$ thì $b=-3-a=-9$. 

Nếu $a=-2$ thì $b=-3-a=-3-(-2)=-1$
Vậy ptđt $(D)$ là $y=6x-9$ hoặc $y=-2x-1$

c. 

PT hoành độ giao điểm của $(d)$ và $(P)$:

$x^2-(2-m)x-(m-1)=0$

Để $(P)$ và $(d)$ cắt nhau tại 2 điểm pb thì:

$\Delta=(2-m)^2+4(m-1)>0\Leftrightarrow m^2>0\Leftrightarrow m\neq 0$

Áp dụng định lý Viet:

$x_1+x_2=2-m$

$x_1x_2=-(m-1)=1-m$

$\Rightarrow x_1x_2-x_1-x_2=-1$

$\Leftrightarrow x_1x_2-x_1-x_2+1=0$

$\Leftrightarrow (x_1-1)(x_2-1)=0$

$\Leftrightarrow x_1=1$ hoặc $x_2=1$

Nếu $x_1=1$

$x_2^3-2x_1=64$

$\Leftrightarrow x_2^3-2=64\Leftrightarrow x_2^3=66$

$\Leftrightarrow x_2=\sqrt[3]{66}$
$2-m=x_1+x_2=1+\sqrt[3]{66}$

$\Leftrightarrow m=1-\sqrt[3]{66}$

Nếu $x_2=1$

$x_2^3-2x_1=64$

$\Leftrightarrow 1-2x_1=64$

$\Leftrightarrow x_1=\frac{-63}{2}$

$2-m=x_1+x_2=\frac{-63}{2}+1=\frac{-61}{2}$

$\Leftrightarrow m=\frac{65}{2}$

Ta thấy \(x>0\) nên ta có thể suy ra \(\sqrt{x}=\sqrt{4-2\sqrt{3}}\) \(=\sqrt{3-2\sqrt{3}+1}\) \(=\sqrt{\left(\sqrt{3}\right)^2-2\sqrt{3}+1}\) \(=\sqrt{\left(\sqrt{3}-1\right)^2}\) \(=\sqrt{3}-1\) (do \(\sqrt{3}-1>0\))

Từ đó \(Q=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\) \(=\dfrac{\sqrt{3}-1+1}{\sqrt{3}-1-3}\) \(=\dfrac{\sqrt{3}}{\sqrt{3}-4}\) \(=\dfrac{\sqrt{3}\left(\sqrt{3}+4\right)}{\left(\sqrt{3}-4\right)\left(\sqrt{3}+4\right)}\) \(=\dfrac{3+4\sqrt{3}}{\left(\sqrt{3}\right)^2-4^2}\) \(=-\dfrac{3+4\sqrt{3}}{13}\)

Ta có : \(x\text{=}4-2\sqrt{3}\)

\(\Rightarrow x=3-2\sqrt{3}+1\)

\(\Rightarrow x=\left(\sqrt{3}-1\right)^2\)

\(\Rightarrow\sqrt{x}=\sqrt{\left(\sqrt{3}-1\right)^2}\text{=}\sqrt{3}-1\)

Do đó :

\(Q\text{=}\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)

\(Q\text{=}\dfrac{\sqrt{3}-1+1}{\sqrt{3}-1-3}\)

\(Q\text{=}\dfrac{\sqrt{3}}{\sqrt{3}-4}\)

Chắc đến đây thôi nhỉ .

Pattern 2

0 Don't forget to write a sick note when you're sick

1 Don't forget to brush your teeth regularly

2 Don't forget to wash vegetables carefully

3 Remember to take morning exercises regulary

4 Don't forget not to eat too much candy

5 Don't forget to iron and wash your own clothes

---

Pattern 3

0 I had a stomachache last night

1 My tooth hurts

2 Her stomach hurt yesterday

3 His head hurt last night

4 Minh's tooth hurts

5 Lan had a headache yesterday

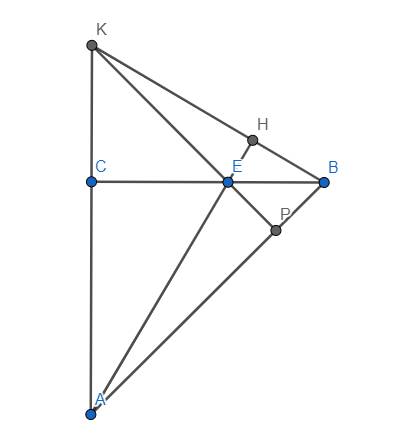
 Do \(CA=CB=a\) nên \(BE.BC+AC.AK=a\left(AK+BE\right)\) 

 Ta chứng minh \(AK+BE\) không đổi. Thật vậy, gọi P là giao điểm của KE và AB. Quan sát thấy E là trực tâm tam giác ABK \(\Rightarrow KP\perp AP\) tại P. Lại có \(\widehat{KAP}=45^o\) nên suy ra \(\widehat{AKP}=45^o\). Từ đó suy ta tam giác CEK cân tại C hay \(CE=CK\). 

 Từ đó \(AK+BE=AC+CK+BC-CE=2a\). Vậy \(BE.BC+AC.AK=2a^2\) không đổi (đpcm)

VI )

1) This shirt is too small for me to wear.
=> This shirt isn’t big enough for me to wear
2) That suitcase isn’t big enough to hold all my clothes.
=> That suitcase is so small that it can't hold all my clothes
3) I get home too late to watch the show.
=> I don’t get home early enough to watch the show
4) This computer isn’t fast enough for us to handle the job.
=> It is such a slow computer that we can't handle the job
5) I was too sick to do my homework.
=> I was so sick that I can't do my homework
6) I am too poor to buy a car.
=> I am not poor enough to buy a car
7) The weather was too bad for her to go for a picnic.
=> The weather was so bad that she couldn't go for a picnic
8) Tom is too young to see the horror film.
=> Tom is so young that he can't see the horror film
9) He drank so much coffee that he could get to sleep.
=> He drank such a lot of coffee that he could get to sleep
10) The door was too heavy for the child to push on.
=> It was such a heavy door that the child couldn't push on.

VII

She is a good cook

He is a slow cyclist

My uncle is a good English teacher

Many students were involved in the campaign against air pollution 

He is a careful typist

He is a good guitar player

He was severely punished from the master

His father takes up fishing

Rita is proud of her family tradition

These children can run quickly

Ta có : \(S_{ABC}=\dfrac{AH.BC}{2}\)

Kẻ đường cao từ B xuống AC tại E do đó :

\(S_{ABC}=\dfrac{BE.AC}{2}\)

mà \(BE< AB\) ( AB là cạnh huyền trong tam giác ABE )

Do đó :

\(\dfrac{AB.AC}{2}\ge\dfrac{BE.AC}{2}=\dfrac{AH.BC}{2}\)

\(\Rightarrow AB.AC\ge AH.BC\left(đpcm\right)\)

Dấu bằng xảy ra khi và chỉ khi : BE trùng với AB

\(\Leftrightarrow\Delta ABC\) vuông tại A .

ĐKXĐ : \(x\ge\dfrac{1}{2}\)

Đặt \(\sqrt{2x-1}=a;\sqrt{8x+1}=b\left(a;b\ge0\right)\)

=> \(a^2=2x-1;b^2=8x+1\Rightarrow\dfrac{a^2+b^2}{10}=x\)

Lại có \((13x+1).\sqrt{2x-1}=(7x-1).\sqrt{8x+1}-4\)

\(\Leftrightarrow-\left(\sqrt{2x-1}\right)^3+15x.\sqrt{2x-1}=-\left(\sqrt{8x+1}\right)^3+15x.\sqrt{8x+1}-4\)

\(\Leftrightarrow-a^3+15ax=-b^3+15bx-4\)

\(\Leftrightarrow a^3-b^3-\dfrac{3}{2}.\left(a-b\right).\left(a^2+b^2\right)=4\)

\(\Leftrightarrow-\left(a-b\right)^3=8\)

\(\Leftrightarrow a=b-2\)

Thay vào ta được : \(\sqrt{2x-1}=\sqrt{8x+1}-2\)

\(\Leftrightarrow3x+3=2\sqrt{8x+1}\) 

\(\Leftrightarrow\left\{{}\begin{matrix}9x^2-14x+5=0\\x\ge-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{5}{9}\end{matrix}\right.\)(tm ĐKXĐ)

√4−√7−√4+√7+√7=√2(√4−√7−√4+√7+√7)√2=√8−2√7−√8+2√7+√14√2=√7−2√7+1−√7+2√7+1+√14√2=√(√7−1)2−√(√7+1)2+√14√2=∣∣√7−1∣∣−∣∣√7+1∣∣+√14√2=√7−1−√7−1+√14√2=√14−2√2=√2(√7−√2)√2=√7−√2

Lời giải:
\(\sqrt{4-\sqrt{7}}-\sqrt{4+\sqrt{7}}=\sqrt{\frac{8-2\sqrt{7}}{2}}-\sqrt{\frac{8+2\sqrt{7}}{2}}=\sqrt{\frac{(\sqrt{7}-1)^2}{2}}-\sqrt{\frac{(\sqrt{7}+1)^2}{2}}\)

\(=\frac{|\sqrt{7}-1|}{\sqrt{2}}-\frac{|\sqrt{7}+1|}{\sqrt{2}}=\frac{\sqrt{7}-1-(\sqrt{7}+1)}{\sqrt{2}}=\frac{-2}{\sqrt{2}}=-\sqrt{2}\)