a: Vì AB+BC=AC

nên B nằm giữa A và C

b: M nằm giữa B và C

=>MC+MB=BC

=>MB+1=4

=>MB=3(cm)

Vì BA và BC là hai tia đối nhau

nên BA và BM là hai tia đối nhau

=>B nằm giữa A và M

mà BA=BM(=3cm)

nên B là trung điểm của AM

=>\(AM=2\cdot AB=6\left(cm\right)\)

\(A=\left(\dfrac{1}{2}+1\right)\left(\dfrac{1}{3}+1\right)\cdot...\left(\dfrac{1}{99}+1\right)\)

\(=\dfrac{3}{2}\cdot\dfrac{4}{3}\cdot...\cdot\dfrac{100}{99}\)

\(=\dfrac{100}{2}=50\)

\(B=\left(\dfrac{1}{2}-1\right)\left(\dfrac{1}{3}-1\right)\cdot...\left(\dfrac{1}{100}-1\right)\)

\(=\dfrac{-1}{2}\cdot\dfrac{-2}{3}\cdot...\cdot\dfrac{-99}{100}\)

\(=-\dfrac{1}{100}\)

\(C=\dfrac{3}{2^2}\cdot\dfrac{8}{3^2}\cdot...\cdot\dfrac{899}{30^2}\)

\(=\dfrac{1\cdot3}{2\cdot2}\cdot\dfrac{2\cdot4}{3\cdot3}\cdot...\cdot\dfrac{29\cdot31}{30\cdot30}\)

\(=\dfrac{1\cdot2\cdot3\cdot...\cdot29}{2\cdot3\cdot...\cdot30}\cdot\dfrac{3\cdot4\cdot...\cdot31}{2\cdot3\cdot...\cdot30}\)

\(=\dfrac{1}{30}\cdot\dfrac{31}{2}=\dfrac{31}{60}\)

\(D=\dfrac{3}{1\cdot2}+\dfrac{3}{2\cdot3}+...+\dfrac{3}{99\cdot100}\)

\(=3\left(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{99\cdot100}\right)\)

\(=3\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{99}-\dfrac{1}{100}\right)\)

\(=3\left(1-\dfrac{1}{100}\right)=3\cdot\dfrac{99}{100}=\dfrac{297}{100}\)

\(E=\dfrac{\dfrac{1}{9}-\dfrac{5}{6}-4}{\dfrac{7}{12}-\dfrac{1}{36}-10}=\dfrac{2-15-72}{18}:\dfrac{21-1-360}{36}\)

\(=\dfrac{-85}{18}\cdot\dfrac{36}{-340}=\dfrac{36}{18}\cdot\dfrac{85}{340}=\dfrac{2}{4}=\dfrac{1}{2}\)

-9,12>-9,7 nha 

Vì 9,12 < 9,7

Nên 9,12 x (-1) > 9,7 x (-1)

       -9,12 > - 9,7

Khi nhân cả hai vế của bất đẳng thức với cùng một số âm thì bất đẳng thức đổi chiều.

theo đề ta có

a-3⋮5

a-4⋮7            (a nhỏ nhất)

=>

a-3+20⋮5

a-4+21⋮7

=>a+17⋮5

    a+17⋮7

=>a+17 E BCNN(5,7)=35

=>a=35-17=18

a chia 5 dư 3 nên \(a-3\in B\left(5\right)\)

=>\(a-3\in\left\{0;5;10;15;20;...\right\}\)

=>\(a\in\left\{3;8;13;18;23;...\right\}\left(1\right)\)

a chia 7 dư 4 nên \(a-4\in B\left(7\right)\)

=>\(a-4\in\left\{0;7;14;21;...\right\}\)

=>\(a\in\left\{4;11;18;25;...\right\}\left(2\right)\)

Từ (1),(2) suy ra \(\left\{{}\begin{matrix}a\in\left\{3;8;13;18;23;...\right\}\\a\in\left\{4;11;18;25;...\right\}\end{matrix}\right.\)

mà a nhỏ nhất

nên a=18

Câu 12:

a:n tia chung gốc sẽ có \(\dfrac{n\left(n-1\right)}{2}\)(góc)

Theo đề, ta có: \(\dfrac{n\left(n-1\right)}{2}=28\)

=>\(n^2-n=56\)

=>\(n^2-n-56=0\)

=>(n-8)(n+7)=0

=>\(\left[{}\begin{matrix}n=8\left(nhận\right)\\n=-7\left(loại\right)\end{matrix}\right.\)

b: Theo đề, ta có: \(\dfrac{n\left(n-1\right)}{2}=190\)

=>n(n-1)=380

=>\(n^2-n-380=0\)

=>(n-20)(n+19)=0

=>\(\left[{}\begin{matrix}n=20\left(nhận\right)\\n=-19\left(loại\right)\end{matrix}\right.\)

Câu 10:

a: \(\widehat{ABC}< \widehat{BAC}< \widehat{ACB}\)

b: \(\widehat{ABC}+\widehat{BAC}+\widehat{ACB}=180^0\)

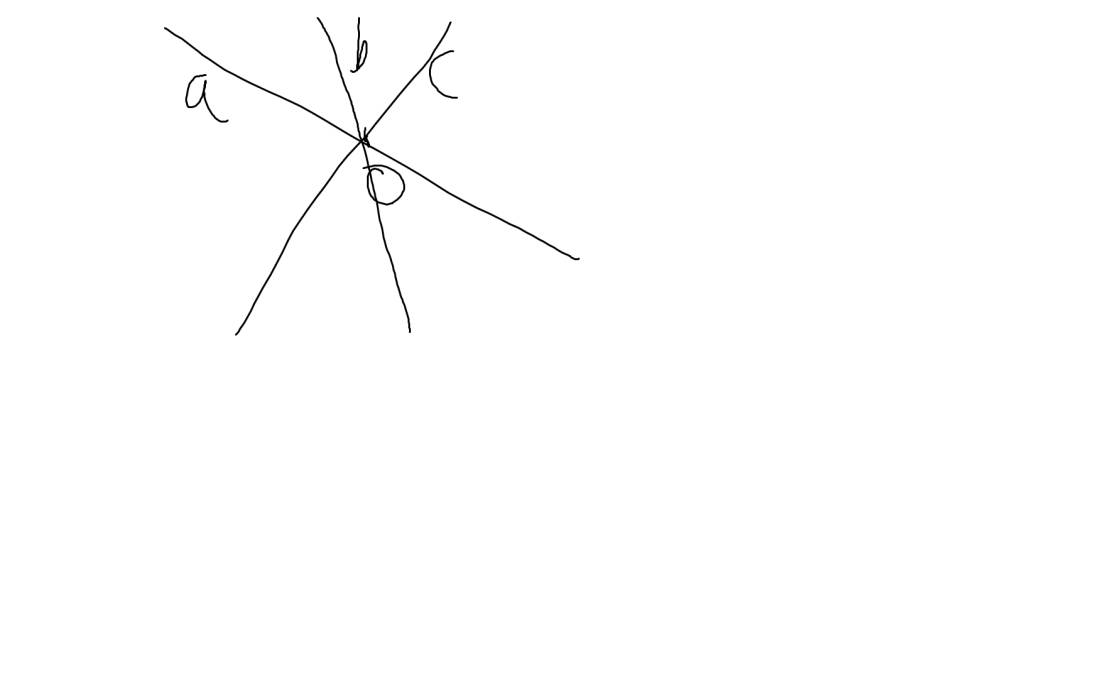
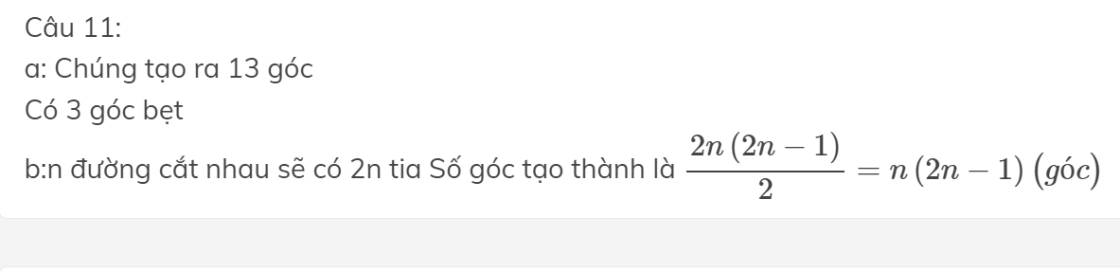
Câu 11:

a: Chúng tạo ra 13 góc

Có 3 góc bẹt

b:n đường cắt nhau sẽ có 2n tia Số góc tạo thành là \(\dfrac{2n\left(2n-1\right)}{2}=n\left(2n-1\right)\left(góc\right)\)

Câu 9:

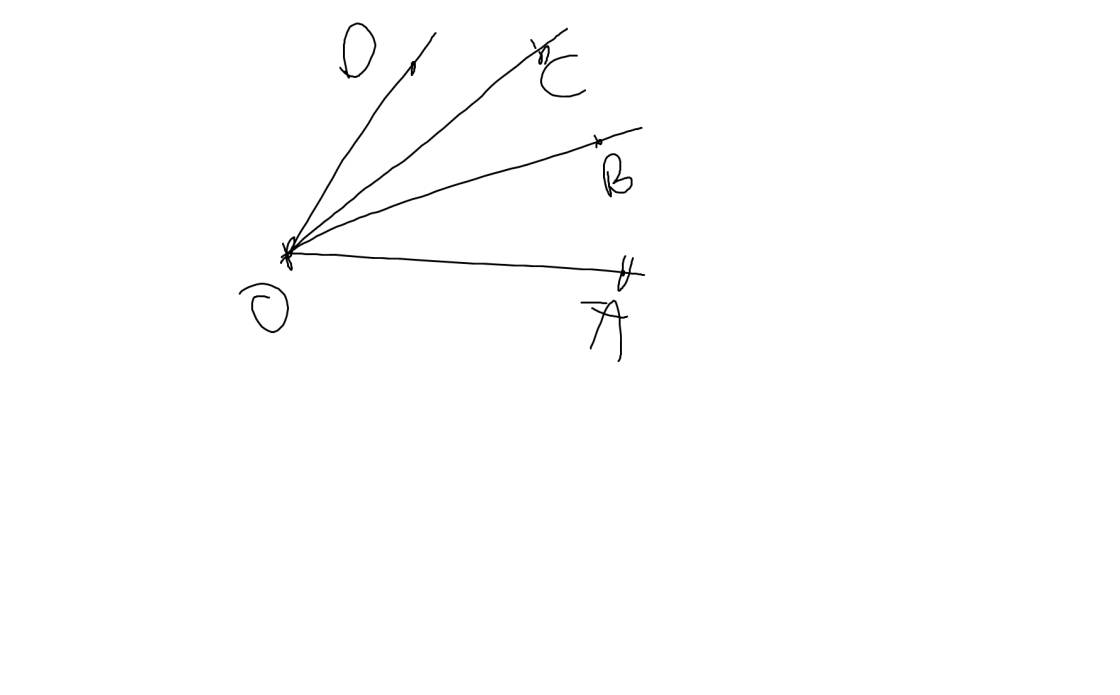
Trên hình vẽ có 6 góc: \(\widehat{AOB};\widehat{AOC};\widehat{AOD};\widehat{BOC};\widehat{BOD};\widehat{COD}\)

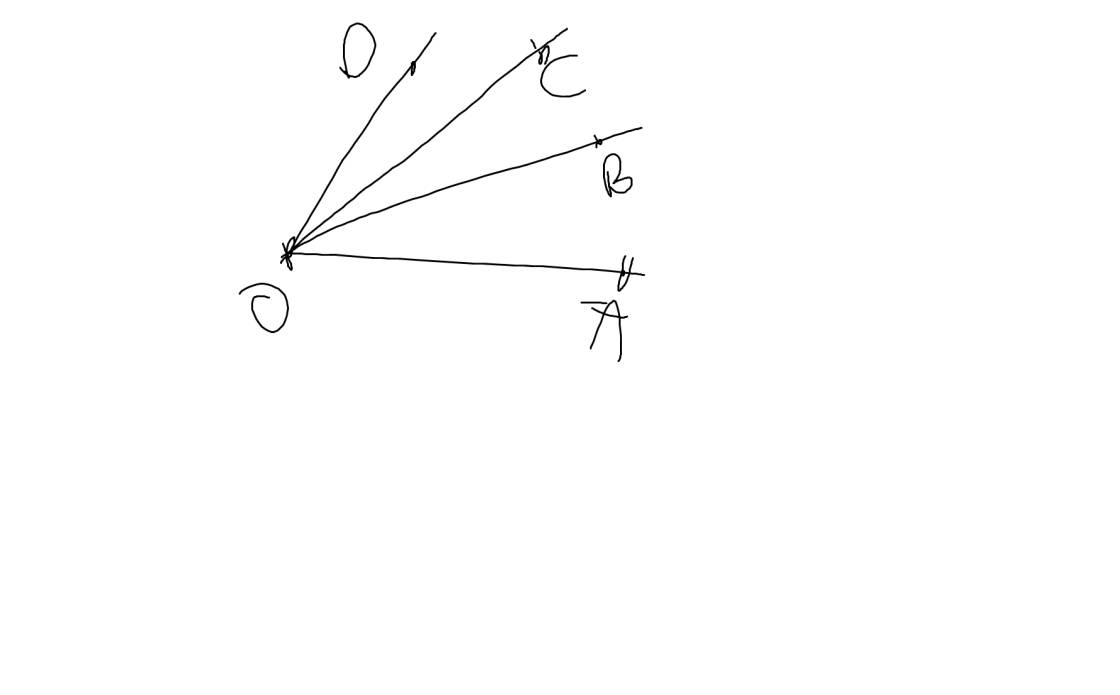
Câu 9:

Trên hình vẽ có 6 góc: \(\widehat{AOB};\widehat{AOC};\widehat{AOD};\widehat{BOC};\widehat{BOD};\widehat{COD}\)

Câu 11:

xy+2y-8=4x+35

=>xy+2y-4x=43

=>y(x+2)-4x-8=35

=>(x+2)(y-4)=35

=>\(\left(x+2\right)\left(y-4\right)=1\cdot35=35\cdot1=\left(-1\right)\cdot\left(-35\right)=\left(-35\right)\cdot\left(-1\right)=5\cdot7=7\cdot5=\left(-5\right)\cdot\left(-7\right)=\left(-7\right)\cdot\left(-5\right)\)

=>\(\left(x+2;y-4\right)\in\left\{\left(1;35\right);\left(35;1\right);\left(-1;-35\right);\left(-35;-1\right);\left(5;7\right);\left(7;5\right);\left(-5;-7\right);\left(-7;-5\right)\right\}\)

=>\(\left(x;y\right)\in\left\{\left(-1;39\right);\left(33;5\right);\left(-3;-31\right);\left(-37;3\right);\left(3;11\right);\left(5;9\right);\left(-7;-3\right);\left(-9;-1\right)\right\}\)

\(10A=\dfrac{10^{2022}+10}{10^{2022}+1}=1+\dfrac{9}{10^{2022}+1}\)

\(10B=\dfrac{10^{2023}+10}{10^{2023}+1}=1+\dfrac{9}{10^{2023}+1}\)

Ta có: \(10^{2022}+1< 10^{2023}+1\)

=>\(\dfrac{9}{10^{2022}+1}>\dfrac{9}{10^{2023}+1}\)

=>\(1+\dfrac{9}{10^{2022}+1}>1+\dfrac{9}{10^{2023}+1}\)

=>10A>10B

=>A>B