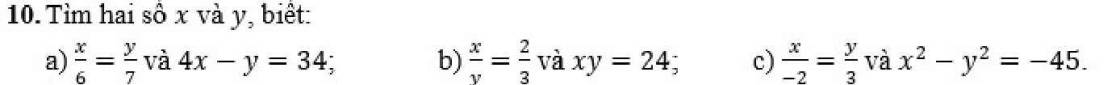
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


KV
25 tháng 11 2023
 a) Xét ∆ABM và ∆CDM có:
a) Xét ∆ABM và ∆CDM có:
AM = CM (gt)
AMB = CMD (đối đỉnh)
BM = DM (gt)
⇒ ∆ABM = ∆CDM (c-g-c)
b) Do ∆ABM = ∆CDM (cmt)
⇒ MAB = MCD (hai góc tương ứng)
⇒ MCD = 90⁰
⇒ MC ⊥ CD
⇒ AC ⊥ CD

AH
Akai Haruma
Giáo viên
24 tháng 11 2023
Lời giải:
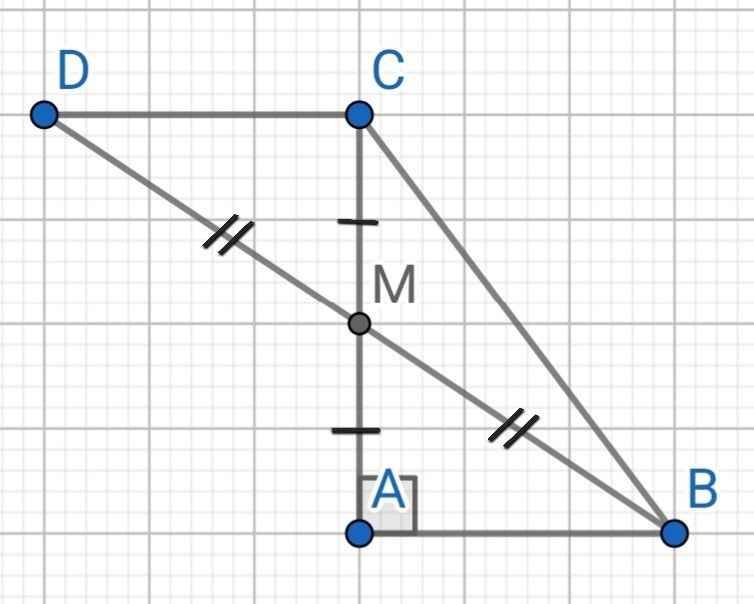
Xét tam giác $ABM$ và $ACM$ có:
$AB=AC$
$\widehat{BAM}=\widehat{CAM}$ (do $AM$ là tia phân giác $\widehat{A}$)
$AM$ chung
$\Rightarrow \triangle ABM=\triangle ACM$ (c.g.c)
$\Rightarrow BM=CM$
TT
0

a) \(\dfrac{x}{6}=\dfrac{y}{7}\Rightarrow\dfrac{4x}{24}=\dfrac{y}{7}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{4x}{24}=\dfrac{y}{7}=\dfrac{4x-y}{24-7}=\dfrac{34}{17}=2\)
\(\dfrac{x}{6}=2\Rightarrow x=2.6=12\)
\(\dfrac{y}{7}=2\Rightarrow y=2.7=14\)
Vậy \(x=12;y=14\)
b) \(\dfrac{x}{y}=\dfrac{2}{3}\Rightarrow x=\dfrac{2}{3}y\)
Thay \(x=\dfrac{2}{3}y\) vào \(xy=24\) ta có:
\(\dfrac{2}{3}y.y=24\)
\(\Rightarrow y^2=24:\dfrac{2}{3}=36\)
\(\Rightarrow y=6;y=-6\)
*) \(y=6\Rightarrow x=\dfrac{2}{3}.6=4\)
*) \(y=-6\Rightarrow x=\dfrac{2}{3}.\left(-6\right)=-4\)
Vậy \(x=4;y=6\)
Hoặc \(x=-4;y=-6\)
c) \(\dfrac{x}{-2}=\dfrac{y}{3}\Rightarrow\dfrac{x^2}{4}=\dfrac{y^2}{9}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{x^2}{4}=\dfrac{y^2}{9}=\dfrac{x^2-y^2}{4-9}=\dfrac{-45}{-5}=9\)
*) \(\dfrac{x^2}{4}=9\Rightarrow x^2=4.9=36\)
\(\Rightarrow x=6;x=-6\)
Với \(x=6\Rightarrow y=\dfrac{6}{-2}.3=-9\)
Với \(x=-6\Rightarrow y=\dfrac{-6}{-2}.3=9\)
Vậy \(x=6;y=-9\)
Hoặc \(x=-6;y=9\)