Ta có: \(n_{Mg}=\dfrac{2,4}{24}=0,1\left(mol\right)\)

PT: \(Mg+2HCl\rightarrow MgCl_2+H_2\)

Theo PT: \(n_{MgCl_2}=n_{H_2}=n_{Mg}=0,1\left(mol\right)\)

a, \(m_{MgCl_2}=0,1.95=9,5\left(g\right)\)

b, \(V_{H_2}=0,1.24,79=2,479\left(l\right)\)

c, \(n_{HCl}=2n_{Mg}=0,2\left(mol\right)\)

\(\Rightarrow m_{ddHCl}=\dfrac{0,2.36,5}{3,65\%}=200\left(g\right)\)

Bài `1`

\(a,5x^2-10xy=5x\left(x-2y\right)\\ b,3x\left(x-y\right)-6\left(x-y\right)=\left(x-y\right)\left(3x-6\right)\\ =3\left(x-y\right)\left(x-2\right)\\ c,2x\left(x-y\right)-4y\left(y-x\right)=2x\left(x-y\right)+4y\left(x-y\right)\\ =\left(x-y\right)\left(2x+4y\right)=2\left(x-y\right)\left(x+2y\right)\\ d,9x^2-9y^2=\left(3x\right)^2-\left(3y\right)^2=\left(3x-3y\right)\left(3x+3y\right)\\ f,xy-xz-y+z=\left(xy-xz\right)-\left(y-z\right)\\ =x\left(y-z\right)-\left(y-z\right)=\left(y-z\right)\left(x-1\right)\)

Bài `3`

\(a,3x^2+8x=0\\ \Leftrightarrow x\left(3x+8\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\3x+8=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\3x=-8\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{8}{3}\end{matrix}\right.\)

\(b,9x^2-25=0\\ \Leftrightarrow\left(3x\right)^2-5^2=0\\ \Leftrightarrow\left(3x-5\right)\left(3x+5\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}3x-5=0\\3x+5=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}3x=5\\3x=-5\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{3}\\x=-\dfrac{5}{3}\end{matrix}\right.\)

\(c,x^3-16x=0\\ \Leftrightarrow x\left(x^2-16\right)=0\\ \Leftrightarrow x\left(x-4\right)\left(x+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x-4=0\\x+4=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\\x=-4\end{matrix}\right.\)

\(d,x^3+x=0\\ \Leftrightarrow x\left(x^2+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x^2+1\in\varnothing\\x=0\end{matrix}\right.\Rightarrow x=0\)

a) (a - 2b)x(a + 2b)
b) x²-(y-3)²
 => (x-y+3)(x+y-3)
c) (2a + b - a)(2a + b + a)
=> (a+b)(3a+b)
d) (4(x - 1))² - (5(x + y))²
⇔ (4x - 4 - 5x - 5y)(4x - 4 + 5x + 5y)
⇔ -(x + 5y + 4)(9x + 5y + -4)
e) (x + 5)²
f) (5x - 2y)²
h) (x - 5)(x² + 5x + 25)

k) (x + 5)³

Ta có: \(n_{HCl}=0,2.1=0,2\left(mol\right)\)

\(n_{NaOH}=0,3.2=0,6\left(mol\right)\)

PT: \(HCl+NaOH\rightarrow NaCl+H_2O\)

Xét tỉ lệ: \(\dfrac{0,2}{1}< \dfrac{0,6}{1}\), ta được NaOH dư.

Theo PT: \(n_{NaOH\left(pư\right)}=n_{HCl}=0,2\left(mol\right)\)

\(\Rightarrow n_{NaOH\left(dư\right)}=0,6-0,2=0,4\left(mol\right)\)

\(\Rightarrow m_{NaOH\left(dư\right)}=0,4.40=16\left(g\right)\)

- Quỳ tím hóa xanh do NaOH dư.

Lời giải:
a. Xét tứ giác $ADHE$ có 3 góc vuông $\widehat{A}=\widehat{D}=\widehat{E}=90^0$ nên tứ giác $ADHE$ là hình chữ nhật.

b.

Xét tam giác vuông $BDH$ vuông tại $D$ có $DI$ là đường trung tuyến ứng với cạnh huyền $BH$ nên $DI=\frac{BH}{2}=IH$

$\Rightarrow DIH$ là tam giác vuông tại $I$

$\Rightarrow \widehat{IDH}=\widehat{IHD}$ (1)

$ADHE$ là hình chữ nhật nên $\widehat{HDE}=\widehat{HAE}=\widehat{HAC}$ (2)

Từ $(1); (2)\Rightarrow \widehat{IDH}+\widehat{HDE}=\widehat{IHD}+\widehat{HAC}$

$\Rightarrow \widehat{IDE}=\widehat{IHD}+\widehat{HAC}$.

Mà $\widehat{IHD}=\widehat{HCA}$ (2 góc đồng vị)

$\Rightarrow \widehat{IDE}=\widehat{HCA}+\widehat{HAC}=180^0-\widehat{AHC}=180^0-90^0=90^0$

$\Rightarrow DI\perp DE$

c. Tương tự phần a ta suy ra $DE\perp EK$

Vậy $DI\perp DE, EK\perp DE$

$\Rightarrow DI\parallel EK$ và $DI, EK$ cùng vuông góc với $DE$

$\Rightarrow DIKE$ là hình thang vuông.

d.

Có: $DI=\frac{BH}{2}\Rightarrow BH=2DI=2.1=2$ (cm) 

$EK=\frac{CH}{2}\Rightarrow CH=2EK=8$ (cm)

$\Rightarrow BC=BH+CH=2+8=10$ (cm)

$S_{ABC}=AH.BC:2=6.10:2=30$ (cm²)

Hình vẽ:

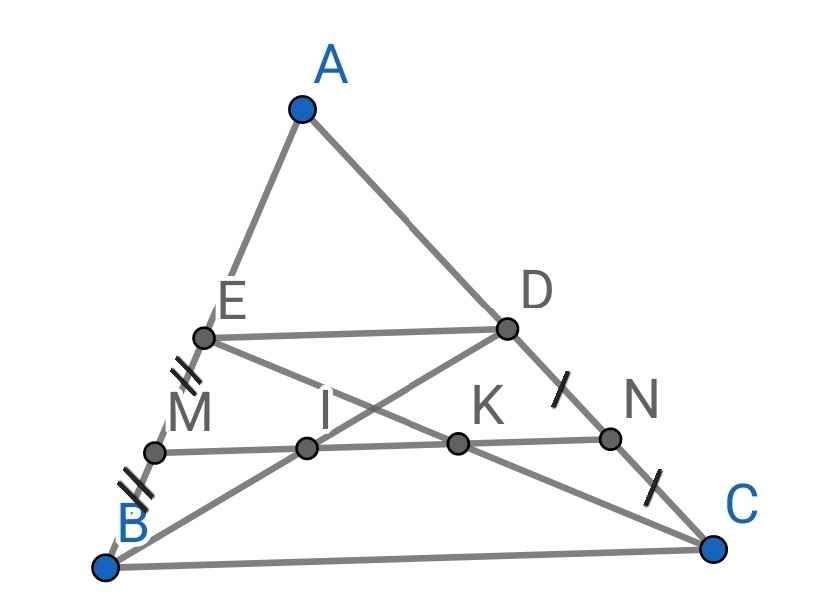
Do BD là đường trung tuyến của ∆ABC (gt)

⇒ D là trung điểm của AC

Do CE là đường trung tuyến của ∆ABC (gt)

⇒ E là trung điểm của AB

⇒ DE là đường trung bình của ∆ABC

⇒ DE // BC và DE = BC : 2

⇒ BC = 2DE

Do DE // BC (cmt)

⇒ BCDE là hình thang

Do M là trung điểm của BE (gt)

N là trung điểm của CD (gt)

⇒ MN là đường trung bình của hình thang BCDE

⇒ MN // DE // BC và MN = (DE + BC) : 2

Do MN // DE (cmt)

⇒ MI // DE và NK // DE

∆BDE có:

MI // DE (cmt)

M là trung điểm của BE (gt)

⇒ I là trung điểm của BD

⇒ MI là đường trung bình của ∆BDE

⇒ MI = DE : 2   (1)

∆CDE có:

NK // DE (cmt)

N là trung điểm của CD (gt)

⇒ K là trung điểm của CE

⇒ NK là đường trung bình của ∆CDE

⇒ NK = DE : 2   (2)

Mà MI = DE : 2

⇒ MI = NK = DE : 2

⇒ MI + NK = DE

Ta có:

MN = (DE + BC) : 2

Mà BC = 2DE (cmt)

⇒ MN = (DE + 2DE) : 2

= DE + DE : 2

Lại có:

MN = MI + IK + NK

= (MI + NK) + IK

= DE + IK

⇒ DE + IK = DE + DE : 2

⇒ IK = DE : 2 (3)

Từ (1), (2) và (3) ⇒ MI = IK = KN

Xét $\Delta BED$ có {��//����=��{​MI//EDME=BM​ suy ra $ID=IB$.

Xét $\Delta CED$ có {��//����=��{​NK//EDNC=ND​ suy ra $KE=KC$.

Suy ra ��=12��MI=21​ED; ��=12��NK=21​ED; ��=12��ED=21​BC.

��=��−��=12��−12��=��−12��=12��IK=MK−MI=21​BC−21​DE=DE−21​DE=21​DE.

Vậy $MI=IK=KN$.

A B C M N G D E

a/

Xét tg ABC có

NA=NB; MA=MC => MN là đường trung bình của tg ABC => MN//BC

Xét tg GBC có

DG=DB; EG=EC => DE là đường trung bình của tg GBC => DE//BC

=> MN//DE (cùng // BC)

b/

Xét tg ABG có

NA=NB; DG=DB => ND là đường trung bình của tg ABG => ND//AG

Xét tg ACG có

MA=MC; EG=EC => ME là đường trung bình của tg ACG => ME//AG

=> ND//ME (cùng // với AG)

a) Vì $BM$, $CN$ là các đường trung tuyến của $\Delta ABC$ nên $MA=MC$, $NA=NB$.

Do đó $MN$ là đường trung bình của $\Delta ABC$, suy ra $MN$ // $BC$. (1)

Ta có $DE$ là đường trung bình của $\Delta GBC$ nên $DE$ // $BC$.  (2)

Từ (1) và (2) suy ra $MN$ // $DE$.

b) Xét $\Delta ABG$, ta có $ND$ là đường trung bình.

Xét $\Delta ACG$, ta có $ME$ là đường trung bình.

Do đó $ND$ // $AG$, $ME$ // $AG$.

Suy ra $ND$ // $ME$.

A B C D M O E

a/ Goi E là trung điểm của MC

Từ gt \(AM=\dfrac{1}{2}MC\Rightarrow AM=ME=EC\)

Xét tg BCM có

ME=EC (cmt); DB=DC (gt) => DE là đường trung bình của tg BCM

=> DE//BM 

Xét tg ADE có

AM=ME (cmt)

BM//DE (cmt) =>OM//DE

=> OA=OD (trong tg đường thẳng đi qua trung điểm của 1 cạnh và // với 1 cạnh thì đi qua trung điểm cạnh còn lại)

b/

Ta có DE là đường trung bình của tg BCM \(\Rightarrow DE=\dfrac{1}{2}BM\)

Xét tg ADE có

OA=OD (cmt); AM=ME (cmt) => OM là đường trung bình của tg ADE

\(\Rightarrow OM=\dfrac{1}{2}DE=\dfrac{1}{2}.\dfrac{1}{2}BM=\dfrac{1}{4}BM\)

a) Qua $D$ vẽ một đường thẳng song song với $BM$ cắt $AC$ tại $N$.

Xét $\Delta MBC$ có $DB=DC$ và $DN$ // $BM$ nên ��=��=12��MN=NC=21​MC (định lí đường trung bình của tam giác).

Mặt khác ��=12��AM=21​MC, do đó ��=��=12��AM=MN=21​MC.

Xét $\Delta AND$ có $AM=MN$ và $BM$ // $DN$ nên $OA=OD$ hay $O$ là trung điểm của $AD$.

b) Xét $\Delta AND$ có $OM$ là đường trung bình nên ��=12��OM=21​DN. (1)

Xét $\Delta MBC$ có $DN$ là đường trung bình nên ��=12��DN=21​BM. (2)

Từ (1) và (2) suy ra ��=14��OM=41​BM.