trong buổi tham quan bên công viên cây xanh Em và các bạn đã quan sát đc các đv sau con ong. con cóc, con thằn lằn , con giun đất, con chim. hãy vẽ sơ đồ khóa lưỡng phân chia các đv trên
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tổng số điểm trên đoạn thẳng AB là 2023+2=2025(điểm)
Số cách lấy 2 điểm trong 2025 điểm là \(C^2_{2025}\left(cách\right)\)
=>Số tam giác tạo thành là \(C^2_{2025}\)(tam giác)

a: Xét tứ gíc AMDN có \(\widehat{AMD}=\widehat{AND}=\widehat{MAN}=90^0\)
nên AMDN là hình chữ nhật
=>AD=MN
b: Xét ΔHBA vuông tại H và ΔHAC vuông tại H có
\(\widehat{HBA}=\widehat{HAC}\left(=90^0-\widehat{HCA}\right)\)
Do đó: ΔHBA~ΔHAC
=>\(\dfrac{HB}{HA}=\dfrac{HA}{HC}\)
=>\(HA^2=HB\cdot HC\)
c: \(HA^2=HB\cdot HC\)
=>\(HA^2=2\cdot8=16=4^2\)
=>HA=4(cm)
ΔHAB vuông tại H
=>\(HA^2+HB^2=AB^2\)
=>\(AB=\sqrt{4^2+2^2}=2\sqrt{5}\left(cm\right)\)
ΔHAC vuông tại H
=>\(HA^2+HC^2=AC^2\)
=>\(AC=\sqrt{4^2+8^2}=4\sqrt{5}\left(cm\right)\)


C nằm giữa A và B
=>CA+CB=AB
=>CB+2=7
=>CB=5(cm)
D là trung điểm của AC
=>\(AD=DC=\dfrac{AC}{2}=\dfrac{2}{2}=1\left(cm\right)\)
E là trung điểm của CB
=>\(EC=EB=\dfrac{BC}{2}=2,5\left(cm\right)\)
CA và CB là hai tia đối nhau
=>CD và CE là hai tia đối nhau
=>C nằm giữa D và E
=>DE=DC+CE=2,5+1=3,5(cm)
F là trung điểm của DE
=>\(DF=\dfrac{DE}{2}=1,75\left(cm\right)\)
Vì DC<DF
nên C nằm giữa D và F
=>DC+CF=DF
=>CF+1=1,75
=>CF=0,75(cm)

a: a: Xét ΔABC và ΔAED có
\(\dfrac{AB}{AE}=\dfrac{AC}{AD}\left(\dfrac{15}{5}=\dfrac{21}{7}=3\right)\)
\(\widehat{BAC}\) chung
Do đó: ΔABC~ΔAED
Vì \(\dfrac{AB}{AE}=\dfrac{AC}{AD}\)
nên \(AB\cdot AD=AE\cdot AC\)
b: \(\dfrac{AB}{AE}=\dfrac{AC}{AD}\)
=>\(\dfrac{AB}{AC}=\dfrac{AE}{AD}\)
Xét ΔABE và ΔACD có
\(\dfrac{AB}{AC}=\dfrac{AE}{AD}\)
\(\widehat{BAE}\) chung
Do đó: ΔABE~ΔACD
=>\(\widehat{ABE}=\widehat{ACD};\widehat{AEB}=\widehat{ADC}\)
c: Xét ΔOBD và ΔOCE có
\(\widehat{OBD}=\widehat{OCE}\)
\(\widehat{BOD}=\widehat{COE}\)(hai góc đối đỉnh)
Do đó: ΔOBD~ΔOCE
=>\(\dfrac{OB}{OC}=\dfrac{OD}{OE}\)
=>\(OB\cdot OE=OD\cdot OC\)

Lời giải:
\(B=(\frac{1}{101}+\frac{1}{102}+...+\frac{1}{120})+(\frac{1}{121}+...+\frac{1}{140})+(\frac{1}{141}+....+\frac{1}{160})+(\frac{1}{161}+...+\frac{1}{180})+(\frac{1}{181}+...+\frac{1}{200})\)
\(> \frac{20}{120}+\frac{20}{140}+\frac{20}{160}+\frac{20}{180}+\frac{20}{200}=\frac{1627}{2520}> \frac{5}{8}\)

1 haven't played - has been
2 Have you chosen - bought
3 has forgot - didn't say
4 Have you sold - saw - bought
5 have lost - ran
6 has stopped
7 has changed
8 have forgot
9 arrested
10 has improved

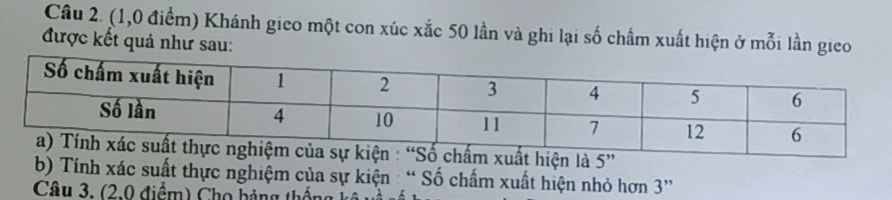
a: Gọi A là biến cố "Số chấm xuất hiện là 5"
=>n(A)=12
=>Xác suất thực nghiệm là \(P_A=\dfrac{12}{50}=0,24\)
b: Gọi B là biến cố "Số chấm xuất hiện nhỏ hơn 3"
=>n(B)=4+10=14
=>Xác suất thực nghiệm là \(P_B=\dfrac{14}{50}=0,28\)

Đáp án:
Giải thích các bước giải:
Dưới đây là sơ đồ khóa lưỡng phân của các đơn vị (đv) bạn đã đề cập:
Độngvật Gainhím Chim Conong Concóc | | Conthằn CongiunđấtĐộ𝑛𝑔𝑣ậ𝑡 𝐺𝑎𝑖𝑛ℎí𝑚 𝐶ℎ𝑖𝑚 𝐶𝑜𝑛𝑜𝑛𝑔 𝐶𝑜𝑛𝑐ó𝑐 | | 𝐶𝑜𝑛𝑡ℎằ𝑛 𝐶𝑜𝑛𝑔𝑖𝑢𝑛đấ𝑡
Trong sơ đồ trên, "Động vật" là cấp độ cao nhất, sau đó chia thành hai nhánh là "Gai nhím" và "Chim". "Gai nhím" tiếp tục phân nhánh thành "Con ong" và "Con cóc". Trong khi đó, "Chim" là một nhánh riêng và không có sự phân nhánh khác. "Con ong" lại chia thành "Con thằn lằn" và "Con giun đất".
Sơ đồ này giúp minh họa cách mà các đơn vị động vật được phân chia và hệ thống hóa.
>